Guest 018946
Επισκέπτης


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Athr
Εκκολαπτόμενο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 018946
Επισκέπτης


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Athr
Εκκολαπτόμενο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 018946
Επισκέπτης


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
13diagoras
Δραστήριο μέλος


θα ηταν καλο να μαζευουμε την θεωρια που χρησιμοποιουμε στις πιο προχωρημενες ασκησεις και καποιος να την γραψει σε pdf για να εχουν ολοι οι μαθητες μια ιδεα για λιγο πιο προωρημενα πραγματα
εστω οτι θελω να αποδειξω την ανισοτηταμε :
και :
μπορω να πω πως
,
 )
τοτε προσθετω τις (1) , (2) και (3) κατα μελη και προκυπτει το ζητουμενο. Η μεθοδος αυτη ισχυει ή ειναι λαθος ?
Φιλε Τασο,ΑΝ καταλαβα καλα αυτος ο ισχυρισμος δεν ευσταθει.Αν παρουμε την σχεση με το a ,τοτε αφου το a απο την εκφωνιση ειναι θετικος πραγματικος,γινεται η απλοποιηση της ανισοτητας χωρις να αλλαξει η φορα της ,οποτε προκυπτει οτι a>=1 κατι το οποιο δεν αναφερεται στην εκφωνιση.Επισης,δεν χρησιμοποιηθηκε η ισοτητα abc=1 σχεση η οποια πρεπει να αξιοποιηθει στην αποδειξη του ζητουμενου.
Αν και ειμαι "σκουριασμενος" απο τα μαθηματικα λογω Πανελλαδικων(αποτοξινωση
 ) κοιταξα την ασκηση και ελπιζω να μην την απογοητευσα
) κοιταξα την ασκηση και ελπιζω να μην την απογοητευσα
Λοιπον:
Ειναι a²+b²+c²>=(a+b+c)²-2(ab+cb+ac)>=(a+b+c)² (1),αφου a,b,c θετικοι,αρα και ab+ac+cb>0
Επισης a+b+c>=1(2),διοτι εστω οτι δεν ισχυει,τοτε a+b+c<1,οποτε και a<1 και b<1 και c<1(a,b,c, θετικοι,αλλιως δεν ισχυει αυτο) ατοπο,αφου abc=1.
Ετσι απο την 1,2<=> a²+b²+c²>=(a+b+c)* η ισοτητα αν και μονο αν a=1,b=1,c=1
*Αν x>1,τοτε χ²>χ.Για αποδειξη φερνεις το χ στο πρωτο μελος ,βγαζεις κοινο παραγοντα,απαλοιφεις το χ αφου ειναι θετικο(χ>1)και μενει χ>1 κατι τ οποιο ισχυει απο την υποθεση.
Αυτα

edit:Απροσεξια στα κοκκινισμενα.Λαθος λυση

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
BILL KEXA
Νεοφερμένο μέλος
Bl4Ck_PyTh0N!
Δραστήριο μέλος


dr.tasos δοκίμασα να λύσω αυτή την πολυωνυμική εξίσωση ...... Έτσι λύνεται ???
Σωστή είναι η λύση σου.Μπράβο!

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
papas
Διάσημο μέλος


x^2=i^2
x=+i ή x=-i
x^4=-1 (παλι τα ιδια στους μιγαδικους : i^2=-1,οπου i η φανταστικη μοναδα)
χ^4=i^2
x^4-i^2=0
(x^2-i)(x^2+i)=0
x^2-i=0 ή x^2+i=0
(μετα δεν ξερω την συνεχεια
 )
)Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
ξαροπ
Πολύ δραστήριο μέλος


Φιλε Τασο,ΑΝ καταλαβα καλα αυτος ο ισχυρισμος δεν ευσταθει.Αν παρουμε την σχεση με το a ,τοτε αφου το a απο την εκφωνιση ειναι θετικος πραγματικος,τοτε γινεται η απλοποιηση της ανισοτητας χωρις να αλλαξει η φορα της ,οποτε προκυπτει οτι a>=1 κατι το οποιο δεν αναφερεται στην εκφωνιση.Επισης,δεν χρησιμοποιηθηκε η ισοτητα abc=1 σχεση η οποια πρεπει να αξιοποιηθει στην αποδειξη του ζητουμενου.
Αν και ειμαι "σκουριασμενος" απο τα μαθηματικα λογω Πανελλαδικων(αποτοξινωση) κοιταξα την ασκηση και ελπιζω να μην την απογοητευσα
Λοιπον:
Ειναι a²+b²+c²>=(a+b+c)²-2(ab+cb+ac)>=(a+b+c)² (1),αφου a,b,c θετικοι,αρα και ab+ac+cb>0
Επισης a+b+c>=1(2),διοτι εστω οτι δεν ισχυει,τοτε a+b+c<1,οποτε και a<1 και b<1 και c<1(a,b,c, θετικοι,αλλιως δεν ισχυει αυτο) ατοπο,αφου abc=1.
Ετσι απο την 1,2<=> a²+b²+c²>=(a+b+c)* η ισοτητα αν και μονο αν a=1,b=1,c=1
*Αν x>1,τοτε χ²>χ.Για αποδειξη φερνεις το χ στο πρωτο μελος ,βγαζεις κοινο παραγοντα,απαλοιφεις το χ αφου ειναι θετικο(χ>1)και μενει χ>1 κατι τ οποιο ισχυει απο την υποθεση.
Αυτα
Diagoras13, η άσκηση δεν λύνεται τόσο απλά (τουλάχιστον όχι με τον τρόπο που έγραψες). Κάποιες παρατηρήσεις (πάνω σε αυτά που γράψατε εσύ και ο dr. tasos)
1. Προφανώς ισχύει
σε καμία περίπτωση όμως δεν ισχύει
με θετικά α,β,γ, αφού προκύπτει
2. Δεν ισχύει απλά
αλλά
από υπόθεση.
3. Αν για θετικούς α,β,γ ισχύει
δεν ισχύει απαραίτητα
για παράδειγμα, αν
τότε έχουμε
ενώ ταυτόχρονα
και
(δηλαδή επαληθεύουν την ανισότητα προς απόδειξη).
Προτού αντιμετωπίσει κανείς την ανισότητα του dr. tasos, καλύτερα να ασχοληθεί με μια παρόμοια ανισότητα δύο μεταβλητών, πχ. να τσεκάρει αν ισχύει για θετικούς α,β με
ότι
(σαν πιο εύκολο θέμα).
Επίσης για τέτοιου είδους ανισότητες 'υπό συνθήκη', βολεύει καμιά φορά να "εξαφανίσουμε" αυτή τη συνθήκη με 'νέες μεταβλητές', και να επιχειρήσουμε να αποδείξουμε μια νέα ανισότητα χωρίς συνθήκη (χωρίς δηλαδή να μας βασανίζει το ερώτημα "πού θα τη χρησιμοποιήσω τη συνθήκη? Πόσες φορές?")
Τι εννοώ:
Η ανισότητα του dr. tasos μπορεί να γίνει ανισότητα δύο μεταβλητών.
Θέτουμε
και έχουμε να αποδείξουμε ότι
με α,β να είναι οποιοιδήποτε θετικοί αριθμοί.
Επίσης, χωρίς να βλάψουμε τη γενικότητα, θεωρούμε
Τότε έχουμε
και η ανισότητα προς απόδειξη γίνεται
χωρίς τα x,y,z να πληρούν κάποια συνθήκη.
Υπάρχουν και άλλοι τρόποι αντιμετώπισης τέτοιων ανισοτήτων, δύο παραδείγματα έφερα απλά. Μπορεί για κάποιον καινούριο σε όλα αυτά να φαντάζουν υπερβολικά δύσκολα και δυσνόητα τα παραπάνω, αλλά όπως είπαμε μιλάμε για ανισότητες σε 'ανώτερο' του σχολικού επίπεδο.
___________________________________________________________________________________________________________
να βρειτε τις πραγματικες ριζες της εξισωσης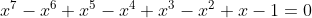
Και μια άλλη λύση...
Παρατηρούμε ότι το
δεν αποτελεί λύση της εξίσωσης, άρα πολλαπλασιάζουμε την εξίσωση με
και προκύπτει
αφού απαιτούμε
Όσες πραγματικές λύσεις έχει η (2), τόσες θα έχει και η αρχική μείον τον περιορισμό που έχουμε βάλει.
Θέτουμε
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
wfgl
Νεοφερμένο μέλος


Για καμμενους :
x^2=-1 (στους μιγαδικους : i^2=-1,οπου i η φανταστικη μοναδα)
x^2=i^2
x=+i ή x=-i
x^4=-1 (παλι τα ιδια στους μιγαδικους : i^2=-1,οπου i η φανταστικη μοναδα)
χ^4=i^2
x^4-i^2=0
(x^2-i)(x^2+i)=0
x^2-i=0 ή x^2+i=0
(μετα δεν ξερω την συνεχεια)
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
13diagoras
Δραστήριο μέλος



Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 018946
Επισκέπτης


Λοιπον :
Αυτο δεν γινεται να μηδενιστει
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
ξαροπ
Πολύ δραστήριο μέλος


Όμως από την ανισότητα Andreescu σε συνδυασμό με την ανισότητα αριθμητικού - γεωμετρικού μέσου έχουμε ότι
άρα η ανισότητα αποδείχτηκε (και μάλιστα δεν χρειάζεται να ισχύει μόνο
αλλά
Επίσης, μια πιο στοιχειώδης απόδειξη μπορεί να δοθεί λαμβάνοντας υπ' όψιν ότι
και συνεχίζοντας κανονικά με ανισότητες των μέσων.
Μου φαίνεται τώρα ότι οι τρόποι αντιμετώπισης που πρότεινα πιο πριν (να κάνουμε τις μεταβλητές από τρεις, δύο / να θέσουμε κατάλληλες μεταβλητές για να 'φύγει' η συνθήκη) μάλλον πιο πολύ δυσκολεύουν τα πράγματα παρά διευκολύνουν.
Ο πρώτος τρόπος θέλει αρκετό πραξολόι, ενώ για το δεύτερο διαβλέπω μια χρήση της ανισότητας της αναδιάταξης αλλά δεν έκατσα κάτω να το δω, οπότε δεν το 'χω και σίγουρο.
Και κάποιες γενικεύσεις πάνω στην ανισότητα (για ν - όρους υψωμένους στο τετράγωνο και στην k-οστή δύναμη), για όποιους ενδιαφερόμενους.
τότε
1)
2)
3)
Οι αποδείξεις είναι εντελώς όμοιες με την αρχική (γίνεται και χρήση της γενικευμένης Andreescu)
Μια πιο δύσκολη άσκηση, πάνω σε αυτό το θέμα, είναι η εξής.
"Αν
ν.δ.ο.
(νομίζω ότι ήταν και η τελευταία-τελευταία άσκηση σε κάποιο από τα βιβλία ανισοτήτων του Στεργίου)
Προτείνω, αν κάποιος θέλει να 'μπει' πιο πολύ στην ιδέα των ανισοτήτων δυσκολότερου επιπέδου, να ασχοληθεί με τις παρακάτω ασκήσεις για αρχή. (είναι και ξεκάθαρα μέσα στα πλαίσια της Α' Λυκείου)
1.
2.
(ενν. α,β,γ πραγματικοί)
Όσοι θέλουν κάτι πιο δύσκολο, έχω δύο ωραίες (και απλές για τους έμπειρους) ανισότητες προς απόδειξη.
(θυμίζει κάτι από την ανισότητα του δρ. τάσου)
2. Αν α,β μη-μηδενικοί πραγματικοί αριθμοί, τότε
Νομίζω ότι και οι δύο ανισότητες είχαν τεθεί παλιότερα σε κάτι βαλκανικούς, πχ. JBMO.
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 018946
Επισκέπτης


Για την 1 πολζω την ανσοτητα με 2 και μου βγαινει αυτο :
που ισχυει αφου ειναι αθροισμα θετικων.
παμε για την 2 τωρα :
αμα κανω πραξεις βγαζω οτι :
που ισχυει οποτε αποδειξαμε το πρωτο μερος της ανσισοτητας παμε για το δευτερο .
με πραξεις καταληγουμε εδω :
πολζω με 2 και βγαζω αυτο :
που ισχυει
λογω μεταβατικης ισχυει και αυτο :
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
vimaproto
Πολύ δραστήριο μέλος



Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Bl4Ck_PyTh0N!
Δραστήριο μέλος


α)
β)
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
red span
Δραστήριο μέλος


Προκυπτει,απο την λεγομενη ανισοτητα της αναδιαταξηςΜια λύση, χωρίς κενά ελπίζω, πάνω στην ανισότητα του δρ. τάσου γιατί έχουν περάσει μέρες από τότε που μπήκε. Τη βάζω σε spoiler γιατί χρησιμοποιώ κάποια 'εργαλεία' άγνωστα για το λύκειο, όχι μόνο για την Α' Λυκείου.
Η ανισότητα γράφεται ισοδύναμα
.
Όμως από την ανισότητα Andreescu σε συνδυασμό με την ανισότητα αριθμητικού - γεωμετρικού μέσου έχουμε ότι
,
άρα η ανισότητα αποδείχτηκε (και μάλιστα δεν χρειάζεται να ισχύει μόνο
,
αλλά
.)
Επίσης, μια πιο στοιχειώδης απόδειξη μπορεί να δοθεί λαμβάνοντας υπ' όψιν ότι
,
και συνεχίζοντας κανονικά με ανισότητες των μέσων.
Μου φαίνεται τώρα ότι οι τρόποι αντιμετώπισης που πρότεινα πιο πριν (να κάνουμε τις μεταβλητές από τρεις, δύο / να θέσουμε κατάλληλες μεταβλητές για να 'φύγει' η συνθήκη) μάλλον πιο πολύ δυσκολεύουν τα πράγματα παρά διευκολύνουν.
Ο πρώτος τρόπος θέλει αρκετό πραξολόι, ενώ για το δεύτερο διαβλέπω μια χρήση της ανισότητας της αναδιάταξης αλλά δεν έκατσα κάτω να το δω, οπότε δεν το 'χω και σίγουρο.
Και κάποιες γενικεύσεις πάνω στην ανισότητα (για ν - όρους υψωμένους στο τετράγωνο και στην k-οστή δύναμη), για όποιους ενδιαφερόμενους.
Ανκαι
,
τότε
1)
2)
3)
Οι αποδείξεις είναι εντελώς όμοιες με την αρχική (γίνεται και χρήση της γενικευμένης Andreescu)
Μια πιο δύσκολη άσκηση, πάνω σε αυτό το θέμα, είναι η εξής.
"Ανκαι
,
ν.δ.ο.
."
(νομίζω ότι ήταν και η τελευταία-τελευταία άσκηση σε κάποιο από τα βιβλία ανισοτήτων του Στεργίου)
Προτείνω, αν κάποιος θέλει να 'μπει' πιο πολύ στην ιδέα των ανισοτήτων δυσκολότερου επιπέδου, να ασχοληθεί με τις παρακάτω ασκήσεις για αρχή. (είναι και ξεκάθαρα μέσα στα πλαίσια της Α' Λυκείου)
1.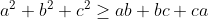
2.
(ενν. α,β,γ πραγματικοί)
Όσοι θέλουν κάτι πιο δύσκολο, έχω δύο ωραίες (και απλές για τους έμπειρους) ανισότητες προς απόδειξη.
1. Αν, τότε
(θυμίζει κάτι από την ανισότητα του δρ. τάσου)
2. Αν α,β μη-μηδενικοί πραγματικοί αριθμοί, τότε
Νομίζω ότι και οι δύο ανισότητες είχαν τεθεί παλιότερα σε κάτι βαλκανικούς, πχ. JBMO.
Η ΠΡωτη
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
wfgl
Νεοφερμένο μέλος


Έστω
Επίσης είναι :
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
wfgl
Νεοφερμένο μέλος


Δίνω κι εγώ μια με τη σειρά μου : Αν για τους αριθμούςκαι
ισχύει :
(1) Να λύσετε τις ανισώσεις :
α)
β)\chi +\frac{{\beta }^{10}+3{\beta }^{9}\chi }{2}>-\frac{\chi +2}{\beta -\alpha })
Να συγκριθούν οι αριθμοί :
Εχω και αλλες ωραιες αλλα δεν εχω καλο ιντερνετ μια κοβεται μια ερχεται μου εχει σπασει τα νευρα τελος παντων λυστε αυτη και βλεπουμε
--
και μια αλλη
Αν οι αριθμοίείναι θετικοί και :
,
να αποδειχθεί ότι.
Για την πρώτη άσκηση έχουμε
Με αντικατάσταση στο πρώτο ερώτημα προκύπτει
To δεύτερο ερώτημα με αντικατάσταση αποκτά την μορφή
Όσον αφορά την δεύτερη ισχύει ότι
Απόδειξη : (Θα χρησιμοποιήσω την μαθηματική επαγωγή ή μέθοδο της τέλειας επαγωγής)
Για να αποδείξουμε έναν μαθηματικό ισχυρισμό
α) Αποδεικνύουμε ότι η πρόταση
β)Υποθέτουμε ότι η πρόταση αληθεύει για το φυσικό κ=ν
γ)τέλος αποδεικνύουμε ότι η πρόταση ισχύει για ν=κ+1
για
Έστω ότι η πρόταση ισχύει για
Για
Θέτω
Άρα λόγω αυτής της ανισότητας έχουμε :
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 1 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 31 μέλη διάβασαν αυτό το θέμα:
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki


