qwerty111
Πολύ δραστήριο μέλος


Θεωρείται λάθος αν σπάσω ένα όριο σε άλλα επιμέρους κατευθείαν έχοντας υπολογίσει πρώτα με το μυαλό μου όμως ότι υπάρχουν; Πρέπει υποχρεωτικά να φαίνεται αυτή η σκέψη στην κόλλα;Ωπ, φάουλ. Μπορεί και να είσαι σωστός, αλλά δεν σπάμε ΠΟΤΕ όρια εάν δεν έχουμε πρώτα βεβαιωθεί ότι υπάρχουν και είναι πραγματικά!
Που σημαίνει ότι είναι "λάθος" να γράψεις εξ' αρχής:
Θα πρέπει πρώτα να γράψεις ότι:
, λόγω συνέχειας
Και μετά λες ότι επειδή τα επιμέρους όρια υπάρχουν και είναι πραγματικά τότε λες και ότι:
=\frac{1}{2}\lim_{x\rightarrow 0}x\cdot\lim_{x\rightarrow 0}x\ln{x}=\frac{1}{2}\cdot 0 \cdot f(0)=0)
Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Γιώργος
Τιμώμενο Μέλος


Ε, αυτά που θα κάνεις "με το μυαλό σου" γράψτα κι όλας. Δεν βλάπτει.Θεωρείται λάθος αν σπάσω ένα όριο σε άλλα επιμέρους κατευθείαν έχοντας υπολογίσει πρώτα με το μυαλό μου όμως ότι υπάρχουν; Πρέπει υποχρεωτικά να φαίνεται αυτή η σκέψη στην κόλλα;
Κατά τα άλλα, όλα είναι στην κρίση του διορθωτή. Εάν πρώτα δείξεις ότι υπάρχουν και είναι πραγματικά και μετά τα σπάσεις, είσαι καλυμμένος 100%. Από 'κει και πέρα ... ρισκάρεις.
Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
babisgr
Πολύ δραστήριο μέλος


και κάτι ακόμα:
έχουμε δυο μιγαδικούς z,w και ισχύουν: η εικόνα του z ανήκει στην (ε):
Αν ισχύει :
Μπορώ να πάρω τη σχέση
Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
vassilis498
Διακεκριμένο μέλος


Για το δεύτερο.
Καταρχάς ξέρεις ήδη ότι |z|=1
επίσης ότι
στην ουσία σου λέει ότι για τους μιγαδικούς w για τους οποίους ισχύει ότι |z-w|=1, να αποδείξεις ότι ισχύει |w|=2
ξεκινάς από το πρώτο, και εκμεταλλευόμενος τις σχέσεις που έχεις πας στο δεύτερο. Δοκίμασε να τετραγωνίσεις.
ΥΓ: δεν ξέρω αν βγαίνει κάτι αν κάνεις αυτό που λες, δεν το δοκίμασα, αλλά γενικά ναι, σε μια σχέση μπορείς να βάλεις μέτρα. Πρόσεξε όμως, μπορείς μόνο να βάλεις, όχι να βγάλεις.
Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
babisgr
Πολύ δραστήριο μέλος


Το πρώτο είναι σωστό, εφόσον σου λέει ότι το πεδίο ορισμού της f ( δηλαδή το σύνολο τιμών της αντίστροφης) είναι το R, τότε εκτός των άλλων η αντίστροφη θα παίρνει και την τιμή 0.
Σόρρυ, ήθελα να γράψω για τη παράγωγο της αντιστρόφου...

δηλαδή αυτό:
Αν
Αυτό τί είναι;
Ευχαριστώ!
Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
babisgr
Πολύ δραστήριο μέλος



Αλλά δεν έχουν και καμιά λογική τα δεδομένα με το ζητούμενο.. εκτός απο τη παραγωγιμότητα
Ευχαριστώ!
Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
babisgr
Πολύ δραστήριο μέλος


Β) Δίνεται
α) η F συνεχής στο [1,συν απειρο)
β) Αν F(e)=f(1) και ln(f(e))=1 νδο f(1)=1
Το πρώτο και το τελευταίο ερώτημα δε το έλυσα (τα bold)
Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
tebelis13
Πολύ δραστήριο μέλος


Α)Δίνεταινδο η g(x)=0 έχει μοναδική ρίζα στο [1,e].
Β) Δίνεται
και f'(x)>0 , f(0)=0 και
νδο:
α) η F συνεχής στο [1,συν απειρο)
β) Αν F(e)=f(1) και ln(f(e))=1 νδο f(1)=1
Το πρώτο και το τελευταίο ερώτημα δε το έλυσα (τα bold)
A)
στο [1,e] -> g γν. αύξουσα άρα με bolzano σε αυτό το διάστημα το ξ (όπως θές πέστο
 ) μοναδικό
) μοναδικό Σόρρυ για την συντομία αλλά βλέπω και champions

Aν δεν καταλαβαίνεις κάτι πές μου.
Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
babisgr
Πολύ δραστήριο μέλος



f:[0,3]->R παρ/μη με f' γν.μονότονη στο π.ο. της.
α) αν είναι f(1)+f(2)<f(0)+f(3) νδο η f είναι κυρτή στο [0,3] (το έδειξα)
β) αν είναι f'(0)=0 , f'(2)=4 και η εφαπτομένη στο Α(2,f(2)) τέμνει την εφαπτομένη στο Γ(0,f(0)) στο σημείο B(1,f(0)) νδο f(2)-f(0)=4 και ότι f(1)>f(0) (το έδειξα)
γ) αν
Δε μπορώ να δείξω το (γ)
Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Επειδή η f είναι κυρτή στο [0,1] η εφαπτομένη στο Γ θα βρίσκεται κάτω από την γραφική παράσταση της f για κάθε
Όμοια η f είναι κυρτή στο [1,2] οπότε για την εφαπτομένη στο Β θα ισχύει
To εμβαδόν του χωρίου (ΓΒΑ) επομένως θα είναι
Y.Γ. Το σχήμα είναι προσεγγιστικό

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
13diagoras
Δραστήριο μέλος


Οχι ,ετσι?
Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
vassilis498
Διακεκριμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
babisgr
Πολύ δραστήριο μέλος


Έστω
a)νδο για x>0 είναι
b) η F είναι γν. αύξουσα
Για το (α) λέω :
Επιπλέον για χ>0 είναι
Αλλιώς πως να το δείξω; (κάτι με το ότι είναι κοίλη θα βγαίνει αλλά δε το βρίσκω..)
2)Να βρεθεί ο x θετικός ακέραιος αν ισχύει: [(1-i) / i ]^x = 16
κάνοντας πράξεις προκύπτει: [ - (1+i) ] ^ x =16, μετά τί κάνω;
Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
tebelis13
Πολύ δραστήριο μέλος


Πρέπει ουσιαστικά ν.δ.ο1)Έστω f παραγωγίσιμη στο [0,+απειρο), f ' γν. φθινουσα στο π.ο. , f ' (0)=0 και f(x)>0
Έστω
a)νδο για x>0 είναι
b) η F είναι γν. αύξουσα
Για το (α) λέω :άρα η ζητούμενη σχέση γίνεται F(x)<0.
Επιπλέον για χ>0 είναι
Αλλιώς πως να το δείξω; (κάτι με το ότι είναι κοίλη θα βγαίνει αλλά δε το βρίσκω..)
2)Να βρεθεί ο x θετικός ακέραιος αν ισχύει: [(1-i) / i ]^x = 16
κάνοντας πράξεις προκύπτει: [ - (1+i) ] ^ x =16, μετά τί κάνω;
έστω
β)έστω
Αυτό πολύ ωραίο ερωτηματάκι!
Υ.Γ.Μπάμπη ωραίες ασκήσεις σου δίνει ο καθηγητής σου.

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
babisgr
Πολύ δραστήριο μέλος


Πρέπει ουσιαστικά ν.δ.ο
έστω
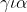
αρα

<h(0) \Rightarrow h(x)<0)

β)έστωκαι θα καταλήξεις στην αρχική που ισχύει
Αυτό πολύ ωραίο ερωτηματάκι!
Υ.Γ.Μπάμπη ωραίες ασκήσεις σου δίνει ο καθηγητής σου.
Ωραίες δίνει, αλλά και πάρα πολλές !!
 10 το minimum με προθεσμία 2-3 μέρες..
10 το minimum με προθεσμία 2-3 μέρες..Ευχαριστώ για τη βοήθεια!
Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Dmitsos
Πολύ δραστήριο μέλος


1)Έστω f παραγωγίσιμη στο [0,+απειρο), f ' γν. φθινουσα στο π.ο. , f ' (0)=0 και f(x)>0
Έστω
a)νδο για x>0 είναι
b) η F είναι γν. αύξουσα
Πρώτο post εδώ σαν νέο μέλος (Παρ' όλο που έχω γεράσει εδώ στο ischool, o Djimmakos είμαι :p)
Να δώσω μια λύση για το α ερώτημα γιατί εμείς σα μαθητές και σαν το μέλλον της Ελλάδα συχνά παρακινούμαστε να χρησιμοποιούμε το μυαλό μας και να ξεφεύγουμε από τη μεθοδολογία. Πάμε;
Θεωρώ τη συνάρτηση
Η f είναι παραγωγίσιμη στο [0,χ], άρα η G είναι συνεχής στο [0,χ] και παραγωγίσιμη στο (0,χ) με
Από το Θεώρημα Μέσης Τιμής υπάρχει ξ στο (0,χ) (το χ τυχαία επιλογή είπαμε, ε
 τέτοιο ώστε
τέτοιο ώστεΙσχύει (η f είναι γνησίως φθίνουσα)
(Eίναι όλα θετικά, γι' αυτό όταν αντιστρέφουμε αλλάζει η φορά)
Τώρα θα μου πείτε ότι δεν υπάρχει πιο καθοδηγούμενη μεθοδολογία απ' αυτό, αλλά τουλάχιστον ένα άσχετο ΘΜΤ πάντα "γοητεύει"
Για το δεύτερο απλώς παραγωγίζουμε.
Καλή μας επιτυχία!!
Nα βάλω και μια δεύτερη λύση για τους μιγαδικούς, παρ' όλο που μου άρεσε αυτή με το μέτρο που είδα πιο πάνω.
Για κάθε περιττό χ θα περισσεύει ένα i, οπότε δε μας κάνει, ευχαριστούμε.
Για χ=0,1,2, δε μας κάνει τίποτα.
Αρα το χ ειναι αρτιος μεγαλύτερος του 2.
Οπότε το i^x θα μας κάνει 1.
Οπότε 2^χ=256 => χ=8. Κάνουμε και μια επαλήθευση και είμαστε just!!
Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
babisgr
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
odoiporos
Νεοφερμένο μέλος


Αρχικά καλώς σας βρήκα! Γράφτηκα στο forum για να απαντήσω εδώ.1)Έστω f παραγωγίσιμη στο [0,+απειρο), f ' γν. φθινουσα στο π.ο. , f ' (0)=0 και f(x)>0
Έστω
a)νδο για x>0 είναι
b) η F είναι γν. αύξουσα
Είναι καλό πριν ακολουθήσουμε τον τυφλοσούρτη και πριν κάνουμε αλγεβρικές πράξεις, να έχουμε μία εικόνα του τι χειριζόμαστε...
Στην προκειμένη η εκφώνηση μιλάει για μία συνάρτηση στο [0,+οο) που είναι κοίλη (αφού f' γν. φθίνουσα) και γν. φθίνουσα (αφού f'(x) < f'(0)=0 για κάθε χ > 0). Φανταστείτε πώς μπορεί να "μοιάζει" μία τέτοια συνάρτηση. Φτιάξτε ένα γράφημά της (don't skip this step)... Ωραία. Τώρα η εκφώνηση συνεχίζει και λέει ότι η f(x)>0. Προσπαθήσετε να ενσωματώσετε και αυτόν τον περιορισμό στο γράφημά σας. Something is wrong? Yeap! Θα διαπιστώσετε ότι τέτοια συνάρτηση f δεν υπάρχει!!
Γιατί; Ας το δούμε λίγο πιο αυστηρά.
Έστω ότι υπάρχει. Τότε f(1) > 0 (αφού f(x) > 0) και f'(1) < 0.
Φέρτε την εφαπτομένη της γραφικής παράστασης στο σημείο (1,f(1)). Η εφαπτομένη θα έχει αρνητική κλίση, άρα θα τέμνει τον άξονα xx' για κάποιο
Εναλλακτικά, χωρίς χρήση του σχολίου: Υπολογίζουμε το
Καλή συνέχεια και καλή επιτυχία σε όλους σας!!
Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 2 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 232 μέλη διάβασαν αυτό το θέμα:
- Hased Babis
- ChrisG152
- giorgos5002
- Kougami
- giannis06
- Panagiwths12
- mikke
- hristosdab
- trifasikodiavasma
- haji
- thepigod762
- Mariosm.
- soulatso
- oteletampis
- phleidhs
- AggelikiGr
- sir ImPeCaBlE
- veiNqh
- Scandal
- alekos
- Debugging_Daemon
- just some guy
- xristosgkm
- ismember
- Apocalypse
- arrow25
- rempelos42
- ggl
- GStef
- QWERTY23
- xrisamikol
- Σωτηρία
- nikoletaz57
- _Aggelos123
- Mariam38
- SlimShady
- strsismos88
- Georgekk
- Lia 2006
- igeorgeoikonomo
- marian
- tsiobieman
- constansn
- Xristosdimitra
- Panagiotis849
- ρενακι 13
- Memetchi
- eukleidhs1821
- Nikkkpat
- Unboxholics
- korlef
- kwstaseL
- Thanos_D
- the purge
- T C
- Giii
- Papachrist
- liaiscool
- Αννα Τσιτα
- globglogabgalab
- Pharmacist01
- otinanai123
- abcdefg12345
- nicole1982
- thecrazycretan
- Ουριήλ
- kvstas92
- KingOfPop
- maria301
- Poirot
- papa2g
- stefan
- Κλημεντίνη
- TonyMontanaEse
- Lathy
- Alexecon1991
- Μάρκος Βασίλης
- Cortes
- το κοριτσι του μαη
- calliope
- ale
- panagiotis G
- Kleanth
- aggelosst9
- BioChemical
- spring day
- nucomer
- Georgia110
- LeoDel
- pink_panther
- Alexandros973
- marsenis
- den antexw allh apotyxia
- KaterinaL
- kiyoshi
- drosos
- Λαμπρινηη
- Bill22
- Chrysablac.
- giorgosp97
- Βλα
- Monster Hunter
- jul25
- xxxtolis
- Stroka
- nicks1999
- totiloz
- Earendil
- mitsakos
- tasost
- lnesb
- ssalex
- alan09
- Livaja10
- χημεια4λαιφ
- Viedo
- UncleJ
- Kostakis45
- Infrared
- Zgian
- pepatogourounaki
- hirasawayui
- GeoCommand
- Eleni54
- American Economist
- EiriniS20
- ΘανάσοςG4
- stamoul1s
- Αριάνα123
- uni77
- Libertus
- tasoss
- PanosCh002
- Unseen skygge
- Νικόλας Ραπ.
- cel123
- The Limit Does Not Exist
- don_vito
- suaimhneas
- Αλκης Κ.
- alexrami
- Baggelitsa36
- Νομικάριος13
- spinalgr1990
- d_th
- Adolfo valencia
- Πα.Κ
- Vasilis25
- Johnman97
- Steffie88
- rekcoR
- gwgw_5
- fockos
- Mariahj
- roud
- kostas83
- Cpt.Philips
- Makis45
- Χρησλου
- Panos_02
- Vold
- tymvorixos
- GiorgosAsi
- Neos167
- theodoraooo
- George187
- Άρτεμις Α.
- Μαρία2222
- christos87
- Idontknoww
- jimis2001
- Metamorph
- Γατόπαρδος.
- Johnsk
- mitsos14
- johnsiak
- Elel
- Dreamer_SW
- Γιαννης1987Θεσσ
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki



