Συλλογή ασκήσεων και τεστ στα Μαθηματικά Προσανατολισμού

tebelis13 · 27-03-11

Έστω συνεχής συναρτηση f με $f(x)\neq 0 \kappa \alpha \iota f(x)=2010+\int_{0}^{x}t/f(t)dt$
Να βρεθεί η μονοτονία της f καθώς και ο τύπος της
Ακόμα να βρεθεί η μονοτονία της $h(x)=f^2(x)/(x*2010)^2$
αλλά και το $\lim_{+\propto }\int_{x}^{x+1}h(t)dt$

g.l.

Έγραψα με λάτεξ :o

13diagoras · 27-03-11

Να δειξετε οτι αν α1,α2,...,αν >0 με α1.α2.α3 ...αν=1,τοτε α1+α2+α3+...+αν>=ν
(χωρις χρηση ταυτοτητας Cauchy)

Υποδειξη: Μελετηστε τη μονοτονια της e^x - ex

red span · 28-03-11

Αρχική Δημοσίευση από 13diagoras:
Να δειξετε οτι αν α1,α2,...,αν >0 με α1.α2.α3 ...αν=1,τοτε α1+α2+α3+...+αν>=ν
(χωρις χρηση ταυτοτητας Cauchy)

Υποδειξη: Μελετηστε τη μονοτονια της e^x - ex

Να την επεκτινω
Αν Ισχυει αυτο που λεει ο διαγορας να δειξετε οτι α1*α2*α3*α4............αν=1

13diagoras · 28 Μαρτίου 2011

Ρε,ξαναδιαβασε τι λεει

Αυτο ειναι το δεδομενο!

Υ.Γ.Πως και δεν σου φανηκε "κουκου" η ασκηση?? :hmm:

red span · 29-03-11

Αν ισχυει α1+α2+α3+...+αν>=ν τοτε δειξτε α1*α2*α3*α4............αν=1
Ας δουμε και το αντιστροφο Δοκιμαστε το θεωρημα Φερμα

math21 · 30-03-11

Bρήκα Θέματα Προσομοίωσης
https://tsekuras-frontistiria.blogspot.com/p/blog-page_11.html

red span · 31-03-11

Αρχική Δημοσίευση από red span:
Αν ισχυει α1+α2+α3+...+αν>=ν τοτε δειξτε α1*α2*α3*α4............αν=1
Ας δουμε και το αντιστροφο Δοκιμαστε το θεωρημα Φερμα

Δεν θελω να χαθει
Αποτελει μερος της γενισκευσης Αν α1,α2,α3 θετικοι διαφοροι του 1 και κ1,κ2,κ3 πραγματικοι τοτε για καθε τιμη του πραγματικου χ ισχυει κ1*α1+κ2*α2+............κν*αν>=κ1+κ2+.........κν τοτε αποδειξτε οτι α^κ1*α^κ2+.........αν^κν=1
βγαινει ευκολα με το θ.φερμα θετεις συναρτηση και ευκολα καταληγεις συναρτηση.
Ας την αφησουμε αυτη λεω να αρχισουμε να βαζουμε ασκησεις στο κλιμα των πανελληνιων,στην ιδια κλιμακα δυσκολιας
Τι λετε βασιλη,διαγορα και οι αλλοι?

tebelis13 · 31-03-11

Αρχική Δημοσίευση από red span:
Ας την αφησουμε αυτη λεω να αρχισουμε να βαζουμε ασκησεις στο κλιμα των πανελληνιων,στην ιδια κλιμακα δυσκολιας
Τι λετε βασιλη,διαγορα και οι αλλοι?

Αρχική Δημοσίευση από tebelis13:
Έστω συνεχής συναρτηση f με $f(x)\neq 0 \kappa \alpha \iota f(x)=2010+\int_{0}^{x}t/f(t)dt$
Να βρεθεί η μονοτονία της f καθώς και ο τύπος της
Ακόμα να βρεθεί η μονοτονία της $h(x)=f^2(x)/(x*2010)^2$
αλλά και το $\lim_{+\propto }\int_{x}^{x+1}h(t)dt$

^

vassilis498 · 31-03-11

Αρχική Δημοσίευση από tebelis13:
Έστω συνεχής συναρτηση f με $f(x)\neq 0 \kappa \alpha \iota f(x)=2010+\int_{0}^{x}t/f(t)dt$
Να βρεθεί η μονοτονία της f καθώς και ο τύπος της
Ακόμα να βρεθεί η μονοτονία της $h(x)=f^2(x)/(x*2010)^2$
αλλά και το $\lim_{+\propto }\int_{x}^{x+1}h(t)dt$

g.l.

Έγραψα με λάτεξ :o

$f(x)=2010+\int_{0}^{x}\frac{t}{f(t)}dt,(1)$

f(0)=2010

παραγωγίζω
$f'(x)=\frac{x}{f(x)}, f'(0)=0$

$f'(x)=\frac{x}{f(x)}\Leftrightarrow f'(x)f(x)=x\Leftrightarrow 2f'(x)f(x)=2x$

${f}^{2}(x)={x}^{2}+c$

για x=0 παίρνω c=2010², άρα ${f}^{2}(x)={x}^{2}+{2010}^{2}\Leftrightarrow f(x)=\sqrt{{x}^{2}+{2010}^{2}},x\epsilon R$

$f'(x)\leq 0\Leftrightarrow \frac{x}{f(x)}\leq 0\Leftrightarrow x\leq 0$

άρα f γν. αύξουσα στα θετικά, και γν. φθίνουσα στα αρνητικά

$h(x)=\frac{{f}^{2}(x)}{{x}^{2}{2010}^{2}}=\frac{{x}^{2}+{2010}^{2}}{{x}^{2}{2010}^{2}}=\frac{1}{{2010}^{2}}+\frac{1}{{x}^{2}}$

$h'(x)=-\frac{2}{{x}^{3}}$

$h'(x)\leq 0\Leftrightarrow -\frac{2}{{x}^{3}}\leq 0\Leftrightarrow x\geq 0$

άρα h(x) γν. αύξουσα στα αρνητικά, και γν. φθίνουσα στα θετικά.

$\int_{x}^{x+1}h(t)dt=\int_{x}^{x+1}\frac{1}{{2010}^{2}}+\frac{1}{{t}^{2}}dt=\left[\frac{t}{{2010}^{2}}-\frac{1}{t} \right]=\frac{x+1}{{2010}^{2}}-\frac{1}{x+1}-\frac{x}{{2010}^{2}}+\frac{1}{x}=\frac{1}{{2010}^{2}}+\frac{1}{x}-\frac{1}{x+1}$

$\lim_{x\rightarrow +\propto }\int_{x}^{x+1}h(t)dt=\lim_{x\rightarrow +\propto }\left[\frac{1}{{2010}^{2}}+\frac{1}{x}-\frac{1}{x+1} \right]=\frac{1}{{2010}^{2}}$

13diagoras · 31-03-11

Αρχική Δημοσίευση από red span:
Τι λετε βασιλη,διαγορα και οι αλλοι?

Ωραιος!!Παμε να φτασουμε στα 5000 ποστ

(Λειπει το +οο)

red span · 05-04-11

Μια ασκηση επιπεδου 4 Θεματος
Εστω συναρτηση f συνεχης τετοια ωστε για καθε χ ε R να ισχυει
f(x)+e^f(x)=x+x*(e^x)
ΝΑ δειξετε οτι
a) Αν α<>β τοτε f(α)<>f(β)
Β)Αν α+f(a)=β +f(β) τοτε α=β
γ)Υπαρχει χο ε R ωστε φ(χο)=0
δ)Υπαρχει ξ ε R τετοιος ωστε f(ξ)=ξ
ε)f(R)=R
Επισης θελω να πω αν θελετε να δειτε τα θεματα των επαναληπτικων του 2010 παρουσιαζουν ιδιαιτερο ενδιαφερον

13diagoras · 05-04-11

Τα (α),(β), βγαινουν.
Στο (γ) αποδεικνυεις οτι φ(0)<0 και φ(1)>0
Στο (δ) κατι δεν μου αρεσει εκτος αν εκανα κατι λαθος.Απεδειξα οτι φ(1)=1. :hmm:

Υ.Γ.Δεν σας αρεσε αυτη που εβαλα?.Ας ασχοληθει καποιος να βαλουμε και τη λυση

red span · 05-04-11

Αρχική Δημοσίευση από 13diagoras:
Τα (α),(β), βγαινουν.
Στο (γ) αποδεικνυεις οτι φ(0)<0 και φ(1)>0
Στο (δ) κατι δεν μου αρεσει εκτος αν εκανα κατι λαθος.Απεδειξα οτι φ(1)=1.

Υ.Γ.Δεν σας αρεσε αυτη που εβαλα?.Ας ασχοληθει καποιος να βαλουμε και τη λυση

Tωρα εσυ το λες αυτο λυση???? :/:

13diagoras · 05-04-11

Αρχική Δημοσίευση από red span:
Tωρα εσυ το λες αυτο λυση????

Δεν το λεω λυση,δεν ηταν και ο σκοπος μου αυτος.
Ηθελα απλως να δω αν το ειχα σωστο γιατι κατι δεν μου αρεσε(οπως ειπα)στο δ ερωτημα,ωστε σε δευτερη φαση να παραθεσω την λυση. :/:

vassilis498 · 06-04-11

Αρχική Δημοσίευση από red span:
Μια ασκηση επιπεδου 4 Θεματος
Εστω συναρτηση f συνεχης τετοια ωστε για καθε χ ε R να ισχυει
f(x)+e^f(x)=x+x*(e^x)
ΝΑ δειξετε οτι
a) Αν α<>β τοτε f(α)<>f(β)
Β)Αν α+f(a)=β +f(β) τοτε α=β
γ)Υπαρχει χο ε R ωστε φ(χο)=0
δ)Υπαρχει ξ ε R τετοιος ωστε f(ξ)=ξ
ε)f(R)=R
Επισης θελω να πω αν θελετε να δειτε τα θεματα των επαναληπτικων του 2010 παρουσιαζουν ιδιαιτερο ενδιαφερον

βάζω κι εγώ μια προσπαθεια

$f(x)+{e}^{f(x)}=x+x{e}^{x}$

έστω οι συναρτήσεις

$h(x)=x+{e}^{x}$

$g(x)=x+x{e}^{x}$

$p(x)=g(x)-h(x)={e}^{x}(x-1)$

$q(x)=f(x)+x$

όλες ορισμένες στο R.

$h'(x)={e}^{x}+1>0$ , άρα h(x) γν αύξουσα

$g'(x)=x{e}^{x}+{e}^{x}+1$ και $g''(x)={e}^{x}(x+2)$

από πινακάκι στο R βλέπω ότι η g' έχει ελάχιστο στο x=-2, στο οποίο είναι θετική. g'(x)>0, άρα g(x) γν. αύξουσα

από όρια στο -οο και το +οο βλέπω ότι h και g έχουν σύνολο τιμών το R.

$p'(x)=x{e}^{x}$ , από πινακάκι στο R βλέπω ότι έχει ελάχιστο στο x=0 στο οποίο κάνει -1.

επίσης $\lim_{x\rightarrow +\propto }p(x)=+\propto$ , άρα το σύνολο τιμών της p(x) είναι το [-1, +οο).

τώρα

α) με βάση τις συναρτήσεις που έχω θέσει η σχέση που μου δίνεται γίνεται

$h(f(x))=g(x)$

για x1,x2 στο R τέτοια ώστε x1<x2

$x1<x2\Leftrightarrow g(x1)<g(x2)\Leftrightarrow h(f(x1))<h(f(x2))\Leftrightarrow f(x1)<f(x2)$ άρα f γν αύξουσα και "1-1".

συνεπώς για $\alpha \neq \beta \Leftrightarrow f(\alpha )\neq f(\beta )$

β) ξέρω ότι f γν. αύξουσα άρα από ορισμό ( 2 σχέσεις και προσθέτω κατά μέλη) q(x) γν αύξουσα άρα και "1-1"

$\alpha +f(\alpha )=\beta +f(\beta )\Leftrightarrow q(\alpha )=q(\beta )\Leftrightarrow \alpha =\beta$

γ) στην σχέση που δίνεται αντικαθιστώ x=0 και έχω

$f(0)+{e}^{f(0)}=0\Leftrightarrow f(0)=-{e}^{f(0)}<0$

έστω ότι f(x)<0 για κάθε x στο R.

$f(x)<0\Leftrightarrow h(f(x))<h(0)\Leftrightarrow g(x)<1$ άτοπο γιατί έχει σύνολο τιμών το R , άρα έχω x1 τέτοιο ώστε f(x1)>0
f συνεχής, από Bolzano, έχω Xo ανάμεσα σε αυτό και το 0 τέτοιο ώστε f(Xo)=0

δ) έστω f(x)>x για κάθε x στο R.

$f(x)>x\Leftrightarrow h(f(x))>h(x)\Leftrightarrow g(x)>h(x)\Leftrightarrow g(x)-h(x)>0\Leftrightarrow p(x)>0$ , άτοπο γιατί η p(x) παίρνει και αρνητικές τιμές.
αντίστοιχα για f(x)<x
άρα έχω ένα τουλάχιστον x τέτοιο ώστε f(x)=x

ε) h(x) γν αύξουσα, "1-1" και αντιστρέψιμη

$h(f(x))=g(x)\Leftrightarrow f(x)={h}^{-1}(g(x))$
επίσης
για x1,x2 στο R τέτοια ώστε x1<x2

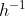
$x1<x2\Leftrightarrow h({h}^{-1}(x1)< h({h}^{-1}(x2)\Leftrightarrow {h}^{-1}(x1)<{h}^{-1}(x2)$ , άρα ${h}^{-1}$ γν. αύξουσα
επίσης αφού το πεδίο ορισμού της h είναι το R, και το σύνολο τιμών της αντίστροφης είναι το R.

άρα $\lim_{x\rightarrow -oo}{h}^{-1}(x)=-\propto$ και $\lim_{x\rightarrow +\propto }{h}^{-1}(x)=+\propto$

$\lim_{x\rightarrow -\propto }f(x)=\lim_{x\rightarrow -\propto }{h}^{-1}(g(x))$ θέτω u=g(x) $\lim_{x\rightarrow -\propto }g(x)=-\propto$

άρα το όριο γίνεται $\lim_{u\rightarrow -\propto }{h}^{-1}(u)=-\propto$
αντίστοιχα και το άλλο όριο.
Επίσης f γν. αύξουσα άρα το σύνολο τιμών της είναι το R.

red span · 06-04-11

Αρχική Δημοσίευση από 13diagoras:
Τα (α),(β), βγαινουν.
Στο (γ) αποδεικνυεις οτι φ(0)<0 και φ(1)>0
Στο (δ) κατι δεν μου αρεσει εκτος αν εκανα κατι λαθος.Απεδειξα οτι φ(1)=1.

Υ.Γ.Δεν σας αρεσε αυτη που εβαλα?.Ας ασχοληθει καποιος να βαλουμε και τη λυση

Στο δ μια χαρα το βρικες.Απλα να ξες οτι θελει οποσδηποτε να το επαληθευσεις στην αρχικη την σχεση

Metal-Militiaman · 06-04-11

Αρχική Δημοσίευση από 13diagoras:
Ωραιος!!Παμε να φτασουμε στα 5000 ποστ

(Λειπει το +οο)

i) $\; \; \; h'(x)={e}^{-x}f'(x)-{e}^{-x}f(x)={e}^{-x}(f'(x)-f(x))$
$f''(x)-f'(x)>0\Rightarrow (f'(x)-f(x))'>0$ άρα $f'(x)-f(x)$ γν. αύξουσα στο $[0,+\propto)$
(μπορούμε και να ολοκληρώσουμε στο [0,χ] χ>0 την ανισότητα f''(t)>f'(t) και θα καταλήξουμε στη σχέση f'(x)>f(x),χ>0)

$x>0\Rightarrow f'(x)>f(x)$
$h'(x)>0$ για $x>0$ οπότε $h(x)$ γν. αύξουσα στο $[0,+\propto)$

ii) $\; \; \; {({f}^{2}(x))''=(2f(x)f'(x))'=2({f'}^{2}(x)+f(x)f''(x))$
$x>0\Rightarrow h(x)>0\Rightarrow {e}^{-x}f(x)>0\Rightarrow f(x)>0$
$f''(x)>f'(x)>f(x)>0 \; \; ,x>0$ (f γν. αύξουσα και κυρτή) (Σ)
$({f}^{2}(x))'' >0$ για $x>0$
${f}^{2}(x)$ κυρτή στο $[0,+\propto)$

iii) Έστω ${x}_{0}$ εσωτερικό σημείο του $[0,+\propto)$ και από τη σχέση (Σ) η f είναι κυρτή επομένως θα ισχύει
$f(x)\geq f({x}_{0})+f'({x}_{0})(x-{x}_{0})$

$\lim_{x\rightarrow +\propto }f({x}_{0})+f'({x}_{0})(x-{x}_{0})=+\propto$

$\lim_{x\rightarrow +\propto }f(x)=+\propto$

13diagoras · 6 Απριλίου 2011

Ωραιος!

Αρχική Δημοσίευση από red span:
Στο δ μια χαρα το βρικες.Απλα να ξες οτι θελει οποσδηποτε να το επαληθευσεις στην αρχικη την σχεση

Βασικα μιλαμε στα τυφλα.Επειδη βιαζομαι για μαθημα,το λεω απλα ελπιζοντας να μην σε απογοητευσω παλε...
εβαλα στην δοθησα οπου χ το 1 και θεωρησα την σχεση που προκυπτει(Εστω α).Αυτη ειναι γνησια αυξουσα και α(1)=α(φ(1)) αρα φ(1)=1.Οποτε δεν βρισκω καποιον λογο για να χρειαζεται επαληθευση,αφου οδηγηθηκαμε στο συμπερασμα με ισοδυναμιες.
Για πες την αποψη σου...

vassilis498 · 06-04-11

Αρχική Δημοσίευση από Metal-Militiaman:
i) $\; \; \; h'(x)={e}^{-x}f'(x)-{e}^{-x}f(x)={e}^{-x}(f'(x)-f(x))$
$f''(x)-f'(x)>0\Rightarrow (f'(x)-f(x))'>0$ άρα $f'(x)-f(x)$ γν. αύξουσα στο $[0,+\propto)$
(μπορούμε και να ολοκληρώσουμε στο [0,χ] χ>0 την ανισότητα f''(t)>f'(t) και θα καταλήξουμε στη σχέση f'(x)>f(x),χ>0)

$x>0\Rightarrow f'(x)>f(x)$
$h'(x)>0$ για $x>0$ οπότε $h(x)$ γν. αύξουσα στο $[0,+\propto)$

ii) $\; \; \; {({f}^{2}(x))''=(2f(x)f'(x))'=2({f'}^{2}(x)+f(x)f''(x))$
$x>0\Rightarrow h(x)>0\Rightarrow {e}^{-x}f(x)>0\Rightarrow f(x)>0$
$f''(x)>f'(x)>f(x)>0 \; \; ,x>0$ (f γν. αύξουσα και κυρτή) (Σ)
$({f}^{2}(x))'' >0$ για $x>0$
${f}^{2}(x)$ κυρτή στο $[0,+\propto)$

iii) Έστω ${x}_{0}$ εσωτερικό σημείο του $[0,+\propto)$ και από τη σχέση (Σ) η f είναι κυρτή επομένως θα ισχύει
$f(x)\geq f({x}_{0})+f'({x}_{0})(x-{x}_{0})$

$\lim_{x\rightarrow +\propto }f({x}_{0})+f'({x}_{0})(x-{x}_{0})=+\propto$

$\lim_{x\rightarrow +\propto }f(x)=+\propto$

ωραίο αυτό με την εφαπτομένη δεν το χα σκεφτεί

lowbaper92 · 07-04-11

Παίδες έχετε τελειώσει την ύλη? Να αρχίσω να ανεβάζω καμιά επαναληπτική?

Συλλογή ασκήσεων και τεστ στα Μαθηματικά Προσανατολισμού

Πολύ δραστήριο μέλος

Δραστήριο μέλος

Δραστήριο μέλος

Δραστήριο μέλος

Δραστήριο μέλος

Νεοφερμένος

Δραστήριο μέλος

Πολύ δραστήριο μέλος

Διακεκριμένο μέλος

Δραστήριο μέλος

Συνημμένα

Δραστήριο μέλος

Δραστήριο μέλος

Δραστήριο μέλος

Δραστήριο μέλος

Διακεκριμένο μέλος

Δραστήριο μέλος

Νεοφερμένος

Δραστήριο μέλος

Διακεκριμένο μέλος

Πολύ δραστήριο μέλος