mariza_93
Δραστήριο μέλος


Ορίστε μια ακόμα.
Να βρείτε που κινούνται οι εικόνες τον μιγαδικών z για τους οποίους ισχύει.
Μην την υποτιμήσετε έχει κάτι έξυπνο στο τέλος.
οριστε κ ο δευτερος τροπος......
ειναι η τελευταια φορα που γραφω με το latex .....μιση ωρα για μια ασκηση......


Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Dias
Επιφανές μέλος


Αν μια άσκηση δεν έχει κλάσματα και όρια δεν είναι απαραίτητο το lastex. Για τη λύση που έγραψες δεν χρειαζόταν. Το | και το ² βγαίνουν κατευθείαν από το πληκτρολόγιο και το z̅ το γράφεις στο word και το επικολλάς.ειναι η τελευταια φορα που γραφω με το latex .....μιση ωρα για μια ασκηση......


Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


Έστωσυνεχής με
. Να εξεταστεί αν η f είναι 1-1
Είναι f(4)=(f(1)f(2)f(3))^(1/3)
Για κάθε x στο [1,4] ισχύει f(x)>0.
Η f είναι συνεχής στο [1,3] γνήσιο υποσύνολο του [1,4], οπότε υπάρχουν πραγματικοί αριθμοί m, M με 0<m<Μ τέτοιοι ώστε να ισχύει m<=f(x)<=M για κάθε x στο διάστημα [1,3] (θεώρημα μέγιστης-ελάχιστης τιμής συνεχούς συνάρτησης). Επομένως έχουμε:
m<=f(1)<=M, m<=f(2)<=M και m<=f(3)<=M. Επειδή όλοι οι όροι των 3 ανισοτήτων είναι θετικοί, μπορεί να γίνει πολλαπλασιασμός κατά μέλη διατηρώντας τη φορά των ανισοτήτων, οπότε:
m³<=f(1)f(2)f(3)<=M³ => m<=(f(1)f(2)f(3))^(1/3)<=M
Συνεπώς σύμφωνα με το θεώρημα ενδιαμέσων τιμών συνεχών συναρτήσεων, υπάρχει ξ στο [1,3] τέτοιο ώστε f(ξ)=(f(1)f(2)f(3))^(1/3).
Επειδή ξ<4 => ξ διάφορο 4 και f(ξ)=f(4) τότε η f δεν είναι 1-1.
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Leo 93
Εκκολαπτόμενο μέλος


Έστωσυνεχής με
. Να εξεταστεί αν η f είναι 1-1
Άλλος τρόπος:
Η δοσμένη γράφεται
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Η συνάρτηση f είναι αύξουσα στο R, οπότε για κάθε x1, x2 στο R με x1<x2 ισχύει f(x1)<=f(x2).
Θεωρώ την συνάρτηση g(x)=f(x)+x. Η g είναι συνεχής στο R ως άθροισμα συνεχών στο R συναρτήσεων.
Για κάθε x1, x2 στο R με x1<x2 ισχύει f(x1)<=f(x2). Προσθέτοντας κατά μέλη τις 2 τελευταίες ανισότητες προκύπτει f(x1)+x1<f(x2)+x2 => g(x1)<g(x2).
Άρα για κάθε x1, x2 στο R με x1<x2 ισχύει g(x1)<g(x2). Επομένως η συνάρτηση g είναι γνησίως αύξουσα στο R και συνεπώς είναι 1-1.
Η f είναι συνεχής στο R. Συνεπώς σύμφωνα με το θεώρημα μέγιστης-ελάχιστης τιμής συνεχών συναρτήσεων, για κάθε x στο R υπάρχουν m, M στο R τέτοιοι ώστε m<=f(x)<=M για κάθε x στο R.
m<=f(x)<=M => m+x<=f(x)+x<=M+x => m+x<=g(x)<=M+x για κάθε x στο R.
lim(x->-άπειρο)(m+x)=lim(x->-άπειρο)(M+x)=-άπειρο
Σύμφωνα με το κριτήριο παρεμβολής είναι lim(x->-άπειρο)g(x)=-άπειρο.
Από τον ορισμό του ορίου προκύπτει ότι υπάρχει α<0 ώστε για κάθε x στο (-άπειρο, α) να υπάρχει m΄<0 τέτοιο ώστε g(x)<m΄ για κάθε x στο (-άπειρο, α). Επειδή g(x)<m΄ και m΄<0 τότε g(x)<0 για κάθε x στο (-άπειρο, α). Άρα υπάρχει χ1 στο (-άπειρο,α) τέτοιο ώστε g(x1)<0.
lim(x->+άπειρο)(m+x)=lim(x->+άπειρο)(M+x)=+άπειρο
Σύμφωνα με το κριτήριο παρεμβολής είναι lim(x->+άπειρο)g(x)=+άπειρο.
Από τον ορισμό του ορίου προκύπτει ότι υπάρχει β>0 ώστε για κάθε x στο (β, +άπειρο) να υπάρχει M΄>0 τέτοιο ώστε g(x)>M΄ για κάθε x στο (β, +άπειρο). Επειδή g(x)>M΄ και Μ΄>0 τότε g(x)>0 για κάθε x στο (β, +άπειρο). Άρα υπάρχει χ2 στο (β, +άπειρο) τέτοιο ώστε g(x2)>0.
Η συνάρτηση g είναι συνεχής στο [x1, x2] και ισχύει g(x1)g(x2)<0. Σύμφωνα με το θεώρημα Bolzano υπάρχει τουλάχιστον ένα x0 στο (x1, x2) τέτοιο ώστε g(x0)=0.
Επειδή η g είναι 1-1, τότε υπάρχει μοναδικό x0 τέτοιο ώστε g(x0)=0 => f(x0)=-x0
Γιώργο ξαναδές το λίγο. Για να πάρεις Θεώρημα Μέγιστης και Ελάχιστης Τιμής η f πρέπει να είναι ορισμένη σε κάποιο κλειστό διάστημα. Παραθέτω μια λύση που μου έδωσαν
Έστω
και
Άπο Θ.Bolzano υπάρχει τουλάχιστον ένα
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Αυτή μπαίνει με μία επιφύλαξη γιατί δεν ξέρω αν είναι εντός ύλης οι ν-οστές ρίζες της μονάδας!
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Leo 93
Εκκολαπτόμενο μέλος



Μία που τη βρήκα στο mathematica και μου άρεσε.
ΑΣΚΗΣΗ
Να υπολογιστεί το
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


Μία που τη βρήκα στο mathematica και μου άρεσε.
ΑΣΚΗΣΗ
Να υπολογιστεί το
χρειάζεται γνώσεις διαφορικού λογισμού
Από το κριτήριο παρεμβολής προκύπτει ότι το ζητούμενο όριο είναι ίσο με 0.
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
koum
Πολύ δραστήριο μέλος


Έστωτέτοιος ώστε
. Να δείξετε ότι
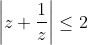
Έχουμε:
Οπότε:
Οπότε και
Από θέματα της ΕΜΕ είναι η άσκηση; Κάπου την έχω ξαναδεί...

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Έστω
και
Υπόδειξη: Προσπαθείστε να βρείτε ένα διάστημα όπου μπορεί να εφαρμοστεί το θεώρημα του Fermat
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
red span
Δραστήριο μέλος


μπορει παντως την εχουνε πολλα βοηθηματα οπως του στεργιουΈχουμε:
Οπότε:, η οποία είναι της μορφής
Οπότε και
Από θέματα της ΕΜΕ είναι η άσκηση; Κάπου την έχω ξαναδεί...
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
koum
Πολύ δραστήριο μέλος


Και μία λίγο διεστραμμένη:
Έστωδύο φορές παραγωγίσιμη, τέτοια ώστε
και. Δείξτε ότι υπάρχει
τέτοιο ώστε
Υπόδειξη: Προσπαθείστε να βρείτε ένα διάστημα όπου μπορεί να εφαρμοστεί το θεώρημα του Fermat
Δίνω απλά μια ιδέα, γιατί το να κάτσω να τη γράψω όλη είναι κομματάκι βαρύ.

Έστω:
Παρατηρούμε ότι
Οπότε αρκεί να δείξουμε ότι υπάρχει
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Cloud_Strife
Νεοφερμένο μέλος


Να υπολογίσετε το όριο:
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


Ένα από τα αγαπημένα μου όρια:
Να υπολογίσετε το όριο:
^{x}-e)
μηδέν
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Cloud_Strife
Νεοφερμένο μέλος


Πάντως ελάχιστοι είναι αυτοί που ξέρουν τον ορισμό του παραπάνω ορίου, πόσο μάλλον το σωστό υπολογισμό του (Μαθητές Λυκείου πάντα). Το αποτέλεσμα είναι μηδέν, αν και μια βιαστική επίλυση θα έδινε άπειρο και ούτε καν 1-e...μηδέν
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 1 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 289 μέλη διάβασαν αυτό το θέμα:
- Maynard
- foxypup
- Pars3c
- mikke
- thepigod762
- 98.8%chimpanzee
- trifasikodiavasma
- ggl
- ioanna2007
- Hased Babis
- Mariosm.
- infection54
- Jesse_
- topg
- eukleidhs1821
- bill09876
- Debugging_Demon
- mali
- Joji
- Ness
- Helen06
- Scandal
- synthnightingale
- arko
- BillyTheKid
- Magigi
- Paragontas7000
- Unboxholics
- just some guy
- george777
- Wonderkid
- Micro
- IceCream05
- Abiogenesis
- GeorgePap2003
- katia.m
- giannhs2001
- paul
- Praxis
- Apocalypse
- shezza94
- desp1naa
- rempelos42
- Sherlockina
- oups
- Dimgeb
- spring day
- KingOfPop
- mpapa
- Chrisa
- Physicsstudent
- tsiobieman
- P.Dam.
- persi
- theodoraooo
- PanosBat
- kost28
- mikriarchitectonissa
- BILL KEXA
- Dr. Gl. Luminous
- Eleftheria2
- Lathy
- bruh_234
- Miranda32
- SlimShady
- kallikd
- nucomer
- alpha.kappa
- Eeeee
- J.Cameron
- Marple
- Kitana
- F1L1PAS
- sophiaa
- VFD59
- papa2g
- το κοριτσι του μαη
- srg96
- Hopeful22
- Φινεύς
- Phys39
- Anta2004
- fairyelly
- Pharmacist01
- jYanniss
- Panagiotis849
- Kokro
- augustine
- Nikoletaant
- Mashiro@Iberan
- margik
- Mammy Nun
- Pastramis
- Σωτηρία
- Appolon
- panosveki
- Nickt23
- igeorgeoikonomo
- Steliosgkougkou
- QWERTY23
- Ameliak
- aladdin
- nimbus
- Φωτεινη Τζα.
- marian
- Georgekk
- xrisamikol
- Poirot
- the purge
- Dora140303
- Machris
- s93060
- Nikitas18
- Stif6
- stav.mdp
- damn
- aekaras 21
- Anthropaki
- Angelos12345
- ioannam
- Μάρκος Βασίλης
- skyway
- Nick2325
- Nala
- Manolo165
- Ryuzaki
- T C
- Devilshjoker
- El_
- George9989
- TonyMontanaEse
- globglogabgalab
- constansn
- barkos
- katerinavld
- fenia
- An_uknown_world
- Jimmis18
- maria2001
- KingPoul
- Xara
- thecrazycretan
- abcdefg12345
- Κλημεντίνη
- ale
- panagiotis G
- mechaniceng
- Giii
- calliope
- Tequila
- natalix
- Ουριήλ
- Cortes
- Alexecon1991
- pepsoula
- Mariaathens
- Lia 2006
- 1205
- παιδι για κλαματα
- Alexandros36k
- alexd99
- chembam
- Specon
- Dr House
- panagiotis23
- Johnman97
- rhymeasylum
- Αννα Τσιτα
- KaterinaL
- Libertus
- LeoDel
- iminspain
- den antexw allh apotyxia
- Λαμπρινηη
- Mendel2003
- Ijt
- drosos
- Κορώνα
- JohnGreek
- Αρχηγος_β3
- alexandra_
- ΘανάσοςG4
- Dimitris9
- Birtjan
- george7cr7
- NickT
- Bgpanos
- JKTHEMAN
- nicole1982
- χημεια4λαιφ
- Stroka
- Kostakis45
- charmander
- leo41
- EiriniS20
- Αριάνα123
- MarilynSt
- iManosX13
- Nefh_
- Viedo
- Βλα
- suaimhneas
- george pol
- kristinbacktoschool
- fearless
- Rene2004
- Steffie88
- Slytherin
- jimnikol21
- Unseen skygge
- cel123
- jul25
- Thanos_D
- Ireneeneri
- tasost
- Mukumbura
- xxxtolis
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki



