koum
Πολύ δραστήριο μέλος


1)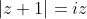
2)
3)
4) Aννα βρείτε
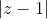
Είναι ασκήσεις που παρόμοιές τους έχουν λυθεί στο ίδιο topic. Κάνε μια προσπάθεια. Δεν είναι δύσκολες.
Κάνε κάτι με το latex please...

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


Εγώ δεν έχω χρόνο να ασχοληθώ τώρα, αλλά παρόμοιες έχω απαντήσει πολύ πρόσφατα εδώ: https://ischool.e-steki.gr/showpost.php?p=2395525&postcount=2696 (ωστόσο κανείς δεν είναι υποχρεωμένος να ψάχνει ψύλλους στα άχυρα - δεν ψάχνεις εύκολα και γρήγορα 2700+ μηνύματα)
Όσο για το
Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rose93
Νεοφερμένο μέλος


Και θα τελειώσει στην άλλη του ζωή...
5o: z^2=4|z|-3, άρα ο z είναι πραγματικός. Λύσε απλώς την δευτεροβάθμια εξίσωση.
6ο: |z+1|=-(z+i)=πραγματικός=> z=x-i με χ αρνητικό. Άρα |(χ+1)+(-1)i|=-x και υφώνουμε στο τετράγωνο και βρίσκουμε χ=-1. Άρα z=-1-i
Θα μπορούσαμε επίσης να προχωρήσουμε διαφορετικά:
Να πάρουμε μέτρα στην |z+1|=-(z+i)=> |z+1|=|z+i| και θα προχωρώντας θα βλέπαμε ότι χ=y, θα αντικαθιστούσαμε στην αρχική και θα φτάναμε πάλι σε z=-1-i.
7o: Ίδιο με 6ο.
στο 5ο πως προκυπτει οτι ο z ειναι πραγματικος??
Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
koum
Πολύ δραστήριο μέλος


Το δεύτερο μέλος είναι κι αυτό πραγματικός αριθμός. (στο 5ο πως προκυπτει οτι ο z ειναι πραγματικος??
Για την ακρίβεια ο

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Evi_Panay
Εκκολαπτόμενο μέλος


οποιος μπορει ας με βοηθησει!
Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Evi_Panay
Εκκολαπτόμενο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Dias
Επιφανές μέλος


² --> Alt+Ctrl+2 (ελληνικό πληκτρολόγιο) , | --> Shift+\Να δειξετε οτι, |z+w+u|=2 (1) αν δινεται οτι |zu + uw + wz |=1 (2) και οτι z² + u²+ w² = 0 (3) , |z|=|w|=|u|=1 (4)
Έχει πολλές πράξεις. Θα σου πώ τον τρόπο:
Από (4): |z|² = 1 => z̅ = 1/z κλπ
Παίρνεις το |z+w+u|² να το βγάλεις = 4. Το γραφεις γινόμενο (z+w+u) επί συζυγή, κάνεις πράξεις, χρησιμοποιείς την (4) και βγάζεις = 3 + άλλα. Αυτά τα άλλα με τη βοήθεια των (2) και (3) με πράξεις βγάινουν 1.
(Την έλυσα , βγαίνει, κάντο και συ).

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Evi_Panay
Εκκολαπτόμενο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Dias
Επιφανές μέλος


Μπα. Υπάρχουν πολλές τέτοιες. Και αυτές που έχουν πολλές πράξεις τις βαριέμαι.ευφυεστατη η ασκηση παντως!!!

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Evi_Panay
Εκκολαπτόμενο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Dias
Επιφανές μέλος


........... 2z³z̅ + 5zz̅³ + 7 = 0
(Δεν θέλω να μου τη λύσετε - Υπόδειξη μόνο να ξεκινήσω αν μπορείτε)
Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
koum
Πολύ δραστήριο μέλος


Να βρεθεί ο μιγαδικός αριθμός z που επαληθεύει τη σχέση:
........... 2z³z̅ + 5zz̅³ + 7 = 0
(Δεν θέλω να μου τη λύσετε - Υπόδειξη μόνο να ξεκινήσω αν μπορείτε)

Όλα τα
Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Dias
Επιφανές μέλος


Δεν κατάλαβα την ερώτηση. z ο μιγαδικός που ψάχνουμε και z̅ ο συζυγής του. Τι θα πεί z "μη συζυγείς"?Όλα ταείναι μη συζυγείς μιγαδικοί;

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
koum
Πολύ δραστήριο μέλος


Δεν κατάλαβα την ερώτηση. z ο μιγαδικός που ψάχνουμε και z̅ ο συζυγής του. Τι θα πεί z "μη συζυγείς"?

Στην εκφώνηση που δίνεις, όλοι οι μιγαδικοί είναι
Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Μιχάλης9867
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Dias
Επιφανές μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
koum
Πολύ δραστήριο μέλος


Έχετε δίκιο αν δεν χρησιμοποιείτε Ι.Ε. Τώρα είδα ότι ο Μοντζίλας δεν βγάζει τις παύλες. Να αλλιώς η εκφώνηση με εικόνα:

Λέω και γω...

Ισχύει γενικά ότι:
Οπότε έχουμε:
Συνέχισε...

Ps: Γιατί δεν γράφεις σε latex;

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Dias
Επιφανές μέλος


Κατάλαβα. Αφαιρώ κατά μέλη και βγαίνει:Συνέχισε...
...........
και η συνέχεια παιχνιδάκι. Σ΄ευχαριστώ πάρα πολύ.(


 )³
)³Δεν το έχω χρησιμοποιήσει ποτέ ακόμα το lastex. Δεν το ξέρω και δεν μου αρέσει το γράψιμό του. Ίσως αργότερα. Αααα!! Βγαίνουν και με τον Μοντζίλα τα συμβολά μου αν τα μεγαλώσεις.Ps: Γιατί δεν γράφεις σε latex;
Θενκς ε λοτ εγκαίην!

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
koum
Πολύ δραστήριο μέλος


Κατάλαβα. Αφαιρώ κατά μέλη και βγαίνει:
...........
και η συνέχεια παιχνιδάκι. Σ΄ευχαριστώ πάρα πολύ.()³
Μην ευχαριστείς, κι εσύ το ίδιο θα έκανες.

Δεν το έχω χρησιμοποιήσει ποτέ ακόμα το lastex. Δεν το ξέρω και δεν μου αρέσει το γράψιμό του. Ίσως αργότερα. Αααα!! Βγαίνουν και με τον Μοντζίλα τα συμβολά μου αν τα μεγαλώσεις.
Θενκς ε λοτ εγκαίην!

Δώσ' του μια ευκαιρία πάντως. Άπαξ και το συνηθίσεις δεν θα γυρίσεις στις παύλες και τα βελάκια.

Ps: Με chrome μπαίνω...

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
stavrospc
Νεοφερμένο μέλος


Αν ισχύει αυτό τότε γιατί συμβαίνει αυτό;;;Που κάνω λάθος;;;Να δειξετε οτι, {z+w+u}=2 (μετρο ειναι) αν δινεται οτι {zu + uw + wz }=1 και οτι z^2 + u^2+ w^2=0 , {z}={w}={u}=1
οποιος μπορει ας με βοηθησει!
 :
:|z+w+u|=2 <=> |z+w+u|²=4 <=> |(z+w+u)²|=4 <=> |z² + w² + u² +2zw+2zu+2wu|=4 <=> 2|zw+zu+wu|=4 (αφού z² + w² + u²=0)
άρα <=>|zw+zu+wu|=2 <>1
Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 5 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 227 μέλη διάβασαν αυτό το θέμα:
- hristosdab
- trifasikodiavasma
- haji
- thepigod762
- Mariosm.
- soulatso
- oteletampis
- phleidhs
- Hased Babis
- AggelikiGr
- sir ImPeCaBlE
- veiNqh
- Scandal
- alekos
- Debugging_Demon
- just some guy
- xristosgkm
- ismember
- Apocalypse
- arrow25
- rempelos42
- ggl
- GStef
- QWERTY23
- xrisamikol
- Σωτηρία
- nikoletaz57
- _Aggelos123
- Mariam38
- SlimShady
- strsismos88
- Georgekk
- Lia 2006
- igeorgeoikonomo
- marian
- tsiobieman
- constansn
- Xristosdimitra
- Panagiotis849
- ρενακι 13
- Memetchi
- eukleidhs1821
- Nikkkpat
- Unboxholics
- korlef
- kwstaseL
- Thanos_D
- the purge
- T C
- Giii
- Papachrist
- liaiscool
- Αννα Τσιτα
- globglogabgalab
- Pharmacist01
- thanahss
- abcdefg12345
- nicole1982
- thecrazycretan
- kvstas92
- KingOfPop
- maria301
- papa2g
- stefan
- Κλημεντίνη
- TonyMontanaEse
- Athens2002
- Alexecon1991
- Μάρκος Βασίλης
- Cortes
- το κοριτσι του μαη
- calliope
- ale
- panagiotis G
- Kleanth
- aggelosst9
- BioChemical
- spring day
- nucomer
- Georgia110
- LeoDel
- pink_panther
- Alexandros973
- marsenis
- den antexw allh apotyxia
- KaterinaL
- kiyoshi
- drosos
- Λαμπρινηη
- Bill22
- Chrysablac.
- giorgosp97
- Βλα
- Monster Hunter
- jul25
- xxxtolis
- Stroka
- nicks1999
- totiloz
- Earendil
- mitsakos
- tasost
- lnesb
- ssalex
- Vasilina93
- alan09
- Livaja10
- χημεια4λαιφ
- Viedo
- UncleJ
- Kostakis45
- Infrared
- Zgian
- pepatogourounaki
- hirasawayui
- GeoCommand
- Eleni54
- American Economist
- EiriniS20
- ΘανάσοςG4
- stamoul1s
- Αριάνα123
- uni77
- Libertus
- tasoss
- PanosCh002
- Unseen skygge
- Νικόλας Ραπ.
- cel123
- The Limit Does Not Exist
- don_vito
- suaimhneas
- Αλκης Κ.
- alexrami
- Baggelitsa36
- Νομικάριος13
- spinalgr1990
- d_th
- Adolfo valencia
- Πα.Κ
- Vasilis25
- Johnman97
- Steffie88
- rekcoR
- gwgw_5
- fockos
- Mariahj
- roud
- kostas83
- Cpt.Philips
- Makis45
- Χρησλου
- Panos_02
- Vold
- tymvorixos
- GiorgosAsi
- Neos167
- theodoraooo
- George187
- Άρτεμις Α.
- Μαρία2222
- christos87
- Idontknoww
- jimis2001
- Metamorph
- Γατόπαρδος.
- Johnsk
- mitsos14
- johnsiak
- Elel
- Dreamer_SW
- Γιαννης1987Θεσσ
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

