lowbaper92
Πολύ δραστήριο μέλος


ΈχειςΑν οι εικόνες Α,Β των μιγαδικών z1 k z2 στο μιγαδικο ανηκουν στον ιδιο κυκλο μ κέντρο την αρχή των αξόνων , να αποδείξετε ότι ο μιγαδικος w=[(z1+z2)/(zi-z2)]^2 , z1<>z2 είναι πραγματικός αριθμός
Άρα
Αρκεί
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Pasipoy
Νεοφερμένο μέλος


ημαρτον δεν τ ειδα ευχαριστω αγορινα μΈχεις
Άρα,
Αρκεί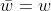
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
koum
Πολύ δραστήριο μέλος


Αν οι εικόνες Α,Β των μιγαδικών z1 k z2 στο μιγαδικο ανηκουν στον ιδιο κυκλο μ κέντρο την αρχή των αξόνων , να αποδείξετε ότι ο μιγαδικος w=[(z1+z2)/(zi-z2)]^2 , z1<>z2 είναι πραγματικός αριθμός
Αρκεί να δείξουμε ότι:
Ισχύει ότι:
Έχουμε:
edit: sorry, άργησα...
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
tsoump
Νεοφερμένο μέλος


Στην 58 σελίδα η άσκηση 10 τα : πέμπτο , έκτο κι έβδομο ερώτημα με δυσκολεύουν. Με το να θέσω τα z βγαίνουν πράξεις του τύπου z^4 .
5ο : z² -4|z| + 3 = 0
6o : z + |z+1| + i = 0
7o: |z| + z = 2 + i
Τα προηγούμενα ερωτήματα μου φάνηκαν εξίσου περίεργα αφού δεν ήταν κάτι που το συναντας συχνά.
Δεν ξέρω τι να κάνω μου 'χουν φάει κοντά στις 2 ώρες....
Αναμένω απάντηση :-)
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
akiroskirios
Δραστήριο μέλος


Εχω κι εγώ κάποιες απορίες στο βοήθημα του μπάρλα.
Στην 58 σελίδα η άσκηση 10 τα : πέμπτο , έκτο κι έβδομο ερώτημα με δυσκολεύουν. Με το να θέσω τα z βγαίνουν πράξεις του τύπου z^4 .
5ο : z² -4|z| + 3 = 0
6o : z + |z+1| + i = 0
7o: |z| + z = 2 + i
Τα προηγούμενα ερωτήματα μου φάνηκαν εξίσου περίεργα αφού δεν ήταν κάτι που το συναντας συχνά.
Δεν ξέρω τι να κάνω μου 'χουν φάει κοντά στις 2 ώρες....
Αναμένω απάντηση :-)
θέσε z=x+ψi και καλό κουράγιο

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


Και θα τελειώσει στην άλλη του ζωή...Αρχική Δημοσίευση από akiroskirios:θέσε z=x+ψi και καλό κουράγιο
5o: z^2=4|z|-3, άρα ο z είναι πραγματικός. Λύσε απλώς την δευτεροβάθμια εξίσωση.Εχω κι εγώ κάποιες απορίες στο βοήθημα του μπάρλα.
Στην 58 σελίδα η άσκηση 10 τα : πέμπτο , έκτο κι έβδομο ερώτημα με δυσκολεύουν. Με το να θέσω τα z βγαίνουν πράξεις του τύπου z^4 .
5ο : z² -4|z| + 3 = 0
6o : z + |z+1| + i = 0
7o: |z| + z = 2 + i
Τα προηγούμενα ερωτήματα μου φάνηκαν εξίσου περίεργα αφού δεν ήταν κάτι που το συναντας συχνά.
Δεν ξέρω τι να κάνω μου 'χουν φάει κοντά στις 2 ώρες....
Αναμένω απάντηση :-)
6ο: |z+1|=-(z+i)=πραγματικός=> z=x-i με χ αρνητικό. Άρα |(χ+1)+(-1)i|=-x και υφώνουμε στο τετράγωνο και βρίσκουμε χ=-1. Άρα z=-1-i
Θα μπορούσαμε επίσης να προχωρήσουμε διαφορετικά:
Να πάρουμε μέτρα στην |z+1|=-(z+i)=> |z+1|=|z+i| και θα προχωρώντας θα βλέπαμε ότι χ=y, θα αντικαθιστούσαμε στην αρχική και θα φτάναμε πάλι σε z=-1-i.
7o: Ίδιο με 6ο.
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
tsoump
Νεοφερμένο μέλος



Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
vavlas
Εκκολαπτόμενο μέλος


Για ποιες τιμές του x,y(οι χ και οι ψ είναι πραγματικοί) ισχύσει η παρακάτω παράσταση.
(2-3i)²-i(x-2iy)=x+yi
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


(2^2-2*3i+(3i)^2)-xi+2iy*i=x+yi => 4-6i-9-xi-2y=x+yi => -5-2y=x and -6-x=y => y=1 and x=-7.Μπορεί να με βοηθήσει κάποιος στην παρακάτω άσκηση;
Για ποιες τιμές του x,y(οι χ και οι ψ είναι πραγματικοί) ισχύσει η παρακάτω παράσταση.
(2-3i)²-i(x-2iy)=x+yi
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
vavlas
Εκκολαπτόμενο μέλος


(2^2-2*3i+(3i)^2)-xi+2iy*i=x+yi => 4-6i-9-xi-2y=x+yi => -5-2y=x and -6-x=y => y=1 and x=-7.
Αυτό,δεν αναπτύσσεται έτσι;
(2-3i)²=(2^2-2*2*3i-3i^2)
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lowbaper92
Πολύ δραστήριο μέλος


Αυτό,δεν αναπτύσσεται έτσι;
(2-3i)²=(2^2-2*2*3i-3i^2)
To β εδώ είναι το 3ι άρα υψώνεται ολόκληρο στο τετράγωνο
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
koum
Πολύ δραστήριο μέλος


Αυτό,δεν αναπτύσσεται έτσι;
(2-3i)²=(2^2-2*2*3i-3i^2)
Για την ακρίβεια είναι:
Άρα:
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
vavlas
Εκκολαπτόμενο μέλος


(α-β)²=α²-2αβ+β²
Εδώ έχουμε (2-3i)².
Άρα α=2 β=3i
Οπότε μας κάνει 4-12i+(3i)²=-5-12i
Κάνω κάπου λάθος;
Γιατί ο φίλος από πάνω έβγαλε -5-6i
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lowbaper92
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
vavlas
Εκκολαπτόμενο μέλος


-5-12i-xi-2y=x+yi
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
akiroskirios
Δραστήριο μέλος


Αφού φτάσουμε εδώ πέρα τι κάνουμε;
-5-12i-xi-2y=x+yi
-5-2y - (12+x)i=x+yi
και επειδή κάθε μιγαδικός γράφεται με μοναδικό τρόπο στη μορφή α+βi ισχύει:
x=-5-2y και y=-12-x
λύνεις το σύστημα με μια απλή αντικατάσταση και είσαι gg
Με λίγα λόγια εξισώνεις πραγματικό με πραγματικό μέρος και φανταστικό με φανταστικό...
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
vavlas
Εκκολαπτόμενο μέλος


-5-2y - (12+x)i=x+yi
και επειδή κάθε μιγαδικός γράφεται με μοναδικό τρόπο στη μορφή α+βi ισχύει:
x=-5-2y και y=-12-x
λύνεις το σύστημα με μια απλή αντικατάσταση και είσαι gg
Με λίγα λόγια εξισώνεις πραγματικό με πραγματικό μέρος και φανταστικό με φανταστικό...
Άψογος!
Ευχαριστώ πολύ!

Κάποιος σε αυτή εδώ;
Δεν μπορώ να βρω λύση.
z+(z/1-i)=(1+i)³
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
koum
Πολύ δραστήριο μέλος


Κάποιος σε αυτή εδώ;
Δεν μπορώ να βρω λύση.
z+z/1-i=(1+i)³
Έστω
Κλπ...
Y.γ.
και
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Arthur39432
Νεοφερμένο μέλος


|z|² = - z
Η απαντηση ειναι z=λi με λ
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 1 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 232 μέλη διάβασαν αυτό το θέμα:
- Hased Babis
- ChrisG152
- giorgos5002
- giannis06
- Panagiwths12
- mikke
- hristosdab
- trifasikodiavasma
- haji
- thepigod762
- Mariosm.
- soulatso
- oteletampis
- phleidhs
- AggelikiGr
- sir ImPeCaBlE
- veiNqh
- Scandal
- alekos
- Debugging_Demon
- just some guy
- xristosgkm
- ismember
- Apocalypse
- arrow25
- rempelos42
- ggl
- GStef
- QWERTY23
- xrisamikol
- Σωτηρία
- nikoletaz57
- _Aggelos123
- Mariam38
- SlimShady
- strsismos88
- Georgekk
- Lia 2006
- igeorgeoikonomo
- marian
- tsiobieman
- constansn
- Xristosdimitra
- Panagiotis849
- ρενακι 13
- Memetchi
- eukleidhs1821
- Nikkkpat
- Unboxholics
- korlef
- kwstaseL
- Thanos_D
- the purge
- T C
- Giii
- Papachrist
- liaiscool
- Αννα Τσιτα
- globglogabgalab
- Pharmacist01
- otinanai123
- abcdefg12345
- nicole1982
- thecrazycretan
- kvstas92
- KingOfPop
- maria301
- papa2g
- stefan
- Κλημεντίνη
- TonyMontanaEse
- Lathy
- Alexecon1991
- Μάρκος Βασίλης
- Cortes
- το κοριτσι του μαη
- calliope
- ale
- panagiotis G
- Kleanth
- aggelosst9
- BioChemical
- spring day
- nucomer
- Georgia110
- LeoDel
- pink_panther
- Alexandros973
- marsenis
- den antexw allh apotyxia
- KaterinaL
- kiyoshi
- drosos
- Λαμπρινηη
- Bill22
- Chrysablac.
- giorgosp97
- Βλα
- Monster Hunter
- jul25
- xxxtolis
- Stroka
- nicks1999
- totiloz
- Earendil
- mitsakos
- tasost
- lnesb
- ssalex
- alan09
- Livaja10
- χημεια4λαιφ
- Viedo
- UncleJ
- Kostakis45
- Infrared
- Zgian
- pepatogourounaki
- hirasawayui
- GeoCommand
- Eleni54
- American Economist
- EiriniS20
- ΘανάσοςG4
- stamoul1s
- Αριάνα123
- uni77
- Libertus
- tasoss
- PanosCh002
- Unseen skygge
- Νικόλας Ραπ.
- cel123
- The Limit Does Not Exist
- don_vito
- suaimhneas
- Αλκης Κ.
- alexrami
- Baggelitsa36
- Νομικάριος13
- spinalgr1990
- d_th
- Adolfo valencia
- Πα.Κ
- Vasilis25
- Johnman97
- Steffie88
- rekcoR
- gwgw_5
- fockos
- Mariahj
- roud
- kostas83
- Cpt.Philips
- Makis45
- Χρησλου
- Panos_02
- Vold
- tymvorixos
- GiorgosAsi
- Neos167
- theodoraooo
- George187
- Άρτεμις Α.
- Μαρία2222
- christos87
- Idontknoww
- jimis2001
- Metamorph
- Γατόπαρδος.
- Johnsk
- mitsos14
- johnsiak
- Elel
- Dreamer_SW
- Γιαννης1987Θεσσ
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki



