eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει απο Καινούργιο (Ηράκλειο). Έχει γράψει 3,928 μηνύματα.

20-07-20

12:09
Λενε οτι γινεται καλη δουλεια.Ισχυει?
nPb
Επιφανές μέλος
Ο nPb αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Μεταπτυχιούχος και μας γράφει απο Πάτρα (Αχαΐα). Έχει γράψει 20,984 μηνύματα.

20-07-20

15:08
Nαι αλλά δεν βγαίνεις γιατρός όπως στο ΕΚΠΑ ΤΗΣ ΝΕΑΣ ΥΟΡΚΗΣ από τα Lidl...ωππ, σε λάθος θέμα μπήκα. 

eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει απο Καινούργιο (Ηράκλειο). Έχει γράψει 3,928 μηνύματα.

20-07-20

15:21
ξαναλεω μου εχουν μεταφερει οτι γινεται εξαιρετικη δουλεια σε αυτο το τμημα για αυτο ρωτησα
nPb
Επιφανές μέλος
Ο nPb αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Μεταπτυχιούχος και μας γράφει απο Πάτρα (Αχαΐα). Έχει γράψει 20,984 μηνύματα.

20-07-20

19:08
Για να απαντήσω σοβαρά. Το Τμήμα Μαθηματικών Ιωαννίνων και Πατρών έχουν μια παράλληλη ιστορία και προσέγγιση της Μαθηματικής επιστήμης. Ιδρύθηκαν το μακρινό 1960-66 με σκοπό να καλύψουν νέους τομείς των Μαθηματικών στην μετεμφυλιακή Ελλάδα σύμφωνα με την επανάσταση στον χώρο των Υπολογιστικών Μαθηματικών που συνέβη τη δεκαετία του 1960 με τον κύριο εκπρόσωπο John Von Neumann και μετέπειτα συνεχιστές Donald Knuth, Amijo και άλλους. Η κρατική απάντηση ήταν να καλύψει ατέλειες και αδυναμίες των παλαιότερων Τμημάτων Μαθηματικών Αθήνας και Θεσσαλονίκης.
Έτσι το Τμήμα αυτό εκτός από τον κύριο τομέα των καθαρών μαθηματικών προσφέρει:
Οι συγκεκριμένοι προαναφερθέντες τομείς καλύπτονται κλασικά από Τμήματα Εφαρμοσμένων Μαθηματικών ενώ απαιτούν πολύ καλό υπόβαθρο και εξοικείωση με καθαρά μαθηματικά ειδικά της Ανάλυσης (Διαφορικού Λογισμού) σε συνδυασμό με προγραμματισμό (γραφή κώδικα). Γενικά στην Ελλάδα, ο πανίσχυρος κλάδος της Μαθηματικής μοντελοποίησης δεν χαίρει εκτίμησης λόγω κακής Μαθηματικής παιδείας υποβάθρου. Συνήθως οι μαθητές που εισέρχονται σε ένα Μαθηματικό Τμήμα λόγω χαμηλών βαθμών στα Μαθηματικά, αποφεύγουν μαζικά να επιλέγουν μαθήματα ειδικού Μαθηματικού ενδιαφέροντος και μένουν σε αοριστολογίες γύρω από την θεωρητική Πληροφορική.
Έτσι το Τμήμα αυτό εκτός από τον κύριο τομέα των καθαρών μαθηματικών προσφέρει:
- τομέα Μαθηματικής Ανάλυσης με θεματική ειδίκευση στην Συναρτησιακή Ανάλυση, Ολοκληρωτικές Εξισώσεις, Κυρτή Γεωμετρία και Μερικές Διαφορικές Εξισώσεις
- τομέα Εφαρμοσμένων Μαθηματικών και Μηχανικής Έρευνας με θεματική ειδίκευση στην Υπολογιστική Μηχανική Ρευστών, Μη Γραμμική Κυματική / Οπτική, Αριθμητική Ανάλυση και High-Performance Computing (Γεωμετρία Πλεγματικών προτύπων κλπ)
Οι συγκεκριμένοι προαναφερθέντες τομείς καλύπτονται κλασικά από Τμήματα Εφαρμοσμένων Μαθηματικών ενώ απαιτούν πολύ καλό υπόβαθρο και εξοικείωση με καθαρά μαθηματικά ειδικά της Ανάλυσης (Διαφορικού Λογισμού) σε συνδυασμό με προγραμματισμό (γραφή κώδικα). Γενικά στην Ελλάδα, ο πανίσχυρος κλάδος της Μαθηματικής μοντελοποίησης δεν χαίρει εκτίμησης λόγω κακής Μαθηματικής παιδείας υποβάθρου. Συνήθως οι μαθητές που εισέρχονται σε ένα Μαθηματικό Τμήμα λόγω χαμηλών βαθμών στα Μαθηματικά, αποφεύγουν μαζικά να επιλέγουν μαθήματα ειδικού Μαθηματικού ενδιαφέροντος και μένουν σε αοριστολογίες γύρω από την θεωρητική Πληροφορική.
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει απο Καινούργιο (Ηράκλειο). Έχει γράψει 3,928 μηνύματα.

20-07-20

19:27
το θεμα ειναι γτ να ασχολειται σε ενα μαθηματικο με θεωρητικη πληροφορικη.ας πηγαινε σε πληροφορικης τμημα.επιτελους ενα ωραια μηνυμα σου χωρις γενικολογιες
nPb
Επιφανές μέλος
Ο nPb αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Μεταπτυχιούχος και μας γράφει απο Πάτρα (Αχαΐα). Έχει γράψει 20,984 μηνύματα.

20-07-20

19:55
Eυκλείδη από την μικρή μου εμπειρία θα σου πω το εξής. Οι Μαθηματικοί στην Ελλάδα έχουν μια κακή εικόνα των Μαθηματικών στο μυαλό τους και μια ασάφεια ως προς τι σημαίνει Πληροφορική. Πιο συγκεκριμένα θα σου αντιπαραβάλω δυο περιγραφές:
Η Θεωρητική Πληροφορική με έμφαση στην Θεωρία Αυτομάτων, Λογικό Σχεδιασμό και Διακριτά Μαθηματικά αφορά κυρίως τον προγραμματισμό της μνήμης του υπολογιστή γι' αυτό και χρησιμοποιούνται μαθήματα με γλώσσες C/C++, Java κλπ. Το 99% των Μαθηματικών στην Ελλάδα έχουν μια άποψη ότι η εφαρμογή των Μαθηματικών στην Πληροφορική είναι μόνο αυτή.
Η Αριθμητική Ανάλυση με έμφαση στην Θεωρία Προσέγγισης Λύσεων, Διαφορικών Εξισώσεων, Μη Γραμμικών Αλγεβρικών Συστημάτων και Νευρωνικών Δικτύων αφορά κυρίως τον προγραμματισμό σε δεύτερο επίπεδο. Το πρώτο επίπεδο είναι η διατύπωση του Μαθηματικού Μοντέλου μέσω επιλογής κατάλληλου τύπου εξισώσεων καθώς και της θεωρηματικής ανάλυσής τους (γεωμετρία λύσεων, συγκλίσεις κλπ) ή και τη χρήση τεχνικών βελτιστοποίησης μέσω Λογισμού Μεταβολών. Το δεύτερο επίπεδο είναι η προσαρμογή σε κάποιο εφαρμοσμένο πρόβλημα Μηχανικών Διεργασιών (π.χ. η διάδοση ενός θαλασσίου κύματος) και την αριθμητική επίλυσή του μέσω προγραμματισμού. Ο προγραμματισμός εδώ δεν έχει σχέση με λογικές πύλες όσο με διακριτά σχήματα, γραφήματα πολύπλοκης όψης και εντολές επανάληψης. Θέλει τόσο τη μαθηματική ικανότητα σε θεωρηματική βάση όσο και την ιδιοφυϊα κατανόησης πως λειτουργεί το διακριτό σχήμα στον αλγόριθμο καθώς και τι εκφράζει ποιοτικά το γράφημα ή η λίστα αριθμητικών τιμών (αριθμητική κινητής υποδιαστολής) με βάση αυτό που μας διατυπώνει το θεώρημα ή η μαθηματική θεωρία πάντα. Στην άποψη αυτή δεν έχω βρει καμία συμπάθεια από τους Έλληνες Μαθηματικούς και το αστείο είναι ότι η στρογγυλοποίηση αριθμών είναι πιο Μαθηματικό ζήτημα από την γεννήτρια αριθμών. Συνήθως όσοι φοιτητές σπουδάζουν στο Μαθηματικό μισούν κατά κάποιο τρόπο την Φυσική ή την Μαθηματική Μηχανική επειδή απαιτεί σελίδες γραφής αυστηρών μαθηματικών σκέψεων.
Ως προς την δεύτερη άποψη, οι Μαθηματικοί κινούνται προς Στατιστική ή Οικονομικά σε ασαφή μονοπάτια. Επίσης αναφέρω ότι σε πολλά σημεία η Στατιστική με την Αριθμητική Ανάλυση έχουν κοινή μαθηματική διαδρομή.
Η Θεωρητική Πληροφορική με έμφαση στην Θεωρία Αυτομάτων, Λογικό Σχεδιασμό και Διακριτά Μαθηματικά αφορά κυρίως τον προγραμματισμό της μνήμης του υπολογιστή γι' αυτό και χρησιμοποιούνται μαθήματα με γλώσσες C/C++, Java κλπ. Το 99% των Μαθηματικών στην Ελλάδα έχουν μια άποψη ότι η εφαρμογή των Μαθηματικών στην Πληροφορική είναι μόνο αυτή.
Η Αριθμητική Ανάλυση με έμφαση στην Θεωρία Προσέγγισης Λύσεων, Διαφορικών Εξισώσεων, Μη Γραμμικών Αλγεβρικών Συστημάτων και Νευρωνικών Δικτύων αφορά κυρίως τον προγραμματισμό σε δεύτερο επίπεδο. Το πρώτο επίπεδο είναι η διατύπωση του Μαθηματικού Μοντέλου μέσω επιλογής κατάλληλου τύπου εξισώσεων καθώς και της θεωρηματικής ανάλυσής τους (γεωμετρία λύσεων, συγκλίσεις κλπ) ή και τη χρήση τεχνικών βελτιστοποίησης μέσω Λογισμού Μεταβολών. Το δεύτερο επίπεδο είναι η προσαρμογή σε κάποιο εφαρμοσμένο πρόβλημα Μηχανικών Διεργασιών (π.χ. η διάδοση ενός θαλασσίου κύματος) και την αριθμητική επίλυσή του μέσω προγραμματισμού. Ο προγραμματισμός εδώ δεν έχει σχέση με λογικές πύλες όσο με διακριτά σχήματα, γραφήματα πολύπλοκης όψης και εντολές επανάληψης. Θέλει τόσο τη μαθηματική ικανότητα σε θεωρηματική βάση όσο και την ιδιοφυϊα κατανόησης πως λειτουργεί το διακριτό σχήμα στον αλγόριθμο καθώς και τι εκφράζει ποιοτικά το γράφημα ή η λίστα αριθμητικών τιμών (αριθμητική κινητής υποδιαστολής) με βάση αυτό που μας διατυπώνει το θεώρημα ή η μαθηματική θεωρία πάντα. Στην άποψη αυτή δεν έχω βρει καμία συμπάθεια από τους Έλληνες Μαθηματικούς και το αστείο είναι ότι η στρογγυλοποίηση αριθμών είναι πιο Μαθηματικό ζήτημα από την γεννήτρια αριθμών. Συνήθως όσοι φοιτητές σπουδάζουν στο Μαθηματικό μισούν κατά κάποιο τρόπο την Φυσική ή την Μαθηματική Μηχανική επειδή απαιτεί σελίδες γραφής αυστηρών μαθηματικών σκέψεων.
Ως προς την δεύτερη άποψη, οι Μαθηματικοί κινούνται προς Στατιστική ή Οικονομικά σε ασαφή μονοπάτια. Επίσης αναφέρω ότι σε πολλά σημεία η Στατιστική με την Αριθμητική Ανάλυση έχουν κοινή μαθηματική διαδρομή.
nPb
Επιφανές μέλος
Ο nPb αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Μεταπτυχιούχος και μας γράφει απο Πάτρα (Αχαΐα). Έχει γράψει 20,984 μηνύματα.

21-07-20

13:16
Mια εικόνα πως οι Έλληνες Μαθηματικοί αντιλαμβάνονται τη χρησιμότητα της Πληροφορικής στα Μαθηματικά.

Μια εικόνα όπως η Πληροφορική δίνει λύσεις σε προβλήματα των Μαθηματικών στον πραγματικό κόσμο της Επιστήμης, μέσω της Αριθμητικής Ανάλυσης που οι Έλληνες Μαθηματικοί δεν επιθυμούν για λόγους υποβάθρου - μαθηματικής αγραμματοσύνης (μπαίνουν με βαθμό 8-12 στις πανελλήνιες στα Μαθηματικά), βλακείας και ιδεολογικής στασιμότητας.
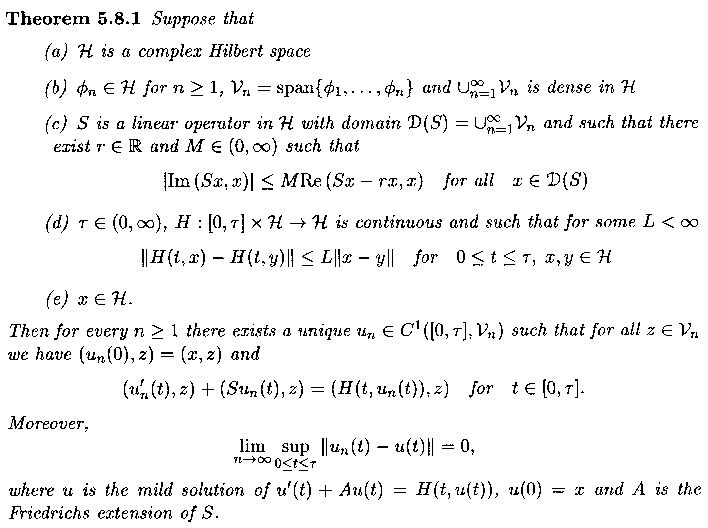
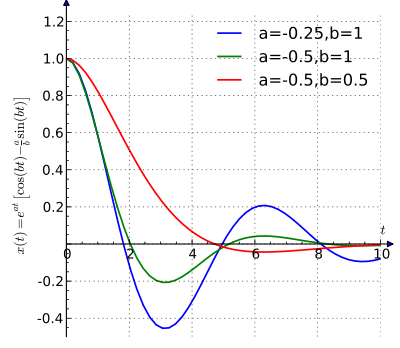
και η Μαθηματική προσομοίωση κυματικής μεταφοράς σε 2 διαστάσεις (πατήστε). Η πρώτη εικόνα με το θεώρημα είναι από τον χώρο της Ανάλυσης Τελεστών για προβλήματα εξέλιξης μερικών διαφορικών εξισώσεων που αποτελεί κύριο πεδίο έρευνας των σύγχρονων Εφαρμοσμένων Μαθηματικών με διαφορετικό βαθμό "θεωρητικής" προσέγγισης. Η δεύτερη εικόνα είναι από τον χώρο των μηχανικών ταλαντώσεων κάποιου μη αυτόνομου δυναμικού συστήματος στη 1 χωρική διάσταση. Το διεθνές πεδίο έρευνας ανήκει στην Μαθηματική Θεωρία της Κλασικής Μηχανικής και Δυναμικών Συστημάτων, που αποτελεί το ευρύτερο χώρο έρευνας των Εφαρμοσμένων Μαθηματικών για την Γεωμετρία και Ανάλυση Λύσεων για Διαφορικές Εξισώσεις. Η δεύτερη εικόνα και ο σύνδεσμος αποτελούν εφαρμογές μέσω κάποιου προγραμματισμού με κανονικά δεδομένα.
Ποια είναι η άποψη σύγχρονων Ελλήνων Μαθηματικών (καθηγητών μέσης εκπαίδευσης); Πήγαινε φίλε μου και κάνε κάτι στην Πληροφορική (επειδή αυτό πουλάει) για να τα μαζέψεις με την κουτάλα τα φράγκα. Έτσι δεν λένε;

Μια εικόνα όπως η Πληροφορική δίνει λύσεις σε προβλήματα των Μαθηματικών στον πραγματικό κόσμο της Επιστήμης, μέσω της Αριθμητικής Ανάλυσης που οι Έλληνες Μαθηματικοί δεν επιθυμούν για λόγους υποβάθρου - μαθηματικής αγραμματοσύνης (μπαίνουν με βαθμό 8-12 στις πανελλήνιες στα Μαθηματικά), βλακείας και ιδεολογικής στασιμότητας.
και η Μαθηματική προσομοίωση κυματικής μεταφοράς σε 2 διαστάσεις (πατήστε). Η πρώτη εικόνα με το θεώρημα είναι από τον χώρο της Ανάλυσης Τελεστών για προβλήματα εξέλιξης μερικών διαφορικών εξισώσεων που αποτελεί κύριο πεδίο έρευνας των σύγχρονων Εφαρμοσμένων Μαθηματικών με διαφορετικό βαθμό "θεωρητικής" προσέγγισης. Η δεύτερη εικόνα είναι από τον χώρο των μηχανικών ταλαντώσεων κάποιου μη αυτόνομου δυναμικού συστήματος στη 1 χωρική διάσταση. Το διεθνές πεδίο έρευνας ανήκει στην Μαθηματική Θεωρία της Κλασικής Μηχανικής και Δυναμικών Συστημάτων, που αποτελεί το ευρύτερο χώρο έρευνας των Εφαρμοσμένων Μαθηματικών για την Γεωμετρία και Ανάλυση Λύσεων για Διαφορικές Εξισώσεις. Η δεύτερη εικόνα και ο σύνδεσμος αποτελούν εφαρμογές μέσω κάποιου προγραμματισμού με κανονικά δεδομένα.
Ποια είναι η άποψη σύγχρονων Ελλήνων Μαθηματικών (καθηγητών μέσης εκπαίδευσης); Πήγαινε φίλε μου και κάνε κάτι στην Πληροφορική (επειδή αυτό πουλάει) για να τα μαζέψεις με την κουτάλα τα φράγκα. Έτσι δεν λένε;

VouDou
Πολύ δραστήριο μέλος
Ο Δημήτριος αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 49 ετών, Καθηγητής και μας γράφει απο Κυπαρισσία (Μεσσηνία). Έχει γράψει 1,365 μηνύματα.

21-07-20

13:52
Το ίδιο του Υπ. Παιδείας αντιλαμβάνεται την πληροφορική ως εφαρμογές στα οικονομικά (που τα έβαλε στο 4ο πεδίο)... δηλαδή τα εφαρμοσμένης πληροφορικής που υπήρχαν πρώτα σε ΟΠΑ και ΠΑΜΑΚ. Φυσικά τα έβαλε για να "γεμίσει" το εν λόγω πεδίο, αφού τις ψυχολογίες-κοινωνιολογίες-πολιτικές επιστήμες κ.λπ. τα έβαλε μόνο στο 1ο πεδίο (τα οικονομικά είναι μια κοινωνική επιστήμη).
Τα άλλα τμήματα πληροφορικής (το σκέτο) το αντιλαμβάνονται ως Καθηγητές ΔΕ (πρώτα, έμπαιναν εκεί άτομα με το σχετικό σεμινάριο 400 ωρών)! Στα παλιότερα μηχανογραφικά ήταν στην "ουρά" της λίστας των μαθηματικών-φυσικών-χημικών κ.λπ. καθηγητικών σχολών θετικής κατεύθυνσης (κάποτε τα τμήματα δεν ήταν αλφαβητικά στο μηχανογραφικό).
Ο κλάδος της πληροφορικής, όπως έχουμε αναφέρει και παλιότερα, δεν έχει κατοχυρωμένα επαγγελματικά δικαιώματα. Οι μηχανικοί Η/Υ πήγαν (και ανήκουν) στο 2ο πεδίο και εκεί "τράβηξαν" και τα τμήματα πληροφορικής (σκέτο) να υπάρχουν, επίσης συμπληρωματικά.
Η πληροφορική, ως κλάδος, είναι κλάδος των μαθηματικών, τα οποία μαθηματικά είναι κλάδος (πολύ παλιά) της φιλοσοφίας! Αυτό στην ιστορική εξέλιξη των αυτών επιστημών (βασικά, η επιστήμη είναι μία)!
Στα μαθηματικά (πρωτοδεσμίτης) πάντα με εκνεύριζε (και δυσκολία τους, κυρίως στη γεωμετρία) το "έστω"! Τί έστω; να μυρίσω τα νύχια μου; (για αυτό είχα αγαπημένο μάθημα τη φυσικοχημεία).
Τα άλλα τμήματα πληροφορικής (το σκέτο) το αντιλαμβάνονται ως Καθηγητές ΔΕ (πρώτα, έμπαιναν εκεί άτομα με το σχετικό σεμινάριο 400 ωρών)! Στα παλιότερα μηχανογραφικά ήταν στην "ουρά" της λίστας των μαθηματικών-φυσικών-χημικών κ.λπ. καθηγητικών σχολών θετικής κατεύθυνσης (κάποτε τα τμήματα δεν ήταν αλφαβητικά στο μηχανογραφικό).
Ο κλάδος της πληροφορικής, όπως έχουμε αναφέρει και παλιότερα, δεν έχει κατοχυρωμένα επαγγελματικά δικαιώματα. Οι μηχανικοί Η/Υ πήγαν (και ανήκουν) στο 2ο πεδίο και εκεί "τράβηξαν" και τα τμήματα πληροφορικής (σκέτο) να υπάρχουν, επίσης συμπληρωματικά.
Η πληροφορική, ως κλάδος, είναι κλάδος των μαθηματικών, τα οποία μαθηματικά είναι κλάδος (πολύ παλιά) της φιλοσοφίας! Αυτό στην ιστορική εξέλιξη των αυτών επιστημών (βασικά, η επιστήμη είναι μία)!
Στα μαθηματικά (πρωτοδεσμίτης) πάντα με εκνεύριζε (και δυσκολία τους, κυρίως στη γεωμετρία) το "έστω"! Τί έστω; να μυρίσω τα νύχια μου; (για αυτό είχα αγαπημένο μάθημα τη φυσικοχημεία).
Μάρκος Βασίλης
Πολύ δραστήριο μέλος
Ο Βασίλης αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 28 ετών, Διδακτορικός και μας γράφει απο Καισαριανή (Αττική). Έχει γράψει 1,871 μηνύματα.

21-07-20

14:06
@nPb Η εικόνα που έχεις για την αριθμητική ανάλυση και την προτίμηση που (δεν) της δείχνουν νομίζω ότι είναι ψευδής, τουλάχιστον σε ό,τι αφορά το τμήμα Μαθηματικών στην Αθήνα, όπου οι Αριθμητικές Αναλύσεις Ι και ΙΙ (η ΙΙ πλέον καταργήθηκε σχεδόν) ήταν από τα μαθήματα του εφαρμοσμένου καταλόγου με πολύ μεγάλη ζήτηση παρά το ότι ο καθηγητής του μαθήματος - διαχρονικά ο ίδιος - είναι ιδιαίτερα τσεκουράτος στις βαθμολογίες του. Αντιθέτως, κάτι μαθήματα όπως «Αυτόματα και τυπικές γλώσσες» μάζευαν 5 άτομα - πέρα από την πρώτη εβδομάδα που μαζευόταν πολύς κόσμος για να δει τι είναι το μάθημα. Και στην εξέταση άντε να ήταν 10-15. Νιώθω ότι η εικόνα που παρουσιάζεις είναι αρκετά χρόνια πριν και όχι αυτό που επικρατεί σήμερα - τουλάχιστον όχι τα τελευταία 5-6 χρόνια.
@VouDou Διαφωνώ μόνο ως προς την εκπόρευση των μαθηματικών από τη φιλοσοφία. Η αφηρημένη συγκρότηση και η δομή των κλάδων που ασχολούνται με τα μέτα-μαθηματικά αντικείμενα είναι αυτή που έχει επηρεαστεί κι έχει επηρεάσει τη φιλοσοφία, ωστόσο η ίδια η επιστήμη εκπορεύεται από την καθημερινή εμπειρία του ανθρώπου, και στην πορεία της μόνη συναντά τη φιλοσοφία και από εκεί και μετά αλληλεπιδρούν στενά η μία με την άλλη. Άλλη κουβέντα αυτή, βέβαια, αλλά είπα να το αναφέρω μιας και το έθιξες.
@VouDou Διαφωνώ μόνο ως προς την εκπόρευση των μαθηματικών από τη φιλοσοφία. Η αφηρημένη συγκρότηση και η δομή των κλάδων που ασχολούνται με τα μέτα-μαθηματικά αντικείμενα είναι αυτή που έχει επηρεαστεί κι έχει επηρεάσει τη φιλοσοφία, ωστόσο η ίδια η επιστήμη εκπορεύεται από την καθημερινή εμπειρία του ανθρώπου, και στην πορεία της μόνη συναντά τη φιλοσοφία και από εκεί και μετά αλληλεπιδρούν στενά η μία με την άλλη. Άλλη κουβέντα αυτή, βέβαια, αλλά είπα να το αναφέρω μιας και το έθιξες.
VouDou
Πολύ δραστήριο μέλος
Ο Δημήτριος αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 49 ετών, Καθηγητής και μας γράφει απο Κυπαρισσία (Μεσσηνία). Έχει γράψει 1,365 μηνύματα.

21-07-20

14:13
@VouDou Διαφωνώ μόνο ως προς την εκπόρευση των μαθηματικών από τη φιλοσοφία. Η αφηρημένη συγκρότηση και η δομή των κλάδων που ασχολούνται με τα μέτα-μαθηματικά αντικείμενα είναι αυτή που έχει επηρεαστεί κι έχει επηρεάσει τη φιλοσοφία, ωστόσο η ίδια η επιστήμη εκπορεύεται από την καθημερινή εμπειρία του ανθρώπου, και στην πορεία της μόνη συναντά τη φιλοσοφία και από εκεί και μετά αλληλεπιδρούν στενά η μία με την άλλη. Άλλη κουβέντα αυτή, βέβαια, αλλά είπα να το αναφέρω μιας και το έθιξες.
[/QUOTE]
Και όμως έτσι ξέρω ότι ήταν (όχι στο σήμερα). Κάποτε (πριν πολλά χρόνια), το μαθηματικό ήταν στη φιλοσοφική σχολή (π.χ. λογικός στοχασμός) και μετά "ξεχώρισε".

 www.math.uoa.gr
www.math.uoa.gr
[/QUOTE]
Και όμως έτσι ξέρω ότι ήταν (όχι στο σήμερα). Κάποτε (πριν πολλά χρόνια), το μαθηματικό ήταν στη φιλοσοφική σχολή (π.χ. λογικός στοχασμός) και μετά "ξεχώρισε".

Ιστορικά στοιχεία
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 1 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 67 μέλη διάβασαν αυτό το θέμα:
- panosT436
- Hased Babis
- tsiribim-tsiribom
- Stergios
- Kolimpri
- Scandal
- ale
- ggl
- Jimmy20
- pink_panther
- indecisive
- carnage
- lnesb
- panagiotis23
- VouDou
- azula
- cel123
- Thanos_D
- T C
- Unseen skygge
- eukleidhs1821
- Athens2002
- tsiobieman
- Viedo
- Yiorgosk
- Marianna35
- ΘανάσοςG4
- Μάρκος Βασίλης
- J.Cameron
- eri548
- kostas83
- Trolling Stones
- Ggpg
- Αλκης Κ.
- Monster Hunter
- don_vito
- tasost
- Kostakis45
- MarcoReus
- Belle26
- EiriniS20
- fmarulezkd
- victor 21
- Meow
- Dababy
- Ireneeneri
- Johanna Mark
- kiyoshi
- Μαρία234
- the purge
- Kostis-Palamas
- Stelios725
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

