Συλλογή ασκήσεων και τεστ στα Μαθηματικά Προσανατολισμού

ledzeppelinick · 08-05-09

αχχχ.. με προλαβε ο βασιλης για την πρωτη... πολυ σωστος ο φιλος απο ροδο νομιζω και για την δευτερη!! οπως και να χει ανεβαζω την 1η πολυ αναλυτικα

ledzeppelinick · 08-05-09

εμ.. το τελευταιο πως το δειχνουμε?? κολλησα..:thanks:

manos66 · 09-05-09

Αρχική Δημοσίευση από ledzeppelinick:
αχχχ.. με προλαβε ο βασιλης για την πρωτη... πολυ σωστος ο φιλος απο ροδο νομιζω και για την δευτερη!! οπως και να χει ανεβαζω την 1η πολυ αναλυτικα

To μόνο "λαθάκι" είναι ότι ο γ.τ. είναι έλλειψη και όχι υπερβολή

ledzeppelinick · 09-05-09

ναι συγγνωμη λαθος βιασυνης.. απλα αν εχουμε ελλειψη πρεπει οντως να αναφερουμε ολα αυτα τα στοιχεια που μαθαμε στη δευτερα?? ευχαριστω!

Undead · 09-05-09

Μια απόδειξη για το :αν $f(x)>0$ και $\int_{a}^{b}f(x)dx=0$ τότε $a=b$

αν θεωρήσουμε $F(x)=\int_{a}^{x}f(t)dt$ τότε

$F^{\prime}(x)=f(x)>0$ άρα $F$ είναι γν. αύξουσα άρα και 1-1

άρα $\int_{a}^{b}f(x)dx=0 \Leftrightarrow F(a)=F(b) \Leftrightarrow a=b$

Civilara · 09-05-09

M(4,2) όπου f(4)=2

Η ελάχιστη απόσταση είναι mind=d(4)=SQRT(17)/2

Civilara · 09-05-09

Αρχική Δημοσίευση από riemann80:
απο το βιβλιο "ολοκληρωματα" του δ.νταβου αντιγραφω μια πολυ ωραια ασκηση.

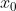
εστω f παραγωγισιμη στο [α,α+3] για την οποια υποθετουμε οτι ισχυει $int_{a}^{a+2}f(x)dx=int_{a+1}^{a+3}f(x)dx$ .να δειξετε οτι υπαρχει $x_0$ στο (α,α+3) ωστε η εφαπτομενη της στο $(x_0,f(x_0))$ να ειναι παραλληλη στον αξονα x.

Στα παρακάτω με S(α,β)f(x)dx συμβολίζω το ορισμένο ολοκλήρωμα της f με κάτω όριο ολοκλήρωσης το α και πάνω το β. Όπου γράφω ΘΜΤΟΛ σημαίνει θεώρημα μέσης τιμής ολοκληρωτικού λογισμού. Αν είναι εκτός ύλης πρέπει να αποδειχτεί. Η απόδειξη είναι απλή και υπάρχει στο βιβλίο. Για λόγους πληρότητας την γράφω μετά τη λύση της άσκησης.

f παραγωγίσιμη [α,α+3] -> f συνεχής [α,α+3]

Από εκφώνηση έχουμε S(α,α+2)f(x)dx=S(α+1,α+3)f(x)dx ->

-> S(α,α+2)f(x)dx=S(α+1,α+2)f(x)dx+S(α+2,α+3)f(x)dx ->
-> S(α,α+2)f(x)dx=-S(α+2,α+1)f(x)dx+S(α+2,α+3)f(x)dx ->
-> S(α,α+2)f(x)dx+S(α+2,α+1)f(x)dx=S(α+2,α+3)f(x)dx ->
-> S(α,α+1)f(x)dx=S(α+2,α+3)f(x)dx

Θέτω S(α,α+1)f(x)dx=S(α+2,α+3)f(x)dx=I

f συνεχής στο [α,α+1] -> ΘΜΤΟΛ: υπάρχει ξ1 στο (α,α+1) ώστε f(ξ1)=S(α,α+1)f(x)=Ι

f συνεχής στο [α+2,α+3] -> ΘΜΤΟΛ :υπάρχει ξ2 στο (α+2,α+3) ώστε f(ξ2)=S(α+2,α+3)f(x)=Ι

Άρα f(ξ1)=f(ξ2)=I και προφανώς α<ξ1<α+1<α+2<ξ2<α+3

f συνεχής στο [ξ1,ξ2], f παραγωγίσιμη στο (ξ1,ξ2) και f(ξ1)=f(ξ2) ->

-> Θεώρημα Rolle : υπάρχει x0 στο (ξ1,ξ2) ώστε f΄(x0)=0

Εξίσωση εφαπτομένης στο Α(x0,f(x0))

y-f(x0)=f΄(x0)(x-x0) -> y=f΄(x0)x+f(x0)-x0f΄(x0) -> y=f(x0) παράλληλη στον άξονα x

ΑΠΟΔΕΙΞΗ ΘΕΩΡΗΜΑΤΟΣ ΜΕΣΗΣ ΤΙΜΗΣ ΟΛΟΚΛΗΡΩΤΙΚΟΥ ΛΟΓΙΣΜΟΥ

Θεώρημα: Αν μία συνάρτηση f είναι συνεχής στο διάστημα [α,β] (α<β) τότε υπάρχει τουλάχιστον ένα ξ στο διάστημα (α,β) τέτοιο ώστε f(ξ)=S(α,β)f(t)dt/(β-α)

Επειδή η f είναι συνεχής στο [α,β], τότε η F με τύπο F(x)=S(α,x)f(t)dt είναι παραγωγίσιμη και συνεπώς και συνεχής στο [α,β] με πρώτη παράγωγο F΄(x)=f(x) για κάθε x στο [α,β]

F(α)=S(α,α)f(t)dt=0
F(β)=S(α,β)f(t)dt

F συνεχής στο [α,β] και παραγωγίσιμη στο (α,β), οπότε σύμφωνα με το θεώρημα μέσης τιμής υπάρχει τουλάχιστον ένα ξ στο διάστημα (α,β) τέτοιο ώστε

F΄(ξ)=(F(β)-F(α))/(β-α) -> f(ξ)=S(α,β)f(t)dt/(β-α)

Civilara · 10-05-09

Έστω συνάρτηση f κυρτή στο R με συνεχή παράγωγο και συνάρτηση g ορισμένη στο R με g(x)>0 για κάθε x στο R. Υπάρχουν 0<α<β τέτοια ώστε:

i) f΄(x)=ln[g(x)]+(e^x) για κάθε x ανήκει R

ii) S(α,x)f(t)dt>=f(x-α) για κάθε x ανήκει στο R

iii) f(β)=f΄(0) και f(0)=0

(α) να αποδείξετε ότι υπάρχει μοναδικό ξ στο R τέτοιο ώστε [g(ξ)]^2=e^(-2*(e^ξ)) για το οποίο ισχύει 0<g(ξ)<1

S(α,x)f(t)dt : ορισμένο ολοκλήρωμα της f με κάτω όριο ολοκλήρωσης το α και πάνω όριο το x

(β) να αποδείξετε ότι η f παρουσιάζει ολικό ελάχιστο στο σημείο (ξ, f(ξ)) το οποίο είναι και το μοναδικό ακρότατο της Cf.

(γ) να αποδείξετε ότι η Cg δεν μπορεί να έχει κατακόρυφες ασύμπτωτες

(δ) Αν η f είναι δύο φορές παραγωγίσιμη στο γ ανήκει R, η g είναι παραγωγίσιμη στο γ και ισχύει γ=lnf΄΄(γ) τότε η Cg έχει οριζόντια εφαπτομένη στο (γ, g(γ))

ledzeppelinick · 10-05-09

α) λυνοντας ως προς g(x) στην δεδομενη σχεση i) έχουμε g(x)=e^(f'(x)-e^x) και το αντικαθιστουμε στην εξισωση που θελουμε να αποδειξουμε και μετα απο πραξειες προκυπτει οτι για να αποδειχτει το ζητουμενο αρκει να δειξουμε οτι f'(ξ)=0 πραγμα που αποδεικνυεται νομιζω με Rolle στο (α,β) για την f . και ειναι μοναδικο αφου f κυρτη άρα f' γνησιως αυξουσα.
β)για χ>=ξ, f'(x)>=f'(ξ) , f(χ)>=0 οπου ξ το ξ του προηγ ερωτηματος και f' γν αυξουσα. για χ=<ξ, f'(χ)=<f'(ξ), f'(χ)=<0. η f γν φθινουσα στο (-οο,0) και γν αυξουσα στο (0,+οο) άρα παρουσιαζει ολικο ελαχιστο στο ξ το f(ξ) το οποιο ειναι μοναδικο αφου η f ειναι ορισμενη στο R ειναι παραγωγισιμη και το μοναδικο σημειο οπου f'(χ)=0 είναι το (ξ,f(ξ))
γ) η g ειναι ορισμενη στο R οποτε δεν παρουσιαζει κατακορυφες ασυμπτωτες
δ)αρκει ν.δ.ο. g'(γ)=0. απο τη δοσμενη σχεση i) λύνουμε ως προς g g(x)=e^(f'(x)-e^x) και αφου η g παραγωγισιμη στο γ έχουμε g'(γ)=(f''(γ)-e^γ)*e^(f'(γ)-e^γ) άρα για να ισχυει g'(γ)=0 αρκει f''(γ)=e^γ, lnf''(γ)=γ το οποιο ισχυει
-----------------------------------------
με συγχωρειτε για τα λαθη και για τις ελλειψεις απλα εκανα μια προσπαθεια να την προσεγγισω! θα ηθελα να δω και την λυση mr. geoste για να διορθοθω!! αν δεν θελετε να την γραψετε εδω στειλτε την μου στο προφιλ μου! Ευχαριστω εκ των προτερων! :thanks:

Civilara · 10-05-09

Έκανα μία διόρθωση στην εκφώνηση. Είχα δώσει ένα δεδομένο που δεν χρειαζόταν. Κατά τα άλλα είναι σωστή.

Όσον αφορά την απάντησή σου στο γ) δεν είναι σωστή. Για παράδειγμα θεώρησε την συνάρτηση

f(x)=1/x, x διάφορο 0
f(x)=0 , x=0

Η f είναι ορισμένη στο R αλλά παρουσιάζει στο x0=0 κατακόρυφη ασύμπτωτη (άξονας y΄y)

ledzeppelinick · 10-05-09

η 1/χ δεν ειναι ορισμενη στο (-οο,0)U(ο,+οο)? και στο 0 οπου δεν οριζεται παρουσιαζει ασυμπτωτη.. η στο 0 που δεν ειναι συνεχης.. άρα για την g δεν μπορουμε να παραουμε το οριο της να τεινει σε ενα ανοιχτο σημειο που δεν οριζεται και να βγει +-οο.. που κανω λαθος?? :'(

Civilara · 10-05-09

Μία συνάρτηση μπορεί να έχει κατακόρυφη ασύμπτωτη σε σημείο που ανήκει στο πεδίο ορισμού της. ΔΕΝ σημαίνει ότι αν ορίζεται σε ένα σημείο τότε δεν έχει κατακόρυφη ασύμπτωτη.

Αν μία συνάρτηση είναι ΣΥΝΕΧΗΣ (όχι απλά ορισμένη) σε ένα σημείο x0 τότε ΔΕΝ έχει κατατκόρυφη ασύμπτωτη στο x0.

m3Lt3D · 10-05-09

Αρχική Δημοσίευση από giannis:
Μια απόδειξη για το :αν $f(x)>0$ και $int_{a}^{b}f(x)dx=0$ τότε $a=b$

αν θεωρήσουμε $F(x)=int_{a}^{x}f(t)dt$ τότε

$F^{prime}(x)=f(x)>0$ άρα $F$ είναι γν. αύξουσα άρα και 1-1

άρα $int_{a}^{b}f(x)dx=0 Leftrightarrow F(a)=F(b) Leftrightarrow a=b$

μια διαφορετικη αποδειξη:
εστω α<β. αφου f(x)>0=> $\int_{a}^{b}f(x)dx>0$ . ατοπο
ομοια για β<α.
αρα α=β

ledzeppelinick · 10-05-09

ναι καταλαβα! ευχαριστω! :thanks:άρα λυνουμε την εξισωση στο α ερωτημα ως προς g και αποδεικνυουμε οτι δεν απεριζεται σε κανενα σημειο το οριο της? τι κανουμε? η λεμε οτι ειναι συνεχης επειδη ειναι ιση με ριζαe^(-2*(e^χ))?? ευχαριστω εκ των προτερων!!

Civilara · 10-05-09

Αρχική Δημοσίευση από ledzeppelinick:
ναι καταλαβα! ευχαριστω! :thanks:άρα λυνουμε την εξισωση στο α ερωτημα ως προς g και αποδεικνυουμε οτι δεν απεριζεται σε κανενα σημειο το οριο της? τι κανουμε? η λεμε οτι ειναι συνεχης επειδη ειναι ιση με ριζαe^(-2*(e^χ))?? ευχαριστω εκ των προτερων!!

Λύνουμε ως προς g και προκύπτει g(x)=e^(f΄(x)-(e^x)). Άρα g συνεχής στο R, αφού f΄ συνεχής στο R. Άρα δεν έχει κατακόρυφες ασύμπτωτες.

ledzeppelinick · 10-05-09

αααα... χτες που την ελυσα νομιζω δεν ελεγε οτι η f εχει συνεχη παραγωγο.. Ευχαριστω παντως!! πολυ ωραια ασκηση!!

Civilara · 10-05-09

έχεις δίκιο, είχα ξεχάσει να το γράψω. Sorry

ledzeppelinick · 10-05-09

να ρωτησω και κατι ακομα. στο α ερωτημα απ οσο το εκανα κανουμε Θ. Fermat για την h(x)=S(α,x)f(t)dt-f(x-α) και ο μονος τροπος να παρουμε οτι f(a)=f(b) είναι το h'(α)=0.. αλλα κανει το f(0)=0 έτσι ωστε να εχουμε ορισμο ελεαχιστου δηλαδη h(x)>=h(a)?? ελπιζω να γινομαι κατανοητος..:s
-----------------------------------------
οκ το αλλαξατε στα δεδομενα!! ευχαριστω!! και συγγνωμη για το πρηξιμο

odyracer18 · 11-05-09

Αρχική Δημοσίευση από lostG:
Ξαναδές την λίγο γιατί είναι λάθος.Αυτό που λες δεν είναι σωστό δηλαδή,
f(z)=f(α+βi)=f(α)+f(βi)

αφού , απο υπόδεση ισχύει ότι f(z1+z2)=f(z1)+f(z2)
οπότε, για z1=α και z2=βi γίνεται
f(z)=f(α+βi)=f(α)+f(βi)

σορρυ,αλλά το είχα γράψει λίγο σύντομα και δεν τα αιτιολογούσα όλα

Metal-Militiaman · 12-05-09

Ρε παιδιά μήπως ξέρετε που μπορώ να βρω τις απαντήσεις, ειδικά αν ξέρεται ποιος είναι ο τρόπος λύσης του 3ου θέματος(γ ερώτημα)
(και 4ο δεν θα με χαλούσε,αν μου στέλνατε τις απαντήσεις)
https://www.ypepth.gr/themata/them_mat_kat_c_hmer_epan_0705.pdf

νομίζω ότι κάτι δεν μου καλλάει στο τρίτο ερώτημα του 3ου θέματος

Συλλογή ασκήσεων και τεστ στα Μαθηματικά Προσανατολισμού

Πολύ δραστήριο μέλος

Πολύ δραστήριο μέλος

Εκκολαπτόμενο μέλος

Πολύ δραστήριο μέλος

Εκκολαπτόμενο μέλος

Περιβόητο μέλος

Περιβόητο μέλος

Περιβόητο μέλος

Πολύ δραστήριο μέλος

Περιβόητο μέλος

Πολύ δραστήριο μέλος

Περιβόητο μέλος

Πολύ δραστήριο μέλος

Πολύ δραστήριο μέλος

Περιβόητο μέλος

Πολύ δραστήριο μέλος

Περιβόητο μέλος

Πολύ δραστήριο μέλος

Νεοφερμένος

Νεοφερμένος