Συλλογή ασκήσεων και τεστ στα Μαθηματικά Προσανατολισμού

rebel · 9 Μαρτίου 2011

Κι εγώ με Θ.Μ.Τ. το σκέφτηκα για την $f(x)=x^{\frac{x+1}{x}} \ \exists \xi(x)=\xi \in (x,x+1):f'(\xi)=f(x+1)-f(x)$ .

Είναι $f'(\xi)=\xi^{\frac{\xi+1}{\xi}}\cdot\frac{\xi+1-\ln \xi}{\xi^2}=\frac{\xi^\frac{\xi+1}{\xi}}{\xi}\cdot \frac{\xi+1-\ln\xi}{\xi}=\xi^\frac{1}{\xi}\cdot \left(1+\frac{1}{\xi}-\frac{\ln \xi}{\xi}\right)$

Όμως $\lim_{\xi \to +\infty} \xi^\frac{1}{\xi}=\lim_{\xi \to +\infty} e^{\frac{\ln \xi}{\xi}}=1$ αφού
$\lim_{\xi \to +\infty} \frac{\ln \xi}{\xi}=0$ από De L'Hospital οπότε $\lim_{\xi \to +\infty}f'(\xi)=1$

Επεξεργασία:
Τελικά $\color{red}{\lim_{x \to +\infty}\left[f(x+1)-f(x)\right]=\lim_{x \to +\infty}f'(\xi(x))=1}$
αφού $\color{red}{\lim_{x \to +\infty}\xi(x)= +\infty}$ και αποδείξαμε πάνω ότι $\color{red}{\lim_{\xi \to +\infty}f'(\xi)=1}$ . Χάνω κάπου;

Rempeskes · 08-03-11

Το Spoiler δεν είναι δικαιολογημένο.
Δεν μας εγγυάται κανείς πως
το όριο του περιορισμού ξ=ξ(χ) όταν χ τείνει στο άπειρο, θα είναι ίσο
με το όριο όταν το x τείνει στο άπειρο.

Metal-Militiaman · 09-03-11

για ένα διάστημα [α,β] όπου ισχύουν οι προυποθέσεις του Θ.Μ.Τ το ξ= α+θ(β-α) , 0<θ<1 με λίγα λόγια το ξ εξαρτάται τόσο από τα άκρα α,β όσο και από την παράμετρο θ.
Στην περίπτωση [x,x+1] είναι ξ(χ,θ)=χ+θ, 0<θ<1 οπότε ξ->+ΟΟ όταν χ->+ΟΟ.
Επομένως η απάντηση του sty_geia είναι σωστή.
Ένα παρόμοιο παράδειγμα
$\lim_{x\rightarrow +\propto }x({e}^{\frac{1}{x+1}}-{e}^{\frac{1}{x}})$

vassilis498 · 09-03-11

καλά με δέρνει η κωλοφαρδία, τέτοιο όριο βάλανε φροντιστήριο στο διαγώνισμα στο διαφορικό λογισμό τέταρτο θέμα, θα χανα 5-10 μόρια

Chris1993 · 09-03-11

Ορίστε και απο μένα μια άσκηση που είναι καλή νομίζω!

Άν $f$ παραγωγίσιμη στο $[\alpha ,\beta]$
και
$f(x)=(x-\alpha )(x-\beta )f'(x)$
Να δείξετε ότι η $f$ είναι σταθερή στο $[\alpha ,\beta]$

Rempeskes · 09-03-11

Αρχική Δημοσίευση από Metal-Militiaman:
για ένα διάστημα [α,β] όπου ισχύουν οι προυποθέσεις του Θ.Μ.Τ το ξ= α+θ(β-α) , 0<θ<1 με λίγα λόγια το ξ εξαρτάται τόσο από τα άκρα α,β όσο και από την παράμετρο θ.

Mόνο που η παράμετρος θ δεν είναι μονοσήμαντη συνάρτηση του ξ, καθώς
συχνά το ξ δεν είναι μοναδικό.
Mα και μοναδικό να είναι, δηλαδή ξ=ξ(χ),
κοντά σε σημεία όπου f'=0, μπορεί το liminfξ και το limsupξ να είναι διαφορετικά,
όπως μπορεί να πιστοποιήσει οποιοσδηποτε έχει δει
το πισι του να κρασάρει
στην εφαρμογή μιας Newton-Raphson.

vassilis498 · 16-03-11

Αρχική Δημοσίευση από Chris1993:
Ορίστε και απο μένα μια άσκηση που είναι καλή νομίζω!

Άν $f$ παραγωγίσιμη στο $[\alpha ,\beta]$
και
$f(x)=(x-\alpha )(x-\beta )f'(x)$
Να δείξετε ότι η $f$ είναι σταθερή στο $[\alpha ,\beta]$

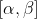
μη μείνει άλυτη

$f(x)=(x-\alpha )(x-\beta )f'(x)$

f(a)=f(b)=0

f ορισμένη και παραγωγίσιμη σε κλειστό διάστημα, άρα θα έχω χ1,χ2 στο (α,β) τέτοια ώστε f(x)>=f(x1), f(x)=<f(x2)
εάν α,β βρίσκονται στο εσωτερικό του διαστήματος [α,β] τότε από Fermat έχω f'(x1)=f'(x2)=0
άρα για χ=x1, χ=x2 στη σχέση που μου δίνεται έχω f(x1)=f(x2)=0

επίσης αν πάλι κάποιο από τα χ1,χ2 ( ή και τα 2) είναι άκρο του διαστήματος, τότε πάλι θα κάνει 0. ( f(a)=f(b)=0 )

άρα σε κάθε περίπτωση έχω 0=<f(x)=<0
f(x)=0 σταθερή

manos66 · 17-03-11

AΣΚΗΣΗ
Έστω η συνάρτηση f : R-->R* και η συνάρτηση g, με $g(x)=\int_{2011}^{x}f(t)dt - \int_{x}^{2013}f(t)dt, x\epsilon R$ .
Ισχύει επίσης $\int_{2011}^{2013}tf(t)dt = 2012$ και $\int_{2011}^{2013}f(t)dt = 1$ .
α. Ν.δ.ο. υπάρχει ένα τουλάχιστον $\xi\epsilon (2011,2013)$ , τέτοιο ώστε ξf(ξ)=1006.
β. Ν.δ.ο. f (x) > 0, για κάθε $x\epsilon R$ .
γ. Να μελετηθεί η g ως προς τη μονοτονία.
δ. Ν.δ.ο η g έχει ακριβώς μία ρίζα στο διάστημα (2011 , 2013).
ε. Να υπολογιστεί το ολοκλήρωμα $\int_{2011}^{2013}g(t)dt$ .

vassilis498 · 18-03-11

ξέρουμε αν f είναι συνεχής;

rebel · 18-03-11

Nομίζω ότι παρά την παράλειψη στην εκφώνηση, εξυπακούεται ότι η f ειναι συνεχής. Αλλιώς δεν θα είχε νόημα το $\int_a^x \! f(t) \, \mathrm{d}t$ . Προχώρα άφοβα!

13diagoras · 18-03-11

Βαζω μια ασκηση την οποια θεωρω αρκετα ενδιαφερουσα:

Αν η εξισωση αχ²+βχ+γ=0 με α,β,γ,ανηκουν στους πραγματικους και β²

αγ εχει ριζες κ,λ,
(α)Να δειξετε οτι δεν ειναι πραγματικες οι ριζες
(β)ο μιγας w=κ/λ +λ/κ ειναι πραγματικος και ισχυει w<1
(γ)η εξισωση (αχ³+βχ²+γχ)e^χ=α εχει ακριβως μια πραγματικη ριζα

Καλη λυση!!

Dias · 19-03-11

Αρχική Δημοσίευση από 13diagoras:
Αν η εξισωση αχ²+βχ+γ=0 με α,β,γ,ανηκουν στους πραγματικους .....

Αν οι α, β, γ ήταν θετικοί, είναι πολύ απλή. Αν δεν είναι, Δ.Ξ./Δ.Α.

Leo 93 · 19-03-11

Αρχική Δημοσίευση από manos66:
AΣΚΗΣΗ
Έστω η συνάρτηση f : R-->R* και η συνάρτηση g, με $g(x)=\int_{2011}^{x}f(t)dt - \int_{x}^{2013}f(t)dt, x\epsilon R$ .
Ισχύει επίσης $\int_{2011}^{2013}tf(t)dt = 2012$ και $\int_{2011}^{2013}f(t)dt = 1$ .
α. Ν.δ.ο. υπάρχει ένα τουλάχιστον $\xi\epsilon (2011,2013)$ , τέτοιο ώστε ξf(ξ)=1006.
β. Ν.δ.ο. f (x) > 0, για κάθε $x\epsilon R$ .
γ. Να μελετηθεί η g ως προς τη μονοτονία.
δ. Ν.δ.ο η g έχει ακριβώς μία ρίζα στο διάστημα (2011 , 2013).
ε. Να υπολογιστεί το ολοκλήρωμα $\int_{2011}^{2013}g(t)dt$ .

Μια προσπάθεια:

α. Mε Θ.Μ.Τ. για την αρχική της $xf(x)$ στο $[2011,2013]$ έχουμε ότι υπάρχει $\xi \in (2011,2013):\xi f(\xi )=\frac{\int_{2011}^{2013}f(x)dx}{2013-2011}=\frac{2012}{2}=1006$ .

β. ...Η f διατηρεί πρόσημο.
Είναι $\xi f(\xi )=1006\Rightarrow f(\xi )=\frac{1006}{\xi }>0$ .
Άρα $f(x)>0$ για κάθε $x\epsilon R$

γ. $g'(x)=\left( \int_{2011}^{x}f(t)dt-\int_{x}^{2013}f(t)dt\right)'=2f(x)>0$ για κάθε $x\epsilon R$ άρα g γνησίωε αύξουσα,

δ. $g(2011)=-\int_{2011}^{2013}f(t)dt<0$ αφού $f(x)>0$ .
Για τον ίδιο λόγο είναι $g(2013)>0$ .
Άρα (θ. Bolzano) η $g(x)=0$ έχει μία τουλάχιστον ρίζα στο $[2011,2013]$ , που είναι τελικά, λόγω μονοτονίας. μοναδική.

ε.To ζητούμενο ολοκλήρωμα ισούται με $\int_{2011}^{2013}\left( \int_{2011}^{x}f(t)dt\right)dx-\int_{2011}^{2013}\left( \int_{x}^{2013}f(t)dt\right)dx=\int_{2011}^{2013}(x)'\left( \int_{2011}^{x}f(t)dt\right)dx-\int_{2011}^{2013}(x)'\left( \int_{x}^{2013}f(t)dt\right)dx=\left[ x\int_{2011}^{x}f(t)dt\right]{}_{2011}{}^{2013}-\int_{2011}^{2013}xf(x)dx-\left[ x\int_{2011}^{x}f(t)dt\right]{}_{2011}{}^{2013}+\int_{2011}^{2013}xf(x)dx=0$

To (δ) δε χρειάστηκε για το (ε)...

vassilis498 · 19-03-11

(γ)η εξισωση (αχ³+βχ²+γχ)e^χ=α εχει ακριβως μια πραγματικη ριζα

μιλάμε για το ίδιο α;

Leo 93 · 19-03-11

Αρχική Δημοσίευση από Leo 93:
Μια προσπάθεια:

α. Mε Θ.Μ.Τ. για την αρχική της $xf(x)$ στο $[2011,2013]$ έχουμε ότι υπάρχει $\xi \in (2011,2013):\xi f(\xi )=\frac{\int_{2011}^{2013}f(x)dx}{2013-2011}=\frac{2012}{2}=1006$ .

β. ...Η f διατηρεί πρόσημο.
Είναι $\xi f(\xi )=1006\Rightarrow f(\xi )=\frac{1006}{\xi }>0$ .
Άρα $f(x)>0$ για κάθε $x\epsilon R$

γ. $g'(x)=\left( \int_{2011}^{x}f(t)dt-\int_{x}^{2013}f(t)dt\right)'=2f(x)>0$ για κάθε $x\epsilon R$ άρα g γνησίωε αύξουσα,

δ. $g(2011)=-\int_{2011}^{2013}f(t)dt<0$ αφού $f(x)>0$ .
Για τον ίδιο λόγο είναι $g(2013)>0$ .
Άρα (θ. Bolzano) η $g(x)=0$ έχει μία τουλάχιστον ρίζα στο $[2011,2013]$ , που είναι τελικά, λόγω μονοτονίας. μοναδική.

ε.To ζητούμενο ολοκλήρωμα ισούται με $\int_{2011}^{2013}\left( \int_{2011}^{x}f(t)dt\right)dx-\int_{2011}^{2013}\left( \int_{x}^{2013}f(t)dt\right)dx=\int_{2011}^{2013}(x)'\left( \int_{2011}^{x}f(t)dt\right)dx-\int_{2011}^{2013}(x)'\left( \int_{x}^{2013}f(t)dt\right)dx=\left[ x\int_{2011}^{x}f(t)dt\right]{}_{2011}{}^{2013}-\int_{2011}^{2013}xf(x)dx-\left[ x\int_{2011}^{x}f(t)dt\right]{}_{2011}{}^{2013}+\int_{2011}^{2013}xf(x)dx=0$

To (δ) δε χρειάστηκε για το (ε)...

Διόρθωση τυπογραφικού λάθους στο (ε):

To $\left[ x\int_{2011}^{x}f(t)dt\right]{}_{2011}{}^{2013}$ να αντικατασταθεί με $\left[ x\int_{x}^{2013}f(t)dt\right]{}_{2011}{}^{2013}$ και το αποτέλεσμα είναι 2.

13diagoras · 19 Μαρτίου 2011

Δια δεν σε επιασα με τα Δ.Ξ/Δ.Α. ,δεν ειναι θετικοι οι αριθμοι γιατι απλα δεν το λεει.
Βασιλη,ναι.Eιναι το ιδιο το α!

Υ.Γ.(1) το α! δεν ειναι παραγοντικο

Y.Γ.(2) Πως γινεται η πoλλαπλη παραθεση?

vassilis498 · 19-03-11

Y.Γ.(2) Πως γινεται η πoλλαπλη παραθεση?

πάτα το σε 2-3 post και μετά πάτα απάντηση και θα καταλάβεις

Dias · 19-03-11

Αρχική Δημοσίευση από 13diagoras:
Δια δεν σε επιασα με τα Δ.Ξ/Δ.Α. ,δεν ειναι θετικοι οι αριθμοι γιατι απλα δεν το λεει.

Δίκιο έχεις, βιάστηκα. Γίνεται και χωρίς να είναι θετικοί. Μόλις όμως τελείωσα μια γενική-γενική επανάληψη στην ηλεκτρολογία και δεν έχω άλλη ενέργεια για ασκήσεις.

13diagoras · 20-03-11

Βαζω μια ασκηση την οποια θεωρω αρκετα ενδιαφερουσα:

Αν η εξισωση αχ²+βχ+γ=0 με α,β,γ,ανηκουν στους πραγματικους και β²αγ εχει ριζες κ,λ,
(α)Να δειξετε οτι δεν ειναι πραγματικες οι ριζες
(β)ο μιγας w=κ/λ +λ/κ ειναι πραγματικος και ισχυει w<1
(γ)η εξισωση (αχ³+βχ²+γχ)e^χ=α εχει ακριβως μια πραγματικη ριζα

Την προσπαθησε κανεις,να βαλω λυση? :bounce:

Αρχική Δημοσίευση από Dias:
Μόλις όμως τελείωσα μια γενική-γενική επανάληψη στην ηλεκτρολογία και δεν έχω άλλη ενέργεια για ασκήσεις.

Αν κανεις μια μερα να συνελθεις απο την ηλεκτρολογια,τοτε
νοιωθω μεγαλη ικανοποιηση απο την επιλογη μου να παω τεχνο2

vassilis498 · 21 Μαρτίου 2011

Βαζω μια ασκηση την οποια θεωρω αρκετα ενδιαφερουσα:

Αν η εξισωση αχ²+βχ+γ=0 με α,β,γ,ανηκουν στους πραγματικους και β²αγ εχει ριζες κ,λ,
(α)Να δειξετε οτι δεν ειναι πραγματικες οι ριζες
(β)ο μιγας w=κ/λ +λ/κ ειναι πραγματικος και ισχυει w<1

^

a) αχ²+βχ+γ=0

$\Delta ={\beta }^{2}-4\alpha \gamma <{\beta }^{2}-3\alpha \gamma <0$
άρα οι όποιες ρίζες είναι μιγαδικές

b)κ,λ μιγαδικές ρίζες της εξίσωσης, άρα έχω $\kappa =\bar{\lambda }$

$w=\frac{\kappa }{\lambda }+\frac{\lambda }{\kappa }=\frac{\bar{\lambda }}{\lambda }+\frac{\lambda}{\bar{\lambda }}=\frac{{\bar{\lambda }}^{2}+{\lambda }^{2}}{{\left|\lambda \right|}^{2}}=\frac{2Re({\lambda }^{2})}{{\left|\lambda \right|}^{2}}$

$\lambda =\frac{-\beta +\sqrt{4\alpha \gamma -{\beta }^{2}}i}{2\alpha }$

${\lambda }^{2}=\frac{2{\beta }^{2}-4\alpha \gamma }{4{a}^{2}}-\frac{2\beta \sqrt{4\alpha \gamma -{\beta }^{2}}i}{4{\alpha }^{2}}$

$2Re({\lambda }^{2})=\frac{{\beta }^{2}-2\alpha \gamma }{{\alpha }^{2}}$

${\left|\lambda \right|}^{2}=\frac{{\beta }^{2}}{4{\alpha }^{2}}+\frac{4\alpha \gamma -{\beta }^{2}}{4{\alpha }^{2}}=\frac{\alpha \gamma }{{\alpha }^{2}}$

$<3$ \alpha \gamma \Leftrightarrow {\beta }^{2}-2\alpha \gamma <\alpha \gamma \Leftrightarrow \frac{{\beta }^{2}-2\alpha \gamma }{{a}^{2}}<\frac{\alpha \gamma }{{a}^{2}}\Leftrightarrow 2Re({\lambda }^{2})<{\left|\lambda \right|}^{2}\Leftrightarrow w<1" />

το (γ) το παλεύω..

edit: (γ)

έστω $f(x)={e}^{x}(\alpha {x}^{3}+\beta {x}^{2}+\gamma x), x\epsilon R$
για α<0:
$f(0)=0$

$\lim_{x->+oo}f(x)=-oo$

επίσης f παραγωγήσιμη ως πράξεις παραγωγίσιμων.
από Θ.Ε.Τ έχω ένα τουλάχιστον Χο στο (0,+οο) τέτοιο ώστε f(Xo)=a
αντίστοιχα για α>0

άρα η εξίσωση έχει τουλάχιστον μια ρίζα.

${e}^{x}(\alpha {x}^{3}+\beta {x}^{2}+\gamma x)=a\Leftrightarrow x{e}^{x}(\alpha {x}^{2}+\beta x+\gamma )=\alpha$

για α>0:
$x<0\Leftrightarrow x{e}^{x}(\alpha {x}^{2}+\beta x+\gamma )<0$ (το τριώνυμο είναι πάντα θετικό λόγω αρνητικής διακρίνουσας)
άρα δεν μπορώ να έχω ρίζα για χ<0 αφού το πρώτο μέλος βγαίνει αρνητικό ενώ α>0
για χ>0 λοιπόν
έστω ότι έχω 2 ρίζες χ1,χ2. Τότε από rolle στο (χ1,χ2) έχω χ3 τέτοιο ώστε f'(x3)=0

$f'(x)={e}^{x}(3\alpha {x}^{2}+2\beta x+\gamma )+x{e}^{x}(\alpha {x}^{2}+\beta x+\gamma )>0$ (τα πολυώνυμα θετικά λόγω διακρίνουσας.)
άτοπο. άρα η ρίζα είναι μοναδική.

για α<0.
$x<0\Leftrightarrow x{e}^{x}(\alpha {x}^{2}+\beta x+\gamma )>0$
άρα δεν έχω ρίζα στα αρνητικά, εφόσον το πρώτο μέλος βγαίνει ετερώσημο του α.
για χ>0 λοιπόν.
πάλι έστω ότι έχω 2 ρίζες χ4,χ5 αντίστοιχα άρα από rolle στο (χ4,χ5) θα έχω χ6 στο διάστημα αυτό τέτοιο ώστε f'(x6)=0
$f'(x)={e}^{x}(3\alpha {x}^{2}+2\beta x+\gamma )+x{e}^{x}(\alpha {x}^{2}+\beta x+\gamma )<0$ (πολυώνυμα αρνητικά τώρα λόγω αρνητικής διακρίνουσας, και αρνητικού α)
άτοπο. άρα η λύση είναι μοναδική

και σωστό να ναι, είμαι σίγουρος ότι βγαίνει και πιο γρήγορα αλλά δε βαριέσαι

Συλλογή ασκήσεων και τεστ στα Μαθηματικά Προσανατολισμού

Πολύ δραστήριο μέλος

Επιφανές μέλος

Νεοφερμένος

Διακεκριμένο μέλος

Περιβόητο μέλος

Επιφανές μέλος

Διακεκριμένο μέλος

Εκκολαπτόμενο μέλος

Διακεκριμένο μέλος

Πολύ δραστήριο μέλος

Δραστήριο μέλος

Επιφανές μέλος

Εκκολαπτόμενο μέλος

Διακεκριμένο μέλος

Εκκολαπτόμενο μέλος

Δραστήριο μέλος

Διακεκριμένο μέλος

Επιφανές μέλος

Δραστήριο μέλος

Διακεκριμένο μέλος