Βοήθεια/Aπορίες στα Μαθηματικά Προσανατολισμού

φρι · 04-02-13

Αρχική Δημοσίευση από JKaradakov:
Έστω! Πάρε ξ1 και ξ2. Το θέμα μου είναι ότι μπορεί να είναι αλλά μπορεί και να μην είναι ίσα. Αυτό ρωτάω.

Αχα . Μπορεί τελικά να αποδείξεις ότι ξ1=ξ2 αλλά δε σε νοιαζει

Civilara · 4 Φεβρουαρίου 2013

Αρχική Δημοσίευση από JKaradakov:
Μια ερώτηση. Έχω μια συνάρτηση f δις παραγωγίσημη.
Κάνω Θ.Rolle στην f και βγάζω ξ που ανείκη στο (α,β): f'(ξ)=0
Κάνω Θ.Rolle στην f' και βγάζω ξ που ανείκη στο (α,β): f''(ξ)=0
Αυτά τα δύο ξ δεν είναι το ίδιο, έτσι;
Μπορεί να είναι αλλά μπορεί και να μην είναι.

Δεν είναι απαραίτητο να είναι ίσα αλλά ούτε και αποκλείεται. Για παράδειγμα η συνάρτηση f(x)=ημx+συνx, x ανήκει R. Η f είναι 2 φορές παραγωγίσιμη στο R με παρσγώγους:

f΄(x)=συνx-ημx
f΄΄(x)=-ημx-συνx=-f(x)

Λύνουμε τις εξισώσεις f(x)=0, f΄(x)=0, f΄΄(x)=0. (Οι εξισώσεις f(x)=0 και f΄΄(x)=0 είναι ισοδύναμες αφού f΄΄(x)=-f(x))

f΄΄(x)=0 <=> f(x)=0 <=> ημx+συνx=0 <=> ημx=-συνx <=> εφx=-1 <=> εφx=εφ(-π/4) <=> x=κπ-(π/4) όπου κ ανήκει Ζ
f΄(x)=0 <=> συνx-ημx=0 <=> ημx=συνx <=> εφx=1 <=> εφx=εφ(π/4) <=> x=λπ+(π/4) όπου λ ανήκει Ζ

Για να έχουν κοινές ρίζες οι εξισώσεις f΄(x)=0 και f΄΄(x)=0 πρέπει να υπάρχουν ακέραιοι κ,λ τέτοιοι ώστε:
κπ-(π/4)=λπ+(π/4) <=> κπ=λπ+(π/2) <=> κ=λ+(1/2) που είναι άτοπο αφού για κάθε λ ανήκει Ζ ο [λ+(1/2)] δεν είναι ακέραιος.

Για κ ανήκει Ζ έχουμε:
ημ(κπ+φ)=ημ(κπ)συνφ+συν(κπ)ημφ=0*συνφ+((-1)^|κ|)ημφ=[(-1)^|κ|]ημφ
συν(κπ+φ)=συν(κπ)συνφ-ημ(κπ)ημφ=((-1)^|κ|)συνφ-0*ημφ=[(-1)^|κ|]συνφ

Άρα
ημ(κπ-(π/4))=[(-1)^|κ|]ημ(-π/4)=-(SQRT(2)/2)*[(-1)^|κ|]
συν(κπ-(π/4))=[(-1)^|κ|]συν(-π/4)=(SQRT(2)/2)*[(-1)^|κ|]

ημ(κπ+(π/4))=[(-1)^|κ|]ημ(π/4)=(SQRT(2)/2)*[(-1)^|κ|]
συν(κπ+(π/4))=[(-1)^|κ|]συν(π/4)=(SQRT(2)/2)*[(-1)^|κ|]

f΄(κπ-(π/4))=(SQRT(2)/2)*[(-1)^|κ|]+(SQRT(2)/2)*[(-1)^|κ|]=SQRT(2)*[(-1)^|κ|] διάφορο 0
f΄΄(κπ-(π/4))=(SQRT(2)/2)*[(-1)^|κ|]-(SQRT(2)/2)*[(-1)^|κ|]=0

f΄(κπ+(π/4))=(SQRT(2)/2)*[(-1)^|κ|]-(SQRT(2)/2)*[(-1)^|κ|]=0
f΄΄(κπ+(π/4))=-(SQRT(2)/2)*[(-1)^|κ|]-(SQRT(2)/2)*[(-1)^|κ|]=-SQRT(2)*[(-1)^|κ|] διάφορο 0

Οι συναρτήσεις f, f΄ και f΄΄ είναι περιοδικές με περίοδο Τ=2π. Αυτό σημαίνει ότι για κάθε κ ανήκει Ζ* και για κάθε x ανήκει R ισχύουν:

f(x+2κπ)=f(x)
f΄(x+2κπ)=f΄(x)
f΄΄(x+2κπ)=f΄΄(x)

Η f είναι συνεχής στο διάστημα [x0+2κπ, x0+2(κ+1)π], παραγωγίσιμη στο (x0+2κπ, x0+2(κ+1)π) και ισχύει f(x0+2(κ+1)π)=f(x0+2κπ)=f(x0) για κάθε κ ανήκει Z και όπου x0 ανήκει R. Επομένως σύμφωνα με το θεώρημα Rolle υπάρχει τουλάχιστον ένα ξ1 στο διάστημα (x0+2κπ, x0+2(κ+1)π) τέτοιο ώστε f΄(ξ1)=0.

Η f΄ είναι συνεχής στο διάστημα [x0+2κπ, x0+2(κ+1)π], παραγωγίσιμη στο (x0+2κπ, x0+2(κ+1)π) και ισχύει f΄(x0+2(κ+1)π)=f΄(x0+2κπ)=f΄(x0) για κάθε κ ανήκει Z και όπου x0 ανήκει R. Επομένως σύμφωνα με το θεώρημα Rolle υπάρχει τουλάχιστον ένα ξ2 στο διάστημα (x0+2κπ, x0+2(κ+1)π) τέτοιο ώστε f΄΄(ξ2)=0.

Όμως επειδή οι εξισώσεις f΄(x)=0 και f΄΄(x)=0 δεν έχουν καμία κοινή ρίζα τότε ισχύει ξ1 διάφορο ξ2.

Mercury · 04-02-13

Να λύσετε την εξίσωση:
${z}^{3}-2i{z}^{2}=6i-3z$
Την έχω φτάσει με το παρακάτω σημείο και μετά κολλάω...

${z}^{3}-2i{z}^{2}=6i-3z\Rightarrow {z}^{3}-3z=6i+2i{z}^{2}\Rightarrow z({z}^{2}-3)=2i(3+{z}^{2})\Rightarrow \frac{z({z}^{2}-3)}{({z}^{2}+3)}=2i$

exc · 4 Φεβρουαρίου 2013

Αρχική Δημοσίευση από Mercury:
Να λύσετε την εξίσωση:
${z}^{3}-2i{z}^{2}=6i-3z$
Την έχω φτάσει με το παρακάτω σημείο και μετά κολλάω...

${z}^{3}-2i{z}^{2}=6i-3z\Rightarrow {z}^{3}-3z=6i+2i{z}^{2}\Rightarrow z({z}^{2}-3)=2i(3+{z}^{2})\Rightarrow \frac{z({z}^{2}-3)}{({z}^{2}+3)}=2i$

Αριστερά (στα fm

) βγάλε κοινό παράγοντα το z² και δεξιά το -3.
Φέρε τα όλα στο ένα μέλος και κάνε παραγοντοποίηση.
Ρίζες: z=±sqrt(3)i, z=2i.

Have fun και καλή επιτυχία.

Dias · 04-02-13

Αρχική Δημοσίευση από Mercury:
Να λύσετε την εξίσωση:
${z}^{3}-2i{z}^{2}=6i-3z$

=> z³ - 2iz² + 3z - 6i = 0 => z²(z - 2i) + 3(z - 2i) = 0 => (z - 2i)(z² +3) = 0 =>
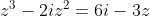
z = 2i , z = +i√3̅ , z = -i√3̅ .

Mercury · 04-02-13

Αρχική Δημοσίευση από exc:
Αριστερά (στα fm ) βγάλε κοινό παράγοντα το z² και δεξιά το -3.
Φέρε τα όλα στο ένα μέλος και κάνε παραγοντοποίηση.
Ρίζες: z=±3i, z=2i.

Have fun και καλή επιτυχία.

Ευχαριστώ πολύ!!!
Άν και πρέπει να έκανες ένα λαθάκι στις ρίζες.
Δεν θα έπρεπε να είναι
${z}^{2}+3=0\Rightarrow {z}^{2}=-3\Rightarrow z=\pm i\sqrt{3}$

Ρε Δία,όχι και μάκμπουκ...
Εντάξει,ιεροσυλία

JKaradakov · 04-02-13

Αρχική Δημοσίευση από φρι:
Αχα . Μπορεί τελικά να αποδείξεις ότι ξ1=ξ2 αλλά δε σε νοιαζει

Το χρειαζόμουν σε μία άσκηση οπότε γι'αυτό με ένοιαζε.

Αρχική Δημοσίευση από Civilara:
Δεν είναι απαραίτητο να είναι ίσα αλλά ούτε και αποκλείεται. Για παράδειγμα η συνάρτηση f(x)=ημx+συνx, x ανήκει R. Η f είναι 2 φορές παραγωγίσιμη στο R με παρσγώγους:

f΄(x)=συνx-ημx
f΄΄(x)=-ημx-συνx=-f(x)

Λύνουμε τις εξισώσεις f(x)=0, f΄(x)=0, f΄΄(x)=0. (Οι εξισώσεις f(x)=0 και f΄΄(x)=0 είναι ισοδύναμες αφού f΄΄(x)=-f(x))

f΄΄(x)=0 <=> f(x)=0 <=> ημx+συνx=0 <=> ημx=-συνx <=> εφx=-1 <=> εφx=εφ(-π/4) <=> x=κπ-(π/4) όπου κ ανήκει Ζ
f΄(x)=0 <=> συνx-ημx=0 <=> ημx=συνx <=> εφx=1 <=> εφx=εφ(π/4) <=> x=λπ+(π/4) όπου λ ανήκει Ζ

Για να έχουν κοινές ρίζες οι εξισώσεις f΄(x)=0 και f΄΄(x)=0 πρέπει να υπάρχουν ακέραιοι κ,λ τέτοιοι ώστε:
κπ-(π/4)=λπ+(π/4) <=> κπ=λπ+(π/2) <=> κ=λ+(1/2) που είναι άτοπο αφού για κάθε λ ανήκει Ζ ο [λ+(1/2)] δεν είναι ακέραιος.

Για κ ανήκει Ζ έχουμε:
ημ(κπ+φ)=ημ(κπ)συνφ+συν(κπ)ημφ=0*συνφ+((-1)^|κ|)ημφ=[(-1)^|κ|]ημφ
συν(κπ+φ)=συν(κπ)συνφ-ημ(κπ)ημφ=((-1)^|κ|)συνφ-0*ημφ=[(-1)^|κ|]συνφ

Άρα
ημ(κπ-(π/4))=[(-1)^|κ|]ημ(-π/4)=-(SQRT(2)/2)*[(-1)^|κ|]
συν(κπ-(π/4))=[(-1)^|κ|]συν(-π/4)=(SQRT(2)/2)*[(-1)^|κ|]

ημ(κπ+(π/4))=[(-1)^|κ|]ημ(π/4)=(SQRT(2)/2)*[(-1)^|κ|]
συν(κπ+(π/4))=[(-1)^|κ|]συν(π/4)=(SQRT(2)/2)*[(-1)^|κ|]

f΄(κπ-(π/4))=(SQRT(2)/2)*[(-1)^|κ|]+(SQRT(2)/2)*[(-1)^|κ|]=SQRT(2)*[(-1)^|κ|] διάφορο 0
f΄΄(κπ-(π/4))=(SQRT(2)/2)*[(-1)^|κ|]-(SQRT(2)/2)*[(-1)^|κ|]=0

f΄(κπ+(π/4))=(SQRT(2)/2)*[(-1)^|κ|]-(SQRT(2)/2)*[(-1)^|κ|]=0
f΄΄(κπ+(π/4))=-(SQRT(2)/2)*[(-1)^|κ|]-(SQRT(2)/2)*[(-1)^|κ|]=-SQRT(2)*[(-1)^|κ|] διάφορο 0

Οι συναρτήσεις f, f΄ και f΄΄ είναι περιοδικές με περίοδο Τ=2π. Αυτό σημαίνει ότι για κάθε κ ανήκει Ζ* και για κάθε x ανήκει R ισχύουν:

f(x+2κπ)=f(x)
f΄(x+2κπ)=f΄(x)
f΄΄(x+2κπ)=f΄΄(x)

Η f είναι συνεχής στο διάστημα [x0+2κπ, x0+2(κ+1)π], παραγωγίσιμη στο (x0+2κπ, x0+2(κ+1)π) και ισχύει f(x0+2(κ+1)π)=f(x0+2κπ)=f(x0) για κάθε κ ανήκει Z και όπου x0 ανήκει R. Επομένως σύμφωνα με το θεώρημα Rolle υπάρχει τουλάχιστον ένα ξ1 στο διάστημα (x0+2κπ, x0+2(κ+1)π) τέτοιο ώστε f΄(ξ1)=0.

Η f΄ είναι συνεχής στο διάστημα [x0+2κπ, x0+2(κ+1)π], παραγωγίσιμη στο (x0+2κπ, x0+2(κ+1)π) και ισχύει f΄(x0+2(κ+1)π)=f΄(x0+2κπ)=f΄(x0) για κάθε κ ανήκει Z και όπου x0 ανήκει R. Επομένως σύμφωνα με το θεώρημα Rolle υπάρχει τουλάχιστον ένα ξ2 στο διάστημα (x0+2κπ, x0+2(κ+1)π) τέτοιο ώστε f΄΄(ξ2)=0.

Όμως επειδή οι εξισώσεις f΄(x)=0 και f΄΄(x)=0 δεν έχουν καμία κοινή ρίζα τότε ισχύει ξ1 διάφορο ξ2.

Ευχαρίστώ!

Αν και δεν χρειάζονταν τόσο αναλυτική λύση.

aris-bas · 5 Φεβρουαρίου 2013

1) δινεται η συναρτηση f με f(χ) ={ α(e^x), x<0
{ (χ^3)+β(χ^2)+γχ+β+γ, χ>=0
να υπολογισετε τα α,β,γ ε R ωστε να εφαρμοζεται το θεωρημα rolle για την f στο[-1,1] και να βρειτε ξ ε(-1,1) ωστε f'(ξ)=0

2)δινεται συναρτηση f:[α,β]->R παραγωγισιμη στο [α,β] οπου αβ διαφορο του μηδενος
εστω συναρτηση g με g(x)=f(x)[(x^2)-(α+β)x] ,η οποια ικανοποιει τις προυποθεσεις του θεωρηματος rolle στο [α,β]Να αποδειξετε οτι υπαρχει θ ε (α,β) τετοιο ωστε f'(θ)=0

3)εστω f συναρτηση ορισμενη και συνεχης στο [α,β],παραγωγισιμη στο (α,β) ωστε f(α)=f(β)=0
να αποδειξετε οτι για καθε $\gamma \quad \notin [\alpha ,\beta ]$ υπαρχει ξ ε (α,β) ωστε (ξ-γ)f'(ξ)=3f(ξ)

4)δινεται συναρτηση g δυο φορες παραγωγισιμη στο R ωστε να ισχυει 2g(x)+4xg'(x)+(x^2)g''(x) διαφορο του μηδενος για καθε χ ε R και g(0) διαφορο του μηδενος.Να αποδειξετε οτι η εξισωση g(x)=0 εχει το πολυ μια λυση στο R*.

μπορει να βοηθησει κανεις στις παραπανω????

ευχαριστω εκ των προτερων

υ.γ στην 1η ασκηση η συναρτηση ειναι δικλαδη

Civilara · 5 Φεβρουαρίου 2013

Αρχική Δημοσίευση από aris-bas:
4)δινεται συναρτηση g δυο φορες παραγωγισιμη στο R ωστε να ισχυει 2g(x)+4xg'(x)+(x^2)g''(x) διαφορο του μηδενος για καθε χ ε R και g(0) διαφορο του μηδενος.Να αποδειξετε οτι η εξισωση g(x)=0 εχει το πολυ μια λυση στο R*.

Θεωρούμε την συνάρτηση f με τύπο f(x)=(x^2)g(x) και πεδίο ορισμού το Α=R.

Επειδή η g είναι 2 φορές παραγωγίσιμη στο R τότε και η f είναι 2 φορές παραγωγίσιμη στο R με παραγώγους:
f΄(x)=2xg(x)+(x^2)g΄(x)=x[2g(x)+xg΄(x)], x ανήκει R
f΄΄(x)=2g(x)+4xg΄(x)+(x^2)g΄΄(x), x ανήκει R

Έχουμε
f(0)=(0^2)*g(0)=0
f΄(0)=0*[2g(0)+0*g΄(0)]=0
f΄΄(0)=2g(0)+4*0*g΄(0)+(0^2)*g΄΄(0)=2g(0) διάφορο 0 εφόσον g(0) διάφορο 0

Η f είναι 2 φορές παραγωγίσιμη στο R οπότε η f και η f΄ είναι συνεχείς στο R

Για κάθε x<0, η f΄ είναι συνεχής στο [x,0] και παραγωγίσιμη στο (x,0). Επομένως σύμφωνα με το θεώρημα μέσης τιμής υπάρχει τουλάχιστον ένα ξ1 ανήκει (x,0) τέτοιο ώστε:
f΄΄(ξ1)=[f΄(0)-f΄(x)]/(0-x)=f΄(x)/x=2g(x)+xg΄(x)

Για κάθε x>0, η f΄ είναι συνεχής στο [0,x] και παραγωγίσιμη στο (0,x). Επομένως σύμφωνα με το θεώρημα μέσης τιμής υπάρχει τουλάχιστον ένα ξ2 ανήκει (0,x) τέτοιο ώστε:
f΄΄(ξ2)=[f΄(x)-f΄(0)]/(x-0)=f΄(x)/x=2g(x)+xg΄(x)

Άρα για κάθε x ανήκει R* υπάρχει τουλάχιστον ένα ξ διάφορο x και διάφορο 0 τέτοιο ώστε f΄΄(ξ)=2g(x)+xg(x)
Επίσης επειδή f΄΄(0)=2g(0), η παραπάνω σχέση ικανοποιείται για ξ=x=0.

Επομένως για κάθε x ανήκει R υπάρχει τουλάχιστον ένα ξ ανήκει R τέτοιο ώστε f΄΄(ξ)=2g(x)+xg(x)

f΄΄(ξ) διάφορο 0 => 2g(x)+xg(x) διάφορο 0 για κάθε x ανήκει R
(Για x=0 προκύπτει g(0) διάφορο 0 που δίνεται. Επομένως δεν είναι απαραίτητο να δίνεται στην εκφώνηση ότι g(0) διάφορο 0 αφού προκύπτει)

Επειδή f΄(x)=x[2g(x)+xg΄(x)] τότε ισχύει f΄(x) διάφορο 0 για κάθε x ανήκει R*.

Για κάθε x<0, η f είναι συνεχής στο [x,0] και παραγωγίσιμη στο (x,0). Επομένως σύμφωνα με το θεώρημα μέσης τιμής υπάρχει τουλάχιστον ένα ξ3 ανήκει (x,0) τέτοιο ώστε:
f΄(ξ3)=[f(0)-f(x)]/(0-x)=f(x)/x=xg(x)

Για κάθε x>0, η f είναι συνεχής στο [0,x] και παραγωγίσιμη στο (0,x). Επομένως σύμφωνα με το θεώρημα μέσης τιμής υπάρχει τουλάχιστον ένα ξ4 ανήκει (0,x) τέτοιο ώστε:
f΄(ξ4)=[f(x)-f(0)]/(x-0)=f(x)/x=xg(x)

Άρα για κάθε x ανήκει R* υπάρχει τουλάχιστον ένα ξ΄ διάφορο x και διάφορο 0 τέτοιο ώστε f΄(ξ΄)=xg(x).

Έχουμε
f΄(ξ΄) διάφορο 0 => xg(x) διάφορο 0 => g(x) διάφορο 0 για κάθε x ανήκει R*

Επειδή g(x) διάφορο 0 για κάθε x ανήκει R* και g(0) διάφορο 0 τότε g(x) διάφορο 0 για κάθε x ανήκει R.

Επομένως η εξίσωση g(x)=0 δεν έχει καμία πραγματική λύση.

Civilara · 05-02-13

Αρχική Δημοσίευση από aris-bas:
3)εστω f συναρτηση ορισμενη και συνεχης στο [α,β],παραγωγισιμη στο (α,β) ωστε f(α)=f(β)=0
να αποδειξετε οτι για καθε $\gamma \quad \notin [\alpha ,\beta ]$ υπαρχει ξ ε (α,β) ωστε (ξ-γ)f'(ξ)=3f(ξ)

Θεωρούμε τη συνάρτηση g με τύπο g(x)=f(x)/[(x-γ)^3] όπου x ανήκει [α,β] και γ δεν ανήκει [α,β].
Επειδή η f είναι συνεχής στο [α,β] τότε και η g είναι συνεχής στο [α,β].

Έχουμε g(α)=f(α)/[(α-γ)^3]=0 και g(β)=f(β)/[(β-γ)^3]=0. Επομένως g(α)=g(β)=0.

Επειδή η f είναι παραγωγίσιμη στο (α,β) τότε και η g είναι παραγωγίσιμη στο (α,β) με πρώτη παράγωγο:

g΄(x)=[f΄(x)(x-γ)-3f(x)]/[(x-γ)^4], x ανήκει (α,β)

Η g είναι συνεχής στο [α,β], παραγωγίσιμη στο (α,β) και ισχύει g(α)=g(β). Επομένως σύμφωνα με το θεώρημα Rolle υπάρχει τουλάχιστον ένα ξ ανήκει (α,β) τέτοιο ώστε g΄(ξ)=0. Έχουμε:

g΄(ξ)=0 <=> [f΄(ξ)(ξ-γ)-3f(ξ)]/[(ξ-γ)^4]=0 <=> f΄(ξ)(ξ-γ)-3f(ξ)=0 <=> f΄(ξ)(ξ-γ)=3f(ξ)

greekgohan · 05-02-13

Αρχική Δημοσίευση από aris-bas:
2)δινεται συναρτηση f:[α,β]->R παραγωγισιμη στο [α,β] οπου αβ διαφορο του μηδενος
εστω συναρτηση g με g(x)=f(x)[(x^2)-(α+β)x] ,η οποια ικανοποιει τις προυποθεσεις του θεωρηματος rolle στο [α,β]Να αποδειξετε οτι υπαρχει θ ε (α,β) τετοιο ωστε f'(θ)=0

Eφοσον η g ικανοποιει τις προυποθεσεις του rolle στο [α,β],αρα g(α)=g(β) κατι που οδηγει σε f(α)=f(β).
Δηλαδη παρατηρουμε οτι και η f ικανοποιει τις προυποθεσεις του rolle,συνεπως υπαρχει θ στο(α,β) ωστε f'(θ)=0.

rebel · 5 Φεβρουαρίου 2013

Αρχική Δημοσίευση από aris-bas:
4)δινεται συναρτηση g δυο φορες παραγωγισιμη στο R ωστε να ισχυει 2g(x)+4xg'(x)+(x^2)g''(x) διαφορο του μηδενος για καθε χ ε R και g(0) διαφορο του μηδενος.Να αποδειξετε οτι η εξισωση g(x)=0 εχει το πολυ μια λυση στο R*.

Θεωρώ την συνάρτηση $h(x)=x^2g(x)$ . Ας υποθέσουμε ότι η g έχει δύο ρίζες $\rho_1 , \rho_2$ διαφορετικές από το μηδέν (αφού $g(0) \neq 0$ ) και ότι χωρίς βλάβη είναι $0<\rho_1< \rho_2$ (οι περιπτώσεις $\rho_1< 0 < \rho_2 , \rho_1< \rho_2<0$ αντιμετωπίζονται με τον ίδιο ακριβώς τρόπο)
Είναι τότε $h(0)=h(\rho_1)=h(\rho_2)=0$ . Από Rolle υπάρχουν $x_1 \in (0, \rho_1) ,\,\,x _2 \in (\rho_1, \rho_2)$ με $h'(x_1)=h'(x_2)=0$ . Και πάλι από Rolle υπάρχει $\xi \in (x_1, x_2)$ με $h''(\xi)=0$ . Άτοπο λόγω της υπόθεσης. Άρα η g έχει το πολύ μία ρίζα στο $\mathbb{R}^*$

t00nS · 06-02-13

1) Εστω ολοκλήρωμα απο 0 εώς χ^2 f(t-π/3)dt +συνχ^2>=1 να υπολογιστεί το f(-π/3)
2)να υπολογιστεί το ολοκλήρωμα απο 0 εώς π/2 (συν^3*χ-2συνχ)*ημχdx

Civilara · 6 Φεβρουαρίου 2013

Αρχική Δημοσίευση από aris-bas:
1) δινεται η συναρτηση f με f(χ) ={ α(e^x), x<0
{ (χ^3)+β(χ^2)+γχ+β+γ, χ>=0
να υπολογισετε τα α,β,γ ε R ωστε να εφαρμοζεται το θεωρημα rolle για την f στο[-1,1] και να βρειτε ξ ε(-1,1) ωστε f'(ξ)=0

Θεωρούμε την συνάρτηση g(x)=α(e^x), x ανήκει R. Η g είναι συνεχής και παραγωγίσιμη στο R με πρώτη παράγωγο:
g΄(x)=α(e^x), x ανήκει R

Έχουμε g(0)=g΄(0)=α. Επειδή η g είναι συνεχής και παραγωγίσιμη στο 0 έχουμε:

lim(x->0)g(x)=g(0)=α <=> lim(x->0-)g(x)=lim(x->0+)g(x)=α
lim(x->0)[(g(x)-g(0))/(x-0)]=g΄(0)=α <=> lim(x->0-)[(g(x)-g(0))/(x-0)]=lim(x->0+)[(g(x)-g(0))/(x-0)]=α

Θεωρούμε την συνάρτηση h(x)=(x^3)+β(x^2)+γx+β+γ, x ανήκει R. Η h είναι συνεχής και παραγωγίσιμη στο R με πρώτη παράγωγο:
h΄(x)=3(x^2)+2βx+γ, x ανήκει R

Έχουμε h(0)=β+γ και h΄(0)=γ. Επειδή η h είναι συνεχής και παραγωγίσιμη στο 0 έχουμε:

lim(x->0)h(x)=h(0)=β+γ <=> lim(x->0)h(x)=lim(x->0+)h(x)=β+γ
lim(x->0)[(h(x)-h(0))/(x-0)]=h΄(0)=γ <=> lim(x->0-)[(h(x)-h(0))/(x-0)]=lim(x->0+)[(h(x)-h(0))/(x-0)]=γ

Για την συνάρτηση f γνωρίζουμε ότι:
f(x)=g(x) για x<0
f(x)=h(x) για x>=0

Επειδή για κάθε x ανήκει (-οο,0) ισχύει f(x)=g(x) τότε η f είναι συνεχής και παραγωγίσιμη στο (-οο,0) με πρώτη παράγωγο f΄(x)=g΄(x) για κάθε x ανήκει (-οο,0). Επειδή για κάθε x ανήκει (0,+οο) ισχύει f(x)=h(x) τότε η f είναι συνεχής και παραγωγίσιμη στο (0,+oo) με πρώτη παράγωγο f΄(x)=h΄(x) για κάθε x ανήκει (0,=oo).

Για να εφαρμόζεται για την f το θεώρημα του Rolle στο διάστημα [-1,1] πρέπει η f να είναι συνεχής στο [-1,1], παραγωγίσιμη στο (-1,1) και να ισχύει f(-1)=f(1). Για να είναι η f συνεχής στο [-1,1] και παραγωγίσιμη στο (-1,1) πρέπει η f να είναι παραγωγίσιμη στο x0=0 (οπότε θα είναι και συνεχής στο x0=0) καθώς είναι συνεχής και παραγωγίσιμη στο R*.

Για να είναι η f συνεχής στο x0=0 πρέπει να υπάρχει το lim(x->0)f(x) και να ισούται με f(0).

Έχουμε:
lim(x->0-)f(x)=lim(x->0-)g(x)=g(0)=α
lim(x->0+)f(x)=lim(x->0+)h(x)=β+γ

Για να υπάρχει το lim(x->0)f(x) πρέπει να ισχύει lim(x->0-)f(x)=lim(x->0+)f(x). Έχουμε
lim(x->0-)f(x)=lim(x->0+)f(x) <=> α=β+γ

Επομένως έχουμε:
g(x)=(β+γ)(e^x)
h(x)=(x^3)+β(x^2)+γx+β+γ

Άρα έχουμε lim(x->0)f(x)=(β+γ) και f(0)=β+γ. Άρα lim(x->0)f(x)=f(0) που σημαίνει ότι η f είναι συνεχής στο x0=0 για α=β+γ

Στη συνέχεια θα ελεγχθεί η παραγωγισιμότητα της f στο x0=0. Έχουμε:

lim(x->0-)[(f(x)-f(0))/(x-0)]=lim(x->0-)[(g(x)-g(0))/(x-0)]=α=β+γ
lim(x->0+)[(f(x)-f(0))/(x-0)]=lim(x->0+)[(h(x)-h(0))/(x-0)]=γ

Για να είναι η f παραγωγίσιμη στο x0=0 πρέπει ισχύει:
lim(x->0-)[(f(x)-f(0))/(x-0)]=lim(x->0+)[(f(x)-f(0))/(x-0)] <=> β+γ=γ <=> β=0

Επομένως έχουμε:
g(x)=γ(e^x)
h(x)=(x^3)+γx+γ

Επομένως για β=0 προκύπτει:

lim(x->0-)[(f(x)-f(0))/(x-0)]=lim(x->0+)[(f(x)-f(0))/(x-0)]=γ <=> lim(x->0)[(f(x)-f(0))/(x-0)]=γ
Άρα η f είναι παραγωγίσιμη στο x0=0 με παράγωγο f΄(0)=γ

Έχουμε:
f(-1)=g(-1)=γ(e^(-1))=γ/e
f(1)=h(1)=(1^3)+γ*1+γ=1+2γ

Επειδή f(-1)=f(1) έχουμε:
γ/e=1+2γ <=> γ=e+2eγ <=> (2e-1)γ=-e <=> γ=-e/(2e-1)
Άρα α=β+γ => α=0+γ=γ => α=γ=-e/(2e-1)

Τελικά έχουμε:
β=0
α=γ=-e/(2e-1)

Συνεπώς
g(x)=-(e^(x+1))/(2e-1)
h(x)=(x^3)-[e/(2e-1)]x-[e/(2e-1)]

Για x<0 είναι f΄(x)=g΄(x)=-(e^(x+1))/(2e-1)<0 για κάθε x ανήκει (-οο,0)
Για x=0 είναι f΄(0)=γ=-e/(2e-1)<0
Για x>0 είναι f΄(x)=h΄(x)=3(x^2)-[e/(2e-1)]=3{x+SQRT[e/(3(2e-1))]}{x-SQRT[e/(3(2e-1))]}

Επειδή ισχύει 0<SQRT[e/(3(2e-1))]<1 (απλή η απόδειξη) τότε έχουμε -1<-ξ<0<ξ<1 όπου

ξ=SQRT[e/(3(2e-1))]

και ισχύει f΄(-ξ)=f΄(ξ)=0

Civilara · 6 Φεβρουαρίου 2013

Αρχική Δημοσίευση από t00nS:
1) Εστω ολοκλήρωμα απο 0 εώς χ^2 f(t-π/3)dt +συνχ^2>=1 να υπολογιστεί το f(-π/3)

Δεν είναι σαφής η εκφώνηση όπως την έχεις γράψει και δεν δίνεται το πεδίο ορισμού της f. Γι αυτό θεωρώ ότι η f είναι συνεχής στο [-π/3,+οο) και ότι για κάθε x ανήκει [-π/3,+οο) ισχύει:

$\sigma \upsilon \nu \left({x}^{2} \right)+\int_{0}^{{x}^{2}}f\left(t-\frac{\pi }{3} \right)dt\geq 1$

Θεωρούμε την συνάρτηση F με τύπο
$F(x)=\int_{0}^{x}f(u)du$

Επειδή η f είναι συνεχής στο [-π/3,+οο) τότε η F είναι παραγωγίσιμη στο [-π/3,+οο) με πρώτη παράγωγο F΄(x)=f(x) για κάθε x ανήκει [-π/3,+οο).

Θεωρούμε την αλλαγή μεταβλητής u=t-(π/3) <=> t=u+(π/3) => dt=du
u2=(x^2)-(π/3)
u1=-(π/3)

Η αρχική ανισότητα γράφεται ισοδύναμα

$\sigma \upsilon \nu \left({x}^{2} \right)+\int_{-\frac{\pi }{3}}^{{x}^{2}-\frac{\pi }{3}}F'(u)du\geq 1\Leftrightarrow \sigma \upsilon \nu \left({x}^{2} \right)+F\left({x}^{2}-\frac{\pi }{3} \right)-F\left(-\frac{\pi }{3} \right)\geq 1$

Θεωρούμε y=(x^2)-(π/3)>=-(π/3) για κάθε x ανήκει R, οπότε η ανισότητα γράφεται ισοδύναμα
$\sigma \upsilon \nu \left(y+\frac{\pi }{3} \right)+F\left(y \right)-F\left(-\frac{\pi }{3} \right)\geq 1$
όπου y ανήκει [-π/3,+οο)

Άρα ισχύει
$\sigma \upsilon \nu \left(x+\frac{\pi }{3} \right)+F\left(x \right)-F\left(-\frac{\pi }{3} \right)\geq 1$
για κάθε x ανήκει [-π/3,+οο)

Θεωρούμε την συνάρτηση g με τύπο:
$g(x)=\sigma \upsilon \nu \left(x+\frac{\pi }{3} \right)+F\left(x \right)-F\left(-\frac{\pi }{3} \right)$

Επειδή η F είναι παραγωγίσιμη στο [-π/3,+οο) τότε η g είναι παραγωγίσιμη στο [-π/3,+οο) με πρώτη παράγωγο:
$g(x)=-\eta \mu \left(x+\frac{\pi }{3} \right)+F'(x)=-\eta \mu \left(x+\frac{\pi }{3} \right)+f(x)$

Έχουμε g(-π/3)=1 και g΄(-π/3)=F'(-π/3)=f(-π/3) και για κάθε x>=-(π/3) ισχύει g(x)>=1 => g(x)>=g(-π/3)

Η g είναι ορισμένη στο [-π/3,+οο), παραγωγίσιμη στο x0=-π/3 και ισχύει g(x)>=g(-π/3) για κάθε x>=-π/3 που σημαίνει ότι η g παρουσιάζει ολικό ελάχιστο στο x0=-π/3. Επομένως σύμφωνα με το θεώρημα Fermat ισχύει g΄(-π/3)>=0 => f(-π/3)>=0

Σημείωση: Δεν μπορούμε να βγάλουμε το συμπέρασμα f(-π/3)=0 καθώς το x0=-π/3 είναι άκρο διαστήματος για το οποίο ισχύει η ανισότητα g(x)>=g(-π/3). Αν υπήρχε α<-π/3 έτσι ώστε g(x)>=g(-π/3) για κάθε x>=α τότε θα μπορούσαμε να βγάλουμε το συμπέρασμα f΄(-π/3)=0 .

lowbaper92 · 06-02-13

Αρχική Δημοσίευση από t00nS:
2)να υπολογιστεί το ολοκλήρωμα απο 0 εώς π/2 (συν^3*χ-2συνχ)*ημχdx

$\int \left({\sigma \upsilon \nu }^{3}x \cdot \eta \mu x\right)dx-\int\left( 2\cdot\eta \mu x\cdot \sigma \upsilon \nu x \right)dx=-\frac{{\sigma \upsilon \nu }^{4}x}{4}+{\sigma \upsilon \nu }^{2}x+c$

Αν δεν το προσέξεις αυτό κατευθείαν, θέσε u=συνx

t00nS · 06-02-13

Αρχική Δημοσίευση από Civilara:
Δεν είναι σαφής η εκφώνηση όπως την έχεις γράψει και δεν δίνεται το πεδίο ορισμού της f. Γι αυτό θεωρώ ότι η f είναι συνεχής στο [-π/3,+οο) και ότι για κάθε x ανήκει [-π/3,+οο) ισχύει:

$\sigma \upsilon \nu \left({x}^{2} \right)+\int_{0}^{{x}^{2}}f\left(t-\frac{\pi }{3} \right)dt\geq 1$

Θεωρούμε την συνάρτηση F με τύπο
$F(x)=\int_{0}^{x}f(u)du$

Επειδή η f είναι συνεχής στο [-π/3,+οο) τότε η F είναι παραγωγίσιμη στο [-π/3,+οο) με πρώτη παράγωγο F΄(x)=f(x) για κάθε x ανήκει [-π/3,+οο).

Θεωρούμε την αλλαγή μεταβλητής u=t-(π/3) <=> t=u+(π/3) => dt=du
u2=(x^2)-(π/3)
u1=-(π/3)

Η αρχική ανισότητα γράφεται ισοδύναμα

$g\sigma \upsilon \nu \left({x}^{2} \right)+\int_{-\frac{\pi }{3}}^{{x}^{2}-\frac{\pi }{3}}F΄(u)du\geq 1\Leftrightarrow \sigma \upsilon \nu \left({x}^{2} \right)+F\left({x}^{2}-\frac{\pi }{3} \right)-F\left(-\frac{\pi }{3} \right)\geq 1$

Θεωρούμε y=(x^2)-(π/3)>=-(π/3) για κάθε x ανήκει R, οπότε η ανισότητα γράφεται ισοδύναμα
$\sigma \upsilon \nu \left(y+\frac{\pi }{3} \right)+F\left(y \right)-F\left(-\frac{\pi }{3} \right)\geq 1$
όπου y ανήκει [-π/3,+οο)

Άρα ισχύει
$\sigma \upsilon \nu \left(x+\frac{\pi }{3} \right)+F\left(x \right)-F\left(-\frac{\pi }{3} \right)\geq 1$
για κάθε x ανήκει [-π/3,+οο)

Θεωρούμε την συνάρτηση g με τύπο:
$g(x)=\sigma \upsilon \nu \left(x+\frac{\pi }{3} \right)+F\left(x \right)-F\left(-\frac{\pi }{3} \right)$

Επειδή η F είναι παραγωγίσιμη στο [-π/3,+οο) τότε η g είναι παραγωγίσιμη στο [-π/3,+οο) με πρώτη παράγωγο:
$g(x)=-\eta \mu \left(x+\frac{\pi }{3} \right)+F'(x)=-\eta \mu \left(x+\frac{\pi }{3} \right)+f(x)$

Έχουμε g(-π/3)=1 και g΄(-π/3)=F'(-π/3)=f(-π/3) και για κάθε x>=-(π/3) ισχύει g(x)>=1 => g(x)>=g(-π/3)

Η g είναι ορισμένη στο [-π/3,+οο), παραγωγίσιμη στο x0=-π/3 και ισχύει g(x)>=g(-π/3) για κάθε x>=-π/3 που σημαίνει ότι η g παρουσιάζει ολικό ελάχιστο στο x0=-π/3. Επομένως σύμφωνα με το θεώρημα Fermat ισχύει g΄(-π/3)>=0 => f(-π/3)>=0

Σημείωση: Δεν μπορούμε να βγάλουμε το συμπέρασμα f(-π/3)=0 καθώς το x0=-π/3 είναι άκρο διαστήματος για το οποίο ισχύει η ανισότητα g(x)>=g(-π/3). Αν υπήρχε α<-π/3 έτσι ώστε g(x)>=g(-π/3) για κάθε x>=α τότε θα μπορούσαμε να βγάλουμε το συμπέρασμα f΄(-π/3)=0 .

θα μπορούσα ακόμα να θέσω αυτό το ολοκλήρωμα έστω f(x) όπου f(χ) παραγωγίσιμη ως πράξη παραγωγισίμων και μετά να δω αμα ενφανίζει τοπικό ελάχιστο ή τοπικό μέγιστο και υστερα Θ.fermat?

Civilara · 06-02-13

Αρχική Δημοσίευση από t00nS:
θα μπορούσα ακόμα να θέσω αυτό το ολοκλήρωμα έστω f(x) όπου f(χ) παραγωγίσιμη ως πράξη παραγωγισίμων και μετά να δω αμα ενφανίζει τοπικό ελάχιστο ή τοπικό μέγιστο και υστερα Θ.fermat?

Ως F(x) ή g(x) γιατί f(x) είναι μέσα στο ολοκλήρωμα. Ναι θα μπορούσες. Κάντο για εξάσκηση.

Mercury · 07-02-13

Απορία:
$f(z)=\frac{3+4i}{6}z+\frac{5}{6}\bar{z}$
Να δείξετε ότι $f(f(z))=f(z)$
Μπορεί κάποιος να μου πει πως θα γραφεί το $f(f(z))$ ,γιατί κόλλησα λιγάκι...

antwwwnis · 07-02-13

Όπου z θα βαλεις το f(z).

Βοήθεια/Aπορίες στα Μαθηματικά Προσανατολισμού

Διάσημο μέλος

Περιβόητο μέλος

Επιφανές μέλος

Διάσημο μέλος

Επιφανές μέλος

Επιφανές μέλος

Τιμώμενο Μέλος

Νεοφερμένος

Περιβόητο μέλος

Περιβόητο μέλος

Εκκολαπτόμενο μέλος

Πολύ δραστήριο μέλος

Εκκολαπτόμενο μέλος

Περιβόητο μέλος

Περιβόητο μέλος

Πολύ δραστήριο μέλος

Εκκολαπτόμενο μέλος

Περιβόητο μέλος

Επιφανές μέλος

Διάσημο μέλος