Βοήθεια/Aπορίες στα Μαθηματικά Προσανατολισμού

IasonasM · 03-01-13

Λέει πως ισχύει η
"(για κάθε x e A, [f(x)]^2=[g(x)]^2) <=> (για κάθε x e A, f(x)=g(x))" (στην συγκεκριμένη , g(x)=x )
Όμως αυτό δεν ισχύει αφού το (για κάθε x e A, [f(x)]^2=x^2) ισχύει και για μία συνάρτηση διάφορη της f(x)=x. Πχ μία με διακλάδωση
f(x) = { x για x>3 , -x για x<=3 }
Οι δύο ισοδυναμίες δεν είναι ισοδύναμες, έχουν αλλού είναι το "ή". (Τουλάχιστον έτσι είχα δει από ένα .pdf από το mathematica για ποσοδείκτες κλπ )

sokratis lyras · 03-01-13

Αρχική Δημοσίευση από IasonasM:
σίγουρα;
η ισοδυναμία "(για κάθε x e A, [f(x)]^2=[g(x)]^2 ) <=> (για κάθε x e A, f(x)=g(x) ) ή (για κάθε x e A, f(x)=-g(x) ) "
δεν είναι λάθος;
(η σωστή δεν είναι "(για κάθε x e A, [f(x)]^2=[g(x)]^2 ) <=> (για κάθε x e A, f(x)=g(x) ή f(x)=-g(x) ) " ; )

Όχι,καμία από τις 2 δεν είναι σωστές.Αν f,g συνεχείς και $f^2(x)=g^2(x)$ για κάθε x στο Α τότε ισχύει $f(x)=g(x)$ για κάποια $x\in A$ και $f(x)=-g(x)$ για τα υπόλοιπα(εκτός αν υπάρχουν επιπλέον συνθήκες στην άσκηση και η μια περίπτωση απορρίπτεται).

IasonasM · 03-01-13

Αρχική Δημοσίευση από sokratis lyras:
Όχι,καμία από τις 2 δεν είναι σωστές.Αν f,g συνεχείς και $f^2(x)=g^2(x)$ για κάθε x στο Α τότε ισχύει $f(x)=g(x)$ για κάποια $x\in A$ και $f(x)=-g(x)$ για τα υπόλοιπα(εκτός αν υπάρχουν επιπλέον συνθήκες στην άσκηση και η μια περίπτωση απορρίπτεται).

το bold δεν είναι ίδιο με το "(για κάθε x e A, f(x)=g(x) ή f(x)=-g(x) )" ;

sokratis lyras · 03-01-13

Αρχική Δημοσίευση από IasonasM:
σίγουρα;
η ισοδυναμία "(για κάθε x e A, [f(x)]^2=[g(x)]^2 ) <=> (για κάθε x e A, f(x)=g(x) ) ή (για κάθε x e A, f(x)=-g(x) ) "
δεν είναι λάθος;
(η σωστή δεν είναι "(για κάθε x e A, [f(x)]^2=[g(x)]^2 ) <=> (για κάθε x e A, f(x)=g(x) ή f(x)=-g(x) ) " ; )

Αρχική Δημοσίευση από IasonasM:
το bold δεν είναι ίδιο με το "(για κάθε x e A, f(x)=g(x) ή f(x)=-g(x) )" ;

Εγώ κατάλαβα ότι ή για όλα τα x θα ισχύει το ένα ή για όλα τα x θα ισχύει το άλλο.Ίσως το παρεξήγησα.Πάντως για κάθε ενδεχόμενο θα συνιστούσα να το αναφέρετε όπως το bold παραπάνω που είναι ξεκάθαρο.

ξαροπ · 03-01-13

^ Κι εγώ το παραπάνω κατάλαβα έτσι όπως ήταν αρχικά γραμμένο.

vivianouz · 03-01-13

καλησπερα!!!!Μηπως μπορει να βοηθησει κανεις στα παρακατω θεματακια...???
1)έστω η παραγωγίσιμη συνάρτηση στο [α,β] με $f'(x)\neq 0$ για κάθε $x\in [\alpha ,\beta ]$
να δείξετε ότι:
α) $f(\alpha )\neq f(\beta )$
β)υπάρχει $x_{0}\in (\alpha ,\beta )$ τέτοιο ώστε $7f(x_{0})=3f(\alpha )+4f(\beta )$
γ)υπαρχουν $x_{1}\in (\alpha ,x_{0})$ και $x_{2}\in (x_{0},\beta )$ τέτοια ώστε $f'(x_{1})\cdot f'(x_{2})>0$
δ)αν για την $f:R\rightarrow R$ ισχύει επιπλέον ότι $f'(x)<0$ για κάθε $x\in R$ ,να δείξετε ότι η εξίσωση $f(x)=x$ έχει τουλάχιστον μια λύση στο $R$

2)δίνονται οι μιγαδικοί αριθμοί $z=1+i\alpha ^{x},w=x+1+i$ και η συνάρτηση $f(x)=|z|^{2}x+|w-1|^{2}$ με $x\in R$ και $\alpha >0$ .Αν ισχύει $|z-\bar{w}|\leq |\bar{z}+w|$ , τότε:
α)να δείξετε ότι $\alpha =e$
β)να βρείτε τα $\lim x_{\rightarrow -\propto } , \lim x_{\rightarrow +\propto }$
γ)να δείξετε ότι η $Cf$ δεν έχει ασύμπτωτες
δ)να δείξετε ότι η εξίσωση $f(x)=0$ είναι αδύνατη στο $R$

3)δίνεται η συνάρτηση $f:R\rightarrow R$ η οποία είναι παραγωγίσιμη στο $R$ και για την οποία ισχύουν:
$\bullet f'(0)=1$
$\bullet f(x+y)=f(x)f(y)e^{2xy}$ για κάθε $x,y\in R$
να δείξετε ότι:
α) $f(0)=1$
β) $f'(x)=(2x+1)f(x),x\in R$
γ)η συνάρτηση $g(x)=\frac{f(x)}{e^{^{x^{2}+x}}}$ είναι σταθερή στο $R$
δ) $f(x)={e^{^{x^{2}+x}}},x\in R$
ε)η $Cf$ δεν έχει ασύμπτωτες
στ)η $Cf$ δεν έχει σημεία καμπής
ζ)η ευθεία $y=3x+5$ τέμνει τη $Cf$ σε μοναδικό σημείο με τετμημένη $x_{0}\in (1,2)$
η) $e^{x}\geq x+1,x\in R$ και $f(x)\geq x^{2}+x+1,x\in R$ .

Just a sweetie!! · 03-01-13

Σας ευχαριστω όλους πάρα πολύ :-) γενικά κατέληξα στο συμπέρασμα οτι αν γνωρίζουμε μια σχέση [f(x)]^ν=[g(x)]^ν, η οποία ισχύει για κάθε x του πεδίου ορισμού, αν ν περιττός μπορούμε να καταλήξουμε στο συμπέρασμα f(x)=g(x) για κάθε x του πεδίου ορισμού. Αντίθετα, αν ν αρτιος, δεν μπορούμε να καταλήξουμε σε συμπέρασμα σχετικά με τον τύπο της f πχ, αν αυτή είναι ζητούμενη κ η g γνωστή. Απλα γνωρίζουμε κάτι για κάποια x μόνο του πεδίου ορισμού της, για τον προσδιορισμό των οποίων, άρα κ της f απαιτούνται επιπλέον δεδομένα.

rebel · 4 Ιανουαρίου 2013

Αρχική Δημοσίευση από Just a sweetie!!:
για τον προσδιορισμό των οποίων, άρα κ της f απαιτούνται επιπλέον δεδομένα.

Αν δίνεται η συνέχεια της f ξέρεις ότι διατηρεί πρόσημο άρα f(x)=x για όλα τα χ ή f(x)=-x για όλα τα χ. Αν επιπλέον ξέρεις και μία τιμή της f, τότε από το πρόσημό της καταλαβαίνεις ποιος από τους δύο τύπους είναι ο σωστός για την f.

Υ.Γ.: Φυσικά η $f$ πρέπει να είναι ορισμένη σε διάστημα που δεν περιέχει το 0, αλλιώς δεν θα είναι μη μηδενική αφού f(0)=0.

rebel · 4 Ιανουαρίου 2013

Αρχική Δημοσίευση από vivianouz:
καλησπερα!!!!Μηπως μπορει να βοηθησει κανεις στα παρακατω θεματακια...???
1)έστω η παραγωγίσιμη συνάρτηση στο [α,β] με $f'(x)\neq 0$ για κάθε $x\in [\alpha ,\beta ]$
να δείξετε ότι:
α) $f(\alpha )\neq f(\beta )$
β)υπάρχει $x_{0}\in (\alpha ,\beta )$ τέτοιο ώστε $7f(x_{0})=3f(\alpha )+4f(\beta )$
γ)υπαρχουν $x_{1}\in (\alpha ,x_{0})$ και $x_{2}\in (x_{0},\beta )$ τέτοια ώστε $f'(x_{1})\cdot f'(x_{2})>0$
δ)αν για την $f:R\rightarrow R$ ισχύει επιπλέον ότι $f'(x)<0$ για κάθε $x\in R$ ,να δείξετε ότι η εξίσωση $f(x)=x$ έχει τουλάχιστον μια λύση στο $R$

α) Αν ήταν $f(a)=f(b)$ τότε από Rolle θα υπήρχε $\xi \in (a,b):f'(\xi)=0$ , άτοπο απ' την υπόθεση.
β) Χωρίς βλάβη της γενικότητας υποθέτουμε ότι $f(a)<f(b)$ ( εντελώς όμοια βγαίνει και για $f(a)>f(b)$ ). Εύκολα επαληθεύεται ότι
$f(a)<\frac{3f(a)+4f(b)}{7}<f(b)$
και αφού η f είναι συνεχής στο [a,b], από το θεώρημα ενδιαμέσων τιμών θα υπάρχει
$x_0 \in (a,b):f(x_0)=\frac{3f(a)+4f(b)}{7}$
γ) Προφανές από Θ.Μ.Τ. στα διαστήματα $[a,x_0],\,\,[x_0,b]$

δ) Αν $f(0)=0$ το ζητούμενο είναι προφανές.
Αν $f(0)>0$ τότε αφού η $f$ είναι γνησίως φθίνουσα είναι $f(f(0))<f(0)$ . Με Bolzano για την $g(x)=f(x)-x$ στο διάστημα $[0,f(0)]$ έπεται το ζητούμενο.
Αν $f(0)<0$ τότε αφού η $f$ είναι γνησίως φθίνουσα είναι $f(f(0))>f(0)$ . Με Bolzano για την $g(x)=f(x)-x$ στο διάστημα $[f(0),0]$ έπεται το ζητούμενο.

vivianouz · 5 Ιανουαρίου 2013

Αρχική Δημοσίευση από styt_geia:
α) Αν ήταν $f(a)=f(b)$ τότε από Rolle θα υπήρχε $\xi \in (a,b):f'(\xi)=0$ , άτοπο απ' την υπόθεση.
β) Χωρίς βλάβη της γενικότητας υποθέτουμε ότι $f(a)<f(b)$ ( εντελώς όμοια βγαίνει και για $f(a)>f(b)$ ). Εύκολα επαληθεύεται ότι
$f(a)<\frac{3f(a)+4f(b)}{7}<f(b)$
και αφού η f είναι συνεχής στο [a,b], από το θεώρημα ενδιαμέσων τιμών θα υπάρχει
$x_0 \in (a,b):f(x_0)=\frac{3f(a)+4f(b)}{7}$
γ) Προφανές από Θ.Μ.Τ. στα διαστήματα $[a,x_0],\,\,[x_0,b]$

δ) Αν $f(0)=0$ το ζητούμενο είναι προφανές.
Αν $f(0)>0$ τότε αφού η $f$ είναι γνησίως φθίνουσα είναι $f(f(0))<f(0)$ . Με Bolzano για την $g(x)=f(x)-x$ στο διάστημα $[0,f(0)]$ έπεται το ζητούμενο.
Αν $f(0)<0$ τότε αφού η $f$ είναι γνησίως φθίνουσα είναι $f(f(0))>f(0)$ . Με Bolzano για την $g(x)=f(x)-x$ στο διάστημα $[f(0),0]$ έπεται το ζητούμενο.

σ ευχαριστω πολυ!!

Aris90 · 04-01-13

χρειαζομαι βοηθεια σε συτη την ασκηση

εστω πολυωνυμικη συναρτηση f για την οποια ισχυουν :
$f'(4)=0$ και ${(f'(x))}^{2}=f(x)$ για καθε xΕR
α) να βρεθουν ο τυπος της f
β)η εξισωση της εφαπτομενης Cf στις παρακατω περιπτωσεις:
ι)εχει συντελεστη διευθυνσης λ=-1/2
ιι)σχηματιζει με τον αξονα χ'χ γωνια 135°
ιιι)ειναι παρ/λλη στην ευθεια 2x-y+1=0
ιv) ειναι καθετη στην ευθεια 2x+y-3=0
v)ειναι παραλληλη στον αξονα x'x

sokratis lyras · 04-01-13

Αρχική Δημοσίευση από Aris90:
χρειαζομαι βοηθεια σε συτη την ασκηση

εστω πολυωνυμικη συναρτηση f για την οποια ισχυουν :
$f'(4)=0$ και ${(f'(x))}^{2}=f(x)$ για καθε xΕR
α) να βρεθουν ο τυπος της f
β)η εξισωση της εφαπτομενης Cf στις παρακατω περιπτωσεις:
ι)εχει συντελεστη διευθυνσης λ=-1/2
ιι)σχηματιζει με τον αξονα χ'χ γωνια 135°
ιιι)ειναι παρ/λλη στην ευθεια 2x-y+1=0
ιv) ειναι καθετη στην ευθεια 2x+y-3=0
v)ειναι παραλληλη στον αξονα x'x

Κάποιες υποδείξεις μόνο μιας και η άσκηση είναι απλή και βασική.
α)Αν $n$ ο βαθμός του πολυωνύμου τότε $2(n-1)=n$ ...ισότητα πολυωνύμων κλπ.
β)
ι) $f'(x_0)=\displaystyle\frac{-1}{2}$
ιι) $f'(x_0)=tan135$

Όλα ακολουθούν το ίδιο μοτίβο,προσπαθησέ την με τις παραπάνω υποδείξεις.

mary-blackrose · 04-01-13

μια βοηθεια στις παρακατω.... :confused:

1)έστω η παραγωγίσιμη συνάρτηση $f:R\rightarrow R$ για τν οποία ισχύουν $\lim_{x\rightarrow -\propto }=-\propto,\lim_{x\rightarrow +\propto }=+\propto,f'(0)=\frac{1}{3},f'(x)=\frac{1}{2+e^{f(x)}}$ για καθε $x\in R$
α) Να αποδείξετε ότι η συνάρτηση $f$
i)είναι γνησίως αύξουσα στο R και να βρείτε το σύνολο τιμών της
ii)είναι κοίλη
iii)έχει μοναδική ρίζα τη χ=0
β)να αποδείξετε ότι:
i)ισχυει $e^{f(x)}+2f(x)=x+1$ για καθε $x\in R$
ii)η f αντιστρέφεται και να βρείτε τον τύπο της $f^{-1}$
iii)αν $\lambda_{1}\lambda _{2}$ οι συντελεστές διεύθυνσης των εφαπτομένων των $Cf,Cf^{-1}$ αντίστοιχα στην αρχή των αξόνων ,τότε $\lambda_{1}\lambda _{2}=1$
γ)να βρείτε την πλάγια ασύμπτωτη της $Cf$ στο $-\propto$ και στο $+\propto$

2)δίνεται η συνάρτηση $f(x)=ln\frac{e^{x}-1}{x}$
α)να βρείτε το πεδίο ορισμού της $f$
β)να δείξετε ότι για κάθε $x\in A$ ισχύει $f(x)=x+f(-x)$
γ)να βρείτε τα όρια $\lim _{x\rightarrow -\propto }f(x),\lim _{x\rightarrow \ 0 }f(x),\lim _{x\rightarrow +\propto }f(x)$
δ)να μελετήσετε την $f$ ως προς τη μονοτονία και τα ακρότατα
ε)να βρείτε το σύνολο τιμών της $f$
στ)να εξετασετε αν η $f$ είναι $\ll 1-1\gg$
ζ)να εξετάσετε αν υπάρχει εφαπτομένη της $Cf$ παράλληλη στην ευθεία $y=x+1$

Aris90 · 04-01-13

Αρχική Δημοσίευση από sokratis lyras:
Κάποιες υποδείξεις μόνο μιας και η άσκηση είναι απλή και βασική.
α)Αν $n$ ο βαθμός του πολυωνύμου τότε $2(n-1)=n$ ...ισότητα πολυωνύμων κλπ.
β)
ι) $f'(x_0)=\displaystyle\frac{-1}{2}$
ιι) $f'(x_0)=tan135$

Όλα ακολουθούν το ίδιο μοτίβο,προσπαθησέ την με τις παραπάνω υποδείξεις.

ενταξει το β το καταλαβα πανευκολο τελικα
το α δεν μπορω να καταλαβω

rebel · 5 Ιανουαρίου 2013

Αρχική Δημοσίευση από vivianouz:
2)δίνονται οι μιγαδικοί αριθμοί $z=1+i\alpha ^{x},w=x+1+i$ και η συνάρτηση $f(x)=|z|^{2}x+|w-1|^{2}$ με $x\in R$ και $\alpha >0$ .Αν ισχύει $|z-\bar{w}|\leq |\bar{z}+w|$ , τότε:
α)να δείξετε ότι $\alpha =e$
β)να βρείτε τα $\lim x_{\rightarrow -\propto } , \lim x_{\rightarrow +\propto }$
γ)να δείξετε ότι η $Cf$ δεν έχει ασύμπτωτες
δ)να δείξετε ότι η εξίσωση $f(x)=0$ είναι αδύνατη στο $R$

Εν συντομία
α) $|z-\bar{w}|\leq |\bar{z}+w| \Rightarrow |z-\bar{w}|^2 \leq |\bar{z}+w|^2 \Rightarrow zw+\overline{zw} \geq 0 \Rightarrow x+1-a^x \geq 0$
και με Fermat για την $g(x)=x+1-a^x$ προκύπτει το ζητούμενο.
β)
Βρίσκω
$f(x)=\left(1+e^{2x}\right)x+x^2+1=x^2 \left(\frac{1}{x}+\frac{e^{2x}}{x}+1+\frac{1}{x^2}\right)$
και προφανώς $\lim_{x \to -\infty}f(x)=\lim_{x \to +\infty}f(x)=+\infty$
γ) Η f είναι συνεχής σε όλο το $\mathbb{R}$ άρα δεν έχει κατακόρυφες ασύμπτωτες και επιπλέον
$\frac{f(x)}{x}=1+e^{2x}+x+\frac{1}{x}=x \left(\frac{1}{x}+\frac{e^{2x}}{x}+1+\frac{1}{x^2}\right)$
οπότε
$\lim_{ x \to +\infty}\frac{f(x)}{x}=+\infty,\,\,\,\,\lim_{ x \to -\infty}\frac{f(x)}{x}=-\infty$
άρα η f δεν έχει ούτε πλάγιες ασύμπτωτες.
δ)
Είναι $f(x)=xe^{2x}+x^2+x+1$
Η συνάρτηση $h(x)=xe^{2x}$ , λόγω μονοτονίας ( πίνακας μονοτονίας ) παρουσιάζει ελάχιστο για $x=-1/2$ το $-1/2e$
Επειδή όμως $e>2$ είναι $-1/2e>-1/4 ,\,\,(1)$
Επίσης
$x^2+x+1=\left(x+\frac{1}{2}\right)^2+\frac{3}{4} \geq \frac{3}{4},\,\,(2)$
Λόγω (1) και (2) έχουμε
$f(x) \geq \frac{3}{4}-\frac{1}{4}=\frac{1}{2}>0,\,\,\forall x \in \mathbb{R}$
και το ζητούμενο αποδείχθηκε.

sokratis lyras · 04-01-13

Αρχική Δημοσίευση από Aris90:
ενταξει το β το καταλαβα πανευκολο τελικα
το α δεν μπορω να καταλαβω

Το ζητούμενο πολυώνυμο είναι της μορφής $a_nx^n+...+a_0$ .
Ο βαθμός του παραπάνω πολυωνύμου είναι προφανώς n.Ο βαθμός της παραγώγου ενός πολυωνύμου είναι ένας κάτω,δηλαδή ο βαθμός του $f'(x)$ είναι $n-1$ .
H δοσμένη σχέση τώρα λέει ότι τα πολυώνυμα $f(x)$ και $[f'(x)]^2$ είναι ίσα και άρα έχουν ίσους βαθμούς.
Ο βαθμός του f είναι έστω n και ο βαθμός του [f'(x)]^2 είναι 2(n-1).Άρα $2n-2=n\Rightarrow n=2$ .

vivianouz · 05-01-13

Αρχική Δημοσίευση από vivianouz:
σ ευχαριστω πολυ!!

Αρχική Δημοσίευση από styt_geia:
α) Αν ήταν $f(a)=f(b)$ τότε από Rolle θα υπήρχε $\xi \in (a,b):f'(\xi)=0$ , άτοπο απ' την υπόθεση.
β) Χωρίς βλάβη της γενικότητας υποθέτουμε ότι $f(a)<f(b)$ ( εντελώς όμοια βγαίνει και για $f(a)>f(b)$ ). Εύκολα επαληθεύεται ότι
$f(a)<\frac{3f(a)+4f(b)}{7}<f(b)$
και αφού η f είναι συνεχής στο [a,b], από το θεώρημα ενδιαμέσων τιμών θα υπάρχει
$x_0 \in (a,b):f(x_0)=\frac{3f(a)+4f(b)}{7}$
γ) Προφανές από Θ.Μ.Τ. στα διαστήματα $[a,x_0],\,\,[x_0,b]$

δ) Αν $f(0)=0$ το ζητούμενο είναι προφανές.
Αν $f(0)>0$ τότε αφού η $f$ είναι γνησίως φθίνουσα είναι $f(f(0))<f(0)$ . Με Bolzano για την $g(x)=f(x)-x$ στο διάστημα $[0,f(0)]$ έπεται το ζητούμενο.
Αν $f(0)<0$ τότε αφού η $f$ είναι γνησίως φθίνουσα είναι $f(f(0))>f(0)$ . Με Bolzano για την $g(x)=f(x)-x$ στο διάστημα $[f(0),0]$ έπεται το ζητούμενο.

μηπως σου ειναι ευκολο να μου εξηγησεις λιγο το β ερωτημα...??τωρα που το ξαναειδα κολλησα....

lowbaper92 · 05-01-13

Αρχική Δημοσίευση από vivianouz:
1)έστω η παραγωγίσιμη συνάρτηση στο [α,β] με $f'(x)\neq 0$ για κάθε $x\in [\alpha ,\beta ]$
να δείξετε ότι:
α) $f(\alpha )\neq f(\beta )$
β)υπάρχει $x_{0}\in (\alpha ,\beta )$ τέτοιο ώστε $7f(x_{0})=3f(\alpha )+4f(\beta )$
γ)υπαρχουν $x_{1}\in (\alpha ,x_{0})$ και $x_{2}\in (x_{0},\beta )$ τέτοια ώστε $f'(x_{1})\cdot f'(x_{2})>0$
δ)αν για την $f:R\rightarrow R$ ισχύει επιπλέον ότι $f'(x)<0$ για κάθε $x\in R$ ,να δείξετε ότι η εξίσωση $f(x)=x$ έχει τουλάχιστον μια λύση στο $R$

Αρχική Δημοσίευση από vivianouz:
μηπως σου ειναι ευκολο να μου εξηγησεις λιγο το β ερωτημα...??τωρα που το ξαναειδα κολλησα....

Βγαίνει πάντως εύκολα και με Bolzano:

Στο 1ο ερώτημα δείξαμε ότι f(α) διάφορο του f(β). Θεωρούμε χωρίς βλάβη της γενικότητας, όπως είπε και ο Κώστας, ότι f(α)>f(β).

Έστω $g\left(x \right)=7f\left(x \right)-3f\left(\alpha \right)-4f\left(\beta \right),\; x\in \left[\alpha ,\beta \right]$

$\bullet \, g\left(\alpha \right)=7f\left(\alpha \right)-3f\left(\alpha \right)-4f\left(\beta \right)=4\left(f\left(\alpha \right) -f\left(\beta \right)\right)>0$
$\bullet \, g\left(\beta \right)=7f\left(\beta \right)-3f\left(\alpha \right)-4f\left(\beta \right)=3\left(f\left(\beta \right) -f\left(\alpha \right)\right)<0$
Άρα $g\left(\alpha \right)\cdot g\left(\beta \right)<0$

Συνεπώς, από Bolzano στο [α.β] υπάρχει ${x}_{0}\in \left(\alpha ,\beta \right):\; g\left({x}_{0} \right)=0\Leftrightarrow 7f\left({x}_{0} \right)=3f\left(\alpha \right)+4f\left(\beta \right)$

Civilara · 5 Ιανουαρίου 2013

Αρχική Δημοσίευση από mary-blackrose:
2)δίνεται η συνάρτηση $f(x)=ln\frac{e^{x}-1}{x}$
α)να βρείτε το πεδίο ορισμού της $f$
β)να δείξετε ότι για κάθε $x\in A$ ισχύει $f(x)=x+f(-x)$
γ)να βρείτε τα όρια $\lim _{x\rightarrow -\propto }f(x),\lim _{x\rightarrow \ 0 }f(x),\lim _{x\rightarrow +\propto }f(x)$
δ)να μελετήσετε την $f$ ως προς τη μονοτονία και τα ακρότατα
ε)να βρείτε το σύνολο τιμών της $f$
στ)να εξετασετε αν η $f$ είναι $\ll 1-1\gg$
ζ)να εξετάσετε αν υπάρχει εφαπτομένη της $Cf$ παράλληλη στην ευθεία $y=x+1$

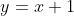
α) Για να ορίζεται η f πρέπει να ισχύει ((e^x)-1)/x>0 και x διάφορο 0.

Για x<0 έχουμε:
x<0 => e^x<1 => (e^x)-1<0
Επειδή για x<0 είναι (e^x)-1<0 τότε ισχύει x((e^x)-1)>0 και ((e^x)-1)/x>0

Για x>0 έχουμε:
x>0 => e^x>1 => (e^x)-1>0
Επειδή για x>0 είναι (e^x)-1>0 τότε ισχύει x((e^x)-1)>0 και ((e^x)-1)/x>0

Επομένως για x διάφορο ισχύει x((e^x)-1)>0 και ((e^x)-1)/x>0. Συνεπώς το πεδίο ορισμού της f είναι το A=R*

β) Για κάθε x ανήκει R* έχουμε

f(-x)=ln(((e^(-x))-1)/(-x))=ln((1-(e^(-x)))/x)=ln(((e^x)-1)/(x(e^x)))=ln[(((e^x)-1)/x)*(e^(-x))]=ln(((e^x)-1)/x)+ln(e^(-x))=
=ln(((e^x)-1)/x)+(-x)lne=f(x)-x*1=f(x)-x

Άρα για κάθε x ανήκει R* ισχύει f(-x)=f(x)-x <=> f(x)=x+f(-x)

γ) Θεωρούμε την συνάρτηση F(x)=e^x. Η F είναι συνεχής και παραγωγίσιμη στο R με πρώτη παράγωγο F΄(x)=e^x. Για x=0 έχουμε F(0)=F΄(0)=1. Από τον ορισμό της παραγώγου έχουμε:

lim(x->0)((F(x)-F(0))/(x-0))=F΄(0) <=> lim(x->0)(((e^x)-1)/x)=1

Θεωρούμε τον μετασχηματισμό u=((e^x)-1)/x. Ισχύει u>0 για κάθε x ανήκει R*. Έχουμε:

lim(x->0)f(x)=lim(x->0)ln(((e^x)-1)/x)=lim(u->1)lnu=ln1=0

lim(x->-oo)((e^x)-1)=lim(x->-oo)(e^x)+lim(x->-oo)(-1)=0+(-1)=-1
lim(x->-oo)(1/x)=0
Επομένως lim(x->-oo)(((e^x)-1)/x=[lim(x->-oo)((e^x)-1)]*[lim(x->-oo)(1/x)]=(-1)*0=0
Συνεπώς lim(x->-oo)f(x)=lim(x->-oo)ln(((e^x)-1)/x)=lim(u->0+)lnu=-oo

Θεωρούμε τις συναρτήσεις f1(x)=(e^x)+1 και f2(x)=x με πεδίο ορισμού το R. Οι συναρτήσεις f1 και f2 είναι συνεχείς και παραγωγίσιμες στο R με πρώτες παραγώγους:

f1΄(x)=e^x
f2΄(x)=1

Υπολογίζουμε το όριο lim(x->+oo)(f1΄(x)/f2΄(x)). Έχουμε:

lim(x->+oo)(f1΄(x)/f2΄(x))=lim(x->+oo)(e^x)=+oo

Επειδή lim(x->+oo)(e^x)=+oo τότε lim(x->+oo)f1(x)=lim(x->+oo)((e^x)+1)=+oo. Επίσης lim(x->+oo)f2(x)=lim(x->+oo)x=+oo.
Επειδή lim(x->+oo)f1(x)=lim(x->+oo)f2(x)=+oo τότε το όριο lim(x->+oo)(f1(x)/f2(x)) οδηγεί σε απροσδιόριστη μορφή (+oo)/(+oo). Επομένως σύμφωνα με τον κανόνα De L' Hospital έχουμε:

lim(x->+oo)(f1(x)/f2(x))=lim(x->+oo)(f1΄(x)/f2΄(x))=+oo
Άρα lim(x->+oo)(((e^x)-1)/x)=+oo

Επομένως lim(x->+oo)f(x)=lim(x->+oo)ln(((e^x)-1)/x)=lim(u->+oo)lnu=+oo

δ),ε) Θεωρούμε την συνάρτηση g με τύπο g(x)=(x-1)(e^x)+1, x ανήκει R. Η g είναι συνεχής και παραγωγίσιμη στο R με πρώτη παράγωγο:
g΄(x)=x(e^x), x ανήκει R

Για x=0 έχουμε g(0)=0

Η g είναι συνεχής στο (-oo,0], παραγωγίσιμη στο (-οο,0) και ισχύει g΄(x)<0 για κάθε x ανήκει (-οο,0). Επομένως η g είναι γνησίως φθίνουσα στο (-οο,0]. Η g είναι συνεχής στο [0,+οο), παραγωγίσιμη στο (0,+οο) και ισχύει g΄(x)>0 για κάθε x ανήκει (0,+οο). Επομένως η g είναι γνησίως αύξουσα στο [0,+οο).

x<0 => g(x)>g(0) (g γνησίως φθίνουσα) => g(x)>0
x>0 => g(x)>g(0) (g γνησίως αύξουσα) => g(x)>0

Επομένως για κάθε x ανήκει R* ισχύει g(x)>0

Η f είναι συνεχής και παραγωγίσιμη στο R* με πρώτη παράγωγο

f΄(x)=((x-1)(e^x)+1)/(x((e^x)-1))=g(x)/(x((e^x)-1)), x ανήκει R*
Ισχύει f΄(x)>0 για κάθε x στο R*

Η f είναι συνεχής στο και παραγωγίσιμη στο (-oo,0) και ισχύει f΄(x)>0 για κάθε x ανήκει (-οο,0). Επομένως η f είναι γνησίως αύξουσα στο (-oo,0). Η f είναι συνεχής στο και παραγωγίσιμη στο (0,+οο) και ισχύει f΄(x)>0 για κάθε x ανήκει (0,+οο). Επομένως η f είναι γνησίως αύξουσα στο (0,+οο).

lim(x->0)f(x)=0 <=> lim(x->0-)f(x)=lim(x->0+)f(x)=0

Επειδή η f είναι συνεχής και γνησίως αύξουσα στο (-οο,0) τότε η εικόνα του (-οο,0) είναι το διάστημα:
f((-oo,0))=(lim(x->-oo)f(x),lim(x->0-)f(x))=(-oo,0)

Επειδή η f είναι συνεχής και γνησίως αύξουσα στο (0,+oo) τότε η εικόνα του (0,+oo) είναι το διάστημα:
f((0,+oo))=(lim(x->0+)f(x),lim(x->+oo)f(x))=(0,+oo)

Το πεδίο τιμών της f είναι το εξής σύνολο:
f(A)=(-oo,0)U(0,+oo)=R*

Έχει βρεθεί ότι η f είναι γνησίως αύξουσα στα διαστήματα (-οο,0) και (0,+οο). Άρα:
i) Για δύο οποιαδήποτε x1,x2 με x1<x2<0 ισχύει f(x1)<f(x2)<0
ii) Για δύο οποιαδήποτε x1,x2 με 0<x1<x2 ισχύει 0<f(x1)<f(x2)

Για δύο οποιαδήποτε x1,x2 με x1<0<x2 ισχύει f(x1)<0<f(x2).

Επομένως για κάθε x1,x2 στο R* ισχύει η συνεπαγωγή x1<x2 => f(x1)<f(x2)

Άρα η f είναι γνησίως αύξουσα στο R*.

Όπως φαίνεται από τη μονοτονία και το πεδίο τιμών της η f δεν έχει ακρότατα.

στ) Εφόσον η f είναι γνησίως αύξουσα στο R* τότε είναι και 1-1.

ζ) Θεωρούμε την συνάρτηση h(x)=(e^x)-x, x ανήκει R. Η h είναι συνεχής και παραγωγίσιμη στο R με πρώτη παράγωγο h΄(x)+(e^x)-1. Έχουμε h(0)=1

Η h είναι συνεχής στο (-οο,0], παραγωγίσιμη στο (-οο,0) και ισχύει h΄(x)<0 για κάθε x ανήκει (-oo,0). Επομένως η h είναι γνησίως φθίνουσα στο (-οο,0]. Η h είναι συνεχής στο [0,+oo), παραγωγίσιμη στο (0,+oo) και ισχύει h΄(x)>0 για κάθε x ανήκει (0,+oo). Επομένως η h είναι γνησίως αύξουσα στο [0,+oo).

x<0 => h(x)>h(0) (h γνησίως φθίνουσα) => h(x)>1
x>0 => h(x)>h(0) (h γνησίως αύξουσα) => h(x)>1

Επομένως για κάθε x ανήκει R* ισχύει h(x)>1. Συνεπώς προκύπτει για κάθε x ανήκει R*:

h(x)>1 <=> (e^x)-x>1 <=> -(e^x)+1<-x <=> x(e^x)-(e^x)+1<x(e^x)-x <=> (x-1)(e^x)+1<x((e^x)-1) <=> ((x-1)(e^x)+1)/(x((e^x)-1))<1 <=>
<=> f΄(x)<1 για κάθε x στο R* εφόσον x((e^x)-1)>0 για κάθε x ανήκει R*.

Άρα f΄(x) διάφορο 1 για κάθε x στο R*

Επομένως δεν υπάρχει σε κανένα σημείο της Cf εφαπτομένη που να είναι παράλληλη στην ευθεία με εξίσωση y=x+1

Civilara · 5 Ιανουαρίου 2013

Αρχική Δημοσίευση από mary-blackrose:
1)έστω η παραγωγίσιμη συνάρτηση $f:R\rightarrow R$ για τν οποία ισχύουν $\lim_{x\rightarrow -\propto }=-\propto,\lim_{x\rightarrow +\propto }=+\propto,f'(0)=\frac{1}{3},f'(x)=\frac{1}{2+e^{f(x)}}$ για καθε $x\in R$
α) Να αποδείξετε ότι η συνάρτηση $f$
i)είναι γνησίως αύξουσα στο R και να βρείτε το σύνολο τιμών της
ii)είναι κοίλη
iii)έχει μοναδική ρίζα τη χ=0
β)να αποδείξετε ότι:
i)ισχυει $e^{f(x)}+2f(x)=x+1$ για καθε $x\in R$
ii)η f αντιστρέφεται και να βρείτε τον τύπο της $f^{-1}$
iii)αν $\lambda_{1}\lambda _{2}$ οι συντελεστές διεύθυνσης των εφαπτομένων των $Cf,Cf^{-1}$ αντίστοιχα στην αρχή των αξόνων ,τότε $\lambda_{1}\lambda _{2}=1$
γ)να βρείτε την πλάγια ασύμπτωτη της $Cf$ στο $-\propto$ και στο $+\propto$

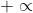
α) Η f έχει πεδίο ορισμού το A=R
i) Επειδή η f είναι παραγωγίσιμη στο R τότε είναι συνεχής στο R. Για κάθε x ανήκει R ισχύει f΄(x)=1/(2+(e^f(x)))>0 για κάθε x ανήκει R.
Η συνάρτηση f είναι συνεχής και παραγωγίσιμη στο R και ισχύει f΄(x)>0 για κάθε x ανήκει R. Άρα η f είναι γνησίως αύξουσα στο R.

ii) Επειδή η f είναι παραγωγίσιμη στο R τότε και η πρώτ η παράγωγος f΄ είναι παραγωγίσιμη στο R. Άρα η f είναι δύο φορές παραγωγίσιμη στο R με δεύτερη παράγωγο:

f΄΄(x)=(f΄(x))΄=(1/(2+(e^f(x))))΄=-[(e^f(x))/(2+(e^f(x)))]f΄(x)=-[(e^f(x))/((2+(e^f(x)))^3)]<0 για κάθε x ανήκει R

Η f είναι συνεχής και δύο φορές παραγωγίσιμη στο R και ισχύει f΄΄(x)<0 για κάθε x ανήκει R. Επομένως η f είναι κοίλη στο R που σημαίνει ότι η f΄ είναι γνησίως φθίνουσα στο R.

iii) Για x=0 έχουμε f΄(0)=1/(2+(e^f(0))). Επειδή f΄(0)=1/3 τότε έχουμε

1/(2+(e^f(0)))=1/3 <=> 2+(e^f(0))=3 <=> e^f(0)=1 <=> e^f(0)=e^0 <=> f(0)=0

Επειδή η f είναι γνησίως αύξουσα στο R τότε είναι και 1-1. Επομένως το x0=0 είναι μοναδική ρίζα της εξίσωσης f(x)=0 αφού

f(x)=0 <=> f(x)=f(0) <=> x=0 εφόσον η f είναι 1-1

β)
i) Θεωρούμε την συνάρτηση g με τύπο g(x)=(e^f(x))+2f(x)-x, x ανήκει R. Επειδή η f είναι συνεχής και παραγωγίσιμη στο R τότε και η g είναι συνεχής και παραγωγίσιμη στο R με πρώτη παράγωγο:

g΄(x)=(e^f(x))f΄(x)+2f΄(x)-1=(2+(e^f(x)))f΄(x)-1=(2+(e^f(x)))*[1/(2+(e^f(x)))]-1=1-1=0

Η g είναι συνεχής και παραγωγίσιμη στο R και ισχύει g΄(x)=0 για κάθε x ανήκει R. Επομένως υπάρχει πραγματική σταθερά c τέτοια ώστε g(x)=c για κάθε x ανήκει R.

Για x=0 έχουμε g(0)=(e^f(0))+2f(0)=(e^0)+2*0=1+0=1 και g(0)=c. Επομένως c=1 και ισχύει g(x)=1 για κάθε x ανήκει R. Άρα

g(x)=1 <=> (e^f(x))+2f(x)-x=1 <=> (e^f(x))+2f(x)=x+1 για κάθε x ανήκει R

ii) Η f είναι 1-1 άρα και αντιστρέψιμη. Θα προσδιοριστεί το πεδίο τιμών της το οποίο είναι το πεδίο ορισμού της f-1.

H f είναι συνεχής και γνησίως αύξουσα στο R, οπότε
f(A)=f(R)=(lim(x->-oo)f(x),lim(x->+oo)f(x))=(-oo,+oo)=R

Επομένως ισχύει η ισοδυναμία
y=f(x) <=> x=(f-1)(y), x ανήκει A=R, y ανήκει f(A)=R

Έχουμε:

(e^f(x))+2f(x)=x+1 <=> (e^y)+2y=x+1 <=> x=(e^y)+2y-1 <=> (f-1)(y)=(e^y)+2y-1

Άρα (f-1)(y)=(e^y)+2y-1, y ανήκει f(A)=R

έχουμε f(0)=0 <=> (f-1)(0)=0

που επαληθεύεται αφού για y=0 παίρνουμε (f-1)(0)=(e^0)+2*0-1=1+0-1=0

iii) Η f-1 είναι συνεχής και παραγωγίσιμη στο R με πρώτη παράγωγο

(f-1)΄(y)=(e^y)+2, y ανήκει R

Για y=0 έχουμε (f-1)΄(0)=(e^0)+2=1+2=3

Με γνωστή την παράγωγο της αντίστροφης συνάρτησης (f-1)΄(y), η παράγωγος της συνάρτησης f προσδιορίζεται από τον τύπο

f΄(x)=1/(f-1)΄(f(x)), x ανήκει A=R ή
f΄((f-1)(y))=1/(f-1)΄(y), y ανήκει f(A)=R

Επομένως από τον δεύτερο τύπο για y=0 προκύπτει

f΄((f-1)(0))=1/(f-1)΄(0) <=> f΄(0)=1/3

Επομένως λ1=f΄(0)=1/3 και λ2=(f-1)΄(0)=3. Συνεπώς λ1*λ2=(1/3)*3=1

γ) Θεωρούμε την συνάρτηση h(x)=x, x ανήκει R. Η h είναι συνεχής και παραγωγίσιμη στο R με πρώτη παράγωγο h΄(x)=1
Θεωρούμε τον μετασχηματισμό y=f(x). Επειδή lim(x->+oo)f(x)=+oo τότε lim(x->+oo)(e^f(x))=lim(y->+oo)(e^y)=+oo και επομένως
lim(y->+oo)(2+(e^y))=+oo. Επειδή lim(y->+oo)(2+(e^y))=+oo τότε lim(y->+oo)(1/(2+(e^y)))=0. Έχουμε:

lim(x->+oo)f΄(x)=lim(x->+oo)(1/(2+(e^f(x))))=lim(y->+oo)(1/(2+(e^y)))=0
lim(x->+oo)(f(x)-0*x)=lim(x->+oo)f(x)=+oo
Άρα η Cf δεν έχει πλάγια ασύμπτωτη στο +οο

Υπολογίζουμε το όριο lim(x->-oo)(f΄(x)/h΄(x)). Λαμβάνοντας υπόψη ότι lim(x->-oo)f(x)=-oo έχουμε

lim(x->-oo)(f΄(x)/h΄(x))=lim(x->-oo)(f΄(x)/1)=lim(x->-oo)f΄(x)=lim(x->-oo)(1/(2+(e^f(x))))=lim(y->-oo)(1/(2+(e^y)))=1/(2+0)=1/2

lim(x->-oo)(f(x)-(x/2))=lim(y->-oo)[y-((f-1)(y)/2)]=lim(y->-oo)[y-(((e^y)+2y-1)/2)]=lim(y->-oo)[(1-(e^y))/2]=(1-0)/2=1/2

Επομένως η ευθεία y=(1/2)x+(1/2) είναι ασύμπτωτη της Cf στο -οο.

Βοήθεια/Aπορίες στα Μαθηματικά Προσανατολισμού

Εκκολαπτόμενο μέλος

Νεοφερμένος

Εκκολαπτόμενο μέλος

Νεοφερμένος

Πολύ δραστήριο μέλος

Νεοφερμένος

Εκκολαπτόμενο μέλος

Πολύ δραστήριο μέλος

Πολύ δραστήριο μέλος

Νεοφερμένος

Εκκολαπτόμενο μέλος

Νεοφερμένος

Εκκολαπτόμενο μέλος

Εκκολαπτόμενο μέλος

Πολύ δραστήριο μέλος

Νεοφερμένος

Νεοφερμένος

Πολύ δραστήριο μέλος

Περιβόητο μέλος

Περιβόητο μέλος