Βοήθεια/Aπορίες στα Μαθηματικά Προσανατολισμού

[Guest 278211]

Γενικα τΟ ΚΡΙΤΗΡΙΟ Παρεμβολης ισχυει και όταν τα όρια τεινουν στο απειρο;; ή οταν το αποτελεσμα ειναι απειρο;;
Γιατι εχω μπερδευτει.Στο σχολικο λεει χ->χο αλλα σε κατι ασκησεις στο σχολειο το εχουμε χρησιμοποιησει.

1)Δηλαδη αν γ(χ)<φ(χ)<η(χ)
και πρεπει να βρεις το limφ(χ) (χ->απειρο ) γινεται να χρησιμοποιηθει το κριτηριο παρεμβολης;;


2)Α και κατι ακομα ασχετο. Αν μια συναρτηση g ειναι παραγωγισιμη και κοιλη γίνεται να πουμε ότι g' γνισιως φθινουσα;;;

1) Το κριτήριο παρεμβολής δεν έχει νόημα στο άπειρο, αν και πολλά βιβλία το γράφουν. Αν πχ f(x)>g(x) και lim g(x)=+oo για x-->+oo τότε
lim f(x)=+oo για x-->+oo
Αυτό καλό είναι να το αποδείξεις (στο φροντιστήριο ο καθηγητής λέει να το αποδείξουμε αν έχουμε χρόνο, στο σχολείο λέει πως δε χρειάζεται), χρησιμοποιώντας το κριτήριο παρεμβολής για το +οο στην ανισότητα: 0<1/f(x)<1/g(x) όπου βγαίνει lim 1/f(x)=0 (+) άρα
lim f(x)=+oo για x-->+oo

2) φυσικά

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[κωσ]

1) Το κριτήριο παρεμβολής δεν έχει νόημα στο άπειρο, αν και πολλά βιβλία το γράφουν. Αν πχ f(x)>g(x) και lim g(x)=+oo για x-->+oo τότε
lim f(x)=+oo για x-->+oo
Αυτό καλό είναι να το αποδείξεις (στο φροντιστήριο ο καθηγητής λέει να το αποδείξουμε αν έχουμε χρόνο, στο σχολείο λέει πως δε χρειάζεται), χρησιμοποιώντας το κριτήριο παρεμβολής για το +οο στην ανισότητα: 0<1/f(x)<1/g(x) όπου βγαίνει lim 1/f(x)=0 (+) άρα
lim f(x)=+oo για x-->+oo

2) φυσικά

Νομιζω οτι δεν το αναφερει πλεον καν στο βιβλιο αυτο.Και εμας μας το ειπε στο φροντ. αλλα πλεον δεν υπαρχει οποτε τυπικα δεν μπορεις να το χρησιμοποιησεις.


Σε αυτη την ασκηση τα ορια στο β ερωτημα πως βρισκονται τα οριο στο απειρο για να βρεθει το συνολο τιμων;; ;;

Εστω φ συνεχης [0,+απειρο)->R φ(0)=1 και 2χ<φ'(χ)<e^χ ,x>0
α.να δειξετε οτι χ²+1<φ(χ)<e^x ,x>0
b. να βρειτε συνολο τιμων της φ
και εχει και αλλα ερωτηματα μετα....

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Guest 278211]

Νομιζω οτι δεν το αναφερει πλεον καν στο βιβλιο αυτο.Και εμας μας το ειπε στο φροντ. αλλα πλεον δεν υπαρχει οποτε τυπικα δεν μπορεις να το χρησιμοποιησεις.


Σε αυτη την ασκηση τα ορια στο β ερωτημα πως βρισκονται τα οριο στο απειρο για να βρεθει το συνολο τιμων;; ;;

Εστω φ συνεχης [0,+απειρο)->R φ(0)=1 και 2χ<φ'(χ)<e^χ ,x>0
α.να δειξετε οτι χ²+1<φ(χ)<e^x ,x>0
b. να βρειτε συνολο τιμων της φ
και εχει και αλλα ερωτηματα μετα....

η φ είναι γν αύξουσα στο [0,+οο) από την υπόθεση (...) άρα φ(A)=[φ(0),lim...)=[1,lim...)
0<χ²+1<φ(χ) <=> 0<1/φ(χ)<1/(χ²+1)
από το κριτήριο παρεμβολής: lim 1/φ(χ) = 0 (+) άρα lim φ(χ) = +οο για χ-->+οο
φ(Α) = [1,+οο)

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[κωσ]

η φ είναι γν αύξουσα στο [0,+οο) από την υπόθεση (...) άρα φ(A)=[φ(0),lim...)=[1,lim...)
0<χ²+1<φ(χ) <=> 0<1/φ(χ)<1/(χ²+1)
από το κριτήριο παρεμβολής: lim 1/φ(χ) = 0 (+) άρα lim φ(χ) = +οο για χ-->+οο
φ(Α) = [1,+οο)

Ναι αλλα το κριτηριο παρεμβολης ισχυει μονο οταν το χ τεινει σε ενα χο αρα αυτο που εγραψες τυπικα δεν ισχυει . Δεν καταλαβαινω ...εχω μπερδευτει ......

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[antwwwnis]

ορίστε κι ένα σχηματάκι που ξεκαθαρίζει και το νόημα της άσκησης. Η φ κινείται υποχρεωτικά μεταξύ των δυο γραμμών.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[κωσ]

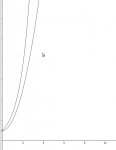
ορίστε κι ένα σχηματάκι που ξεκαθαρίζει και το νόημα της άσκησης. Η φ κινείται υποχρεωτικά μεταξύ των δυο γραμμών.

Το καταλαβαινω και το βρισκω λογικο απλα δεν καταλαβαινω πως πρεπει ν α δικαιολογησω εττοιου ειδους ορια συμφωνα με τη θεωρια του σχολικου .Γιατι δεν αναφερει τιποτα για το απειρο .....

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[antwwwnis]

Eμ, το κριτήριο παρεμβολής, αν παρατηρήσεις, δεν διευκρινίζει αν το x0 είναι πραγματικός αριθμός.
Επίσης, στο de l hospital, λέει ότι το χ0 μπορεί να είναι και άπειρο.
Οπότε δε μας εμποδίζει κανένας να θεωρήσουμε ότι το χ0 στη διατύπωση του κριτηρίου παρεμβολής μπορεί να είναι άπειρο.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[κωσ]

Eμ, το κριτήριο παρεμβολής, αν παρατηρήσεις, δεν διευκρινίζει αν το x0 είναι πραγματικός αριθμός.
Επίσης, στο de l hospital, λέει ότι το χ0 μπορεί να είναι και άπειρο.
Οπότε δε μας εμποδίζει κανένας να θεωρήσουμε ότι το χ0 στη διατύπωση του κριτηρίου παρεμβολής μπορεί να είναι άπειρο.

Ωραια οποτε το χ μπορει να τεινει το απειρο αλλα το αποτελεσμα απο τα ορια για να εφαρμοστει το κριτηριο παρεμβολης πρεπει να ειναι πραγματοκος .Ετσι;;

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[antwwwnis]

ούτε το l διευκρινίζει τι είναι

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[christina123]

εγω να ρωτησω κατι που το χω απορια:οταν μας ζηττουν να αποδειξουμε μια ανισοτητα μπορουμε να πουμε εστω οτι ισχυει και να καταληξουμε παλι σε κατι που ισχυει;;;
π.χ.www.kelafas.gr/themata.html?filename=2004/epanaliptikes/mathkat_ep_04.pdf στο θεμα 3 ερωτημα β μπορω να πω εστω οτι: f^2(β)<f^2(α)....->1<2 που ισχυει.
ειναι σωστο;;;

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Nikos Sitys]

εγω να ρωτησω κατι που το χω απορια:οταν μας ζηττουν να αποδειξουμε μια ανισοτητα μπορουμε να πουμε εστω οτι ισχυει και να καταληξουμε παλι σε κατι που ισχυει;;;
π.χ.www.kelafas.gr/themata.html?filename=2004/epanaliptikes/mathkat_ep_04.pdf στο θεμα 3 ερωτημα β μπορω να πω εστω οτι: f^2(β)<f^2(α)....->1<2 που ισχυει.
ειναι σωστο;;;

Γιατι δεν ανοιγει το url?

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[christina123]

Γιατι δεν ανοιγει το url?

καποια βλακεια θα χω κανει.
https://www.kelafas.gr/themata.html?filename=2004/epanaliptikes/mathkat_ep_04.pdf

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Nikos Sitys]

καποια βλακεια θα χω κανει.
https://www.kelafas.gr/themata.html?filename=2004/epanaliptikes/mathkat_ep_04.pdf

Eσυ βλακεια?? Αποκλειεται
Ναι ετσι θα την ελυνα και εγω.Αν και θα μου εριχνε μπατσο η καθηγητρια μου γιατι δεν της αρεσει αυτος ο τροπος τον θεωρει μπακαλιστικο αλλα δεν μπορω να αποδειξω κατι τετοιες ανισωσεις αλλιως τις περνω οπως το πηρες και εσυ

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[christina123]

Eσυ βλακεια?? Αποκλειεται
Ναι ετσι θα την ελυνα και εγω.Αν και θα μου εριχνε μπατσο η καθηγητρια μου γιατι δεν της αρεσει αυτος ο τροπος τον θεωρει μπακαλιστικο αλλα δεν μπορω να αποδειξω κατι τετοιες ανισωσεις αλλιως τις περνω οπως το πηρες και εσυ

το αντιπαρερχομαι το σχολιο...
ειναι ομως σωστο ή καποιοι μπορει να το θεωρησουν λαθος;;;

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Nikos Sitys]

το αντιπαρερχομαι το σχολιο...
ειναι ομως σωστο ή καποιοι μπορει να το θεωρησουν λαθος;;;

Σωστοτατο ειναι!Δεν ειπα πως δεν ειναι σωστο απλα σου εξηγησα τι κομπλεξικη δασκαλα εχω που το μονο που θελει ειναι να μου κανει την ζωη κολαση !!!!
τωρα αντι να λεμε απαξιω το λεμε αντιπαρερχομαι???τι κανει η εκθεση 3ης λυκειου!!

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[christina123]

Σωστοτατο ειναι!Δεν ειπα πως δεν ειναι σωστο απλα σου εξηγησα τι κομπλεξικη δασκαλα εχω που το μονο που θελει ειναι να μου κανει την ζωη κολαση !!!!
τωρα αντι να λεμε απαξιω το λεμε αντιπαρερχομαι???τι κανει η εκθεση 3ης λυκειου!!

λεκτικος πληθωρισμος
α οκ.και κατι αλλο.στο ιδιο θεμα στο α ερωτημα μπορω να παρω και εκει εστω οτι μετρο του z ειναι ισο με 1 ή στις ισοτητες δεν μπορω να το κανω;;;;

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Nikos Sitys]

λεκτικος πληθωρισμος
α οκ.και κατι αλλο.στο ιδιο θεμα στο α ερωτημα μπορω να παρω και εκει εστω οτι μετρο του z ειναι ισο με 1 ή στις ισοτητες δεν μπορω να το κανω;;;;

Μπορεις ετσι οπως το ειπες μπορεις νομιζω αν παρεις τα μετρα τους θα βγαλεις το αποτελεσμα..καταλαβες τι εννοω να υψωσεις μετρα τετραγωνα και να βγαλεις το αποτελεσμα.Ετσι οπως το ειπες ομως ειναι πιο γρηγορο!Απλα σου ειπα και μια δευτερη λυση..

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Guest 010239]

καποια βλακεια θα χω κανει.
https://www.kelafas.gr/themata.html?filename=2004/epanaliptikes/mathkat_ep_04.pdf

Γιατι δεν κανεις αντικατασταση και μετα πραξεις.Ξερεις τι ωραιο που βγαίνει; 0<2

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[SiMoS43710]

Eσυ βλακεια?? Αποκλειεται
Ναι ετσι θα την ελυνα και εγω.Αν και θα μου εριχνε μπατσο η καθηγητρια μου γιατι δεν της αρεσει αυτος ο τροπος τον θεωρει μπακαλιστικο αλλα δεν μπορω να αποδειξω κατι τετοιες ανισωσεις αλλιως τις περνω οπως το πηρες και εσυ

Αν δεν της αρέσει αυτός ο τρόπος, μπορείς να το κάνεις και με άτοπο, αρκεί να προσέχεις τι συνθήκες θα βάλεις.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[rebel]

εγω να ρωτησω κατι που το χω απορια:οταν μας ζηττουν να αποδειξουμε μια ανισοτητα μπορουμε να πουμε εστω οτι ισχυει και να καταληξουμε παλι σε κατι που ισχυει;;;
π.χ.www.kelafas.gr/themata.html?filename=2004/epanaliptikes/mathkat_ep_04.pdf στο θεμα 3 ερωτημα β μπορω να πω εστω οτι: f^2(β)<f^2(α)....->1<2 που ισχυει.
ειναι σωστο;;;

λεκτικος πληθωρισμος
α οκ.και κατι αλλο.στο ιδιο θεμα στο α ερωτημα μπορω να παρω και εκει εστω οτι μετρο του z ειναι ισο με 1 ή στις ισοτητες δεν μπορω να το κανω;;;;

Αν υποθέσεις ότι κάτι ισχύει τότε δεν έχεις τίποτα να αποδείξεις. Είναι θέμα διατύπωσης. Απλά χρησιμοποίησε την λέξη "αρκεί" ή διπλές ισοδυναμίες. Εδώ για παράδειγμα

H τελευταία ανισότητα είναι αληθής αλλά μόνο μέσω των προς τα αριστερά συνεπαγωγών ( ) μας επιτρέπεται να πούμε ότι η ζητούμενη ισχύει.

Eσυ βλακεια?? Αποκλειεται
Ναι ετσι θα την ελυνα και εγω.Αν και θα μου εριχνε μπατσο η καθηγητρια μου γιατι δεν της αρεσει αυτος ο τροπος τον θεωρει μπακαλιστικο αλλα δεν μπορω να αποδειξω κατι τετοιες ανισωσεις αλλιως τις περνω οπως το πηρες και εσυ

Καθόλου μπακαλίστικος. Αρκεί να είσαι προσεκτικός στην διατύπωση όπως ανέφερα λίγο πιο πάνω.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.