Βοήθεια/Aπορίες στα Μαθηματικά Προσανατολισμού

[red span]

συγγνωμη γραψατε 18-19 μαθηματικα??? εγω εγραψα μονο τα τρια πρωτα θεματα ολοσωστα στο τεταρτο ειχα σκεφτει καποιους αλλους τροπους λυσης αλλα δεν ειχα χρονο να τους δοκιμασω...και ενα λαθος που εκανα μου στοιχισε 13 μοναδες ουτε καν λαθος απλα δεν εσπασα τον εκθετη του e...

Θα δουμε αυριο ποσο ακριβως γραψαμε,εκτος αν εσυ τα ειδες νωριτερα

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[lowbaper92]

Απλα,τα μαθηματικα κατευθυνσης,οπως και η χημεια και η βιολογια,αμα μαθεις μεθολογιες και τα δουλεψεις σωστα,γραφεις ανετα 18-19 στο τελος.

Και άμα μπει κάτι ένα κλικ πιο έξυπνο ή συνδιαστικό θα κοιτάς το ταβάνι. Γενικά με εκνευρίζουν οι μεθοδολιγίες, γιατί θεωρώ ότι υπνωτίζουν το μυαλό και την κριτική σκέψη, καταδικάζουν εκ των προτέρων μια όμορφη εμπνευσμένη λύση και μας κάνουν να γράφουμε μηχανικά χωρίς να καταλαβαίνουμε.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[rebel]

το συνολο τιμων της f ειναι το R

αλλιώς αρκεί να δείξω ότι για κάθε η εξίσωση έχει λύση ως προς χ.

Αν η (1) έχει λύση ως προς χ τότε από την δοθείσα σχέση θα έχουμε . Βρήκαμε μια πιθανή ρίζα της (1) οπότε μένει να δούμε αν η τιμή επαληθεύει την (1). Από την δοθείσα σχέση και πάλι έχουμε

αφού

πηγή: Ευκλείδης Β' τεύχος 78 σελ 70

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[red span]

αλλιώς αρκεί να δείξω ότι για κάθε η εξίσωση έχει λύση ως προς χ.

Αν η (1) έχει λύση ως προς χ τότε από την δοθείσα σχέση θα έχουμε . Βρήκαμε μια πιθανή ρίζα της (1) οπότε μένει να δούμε αν η τιμή επαληθεύει την (1). Από την δοθείσα σχέση και πάλι έχουμε

αφού

πηγή: Ευκλείδης Β' τεύχος 78 σελ 70

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[papas]

Και άμα μπει κάτι ένα κλικ πιο έξυπνο ή συνδιαστικό θα κοιτάς το ταβάνι. Γενικά με εκνευρίζουν οι μεθοδολιγίες, γιατί θεωρώ ότι υπνωτίζουν το μυαλό και την κριτική σκέψη, καταδικάζουν εκ των προτέρων μια όμορφη εμπνευσμένη λύση και μας κάνουν να γράφουμε μηχανικά χωρίς να καταλαβαίνουμε.

Οπως,πχ φετος,το Δ3;

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[red span]

Και άμα μπει κάτι ένα κλικ πιο έξυπνο ή συνδιαστικό θα κοιτάς το ταβάνι. Γενικά με εκνευρίζουν οι μεθοδολιγίες, γιατί θεωρώ ότι υπνωτίζουν το μυαλό και την κριτική σκέψη, καταδικάζουν εκ των προτέρων μια όμορφη εμπνευσμένη λύση και μας κάνουν να γράφουμε μηχανικά χωρίς να καταλαβαίνουμε.

Χαρη δεν συμφωνο,
Οι μεθοδοι ειναι οι συνηθειες του πνευματος και οι οικονομιες της μνημης
Rivarol

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[antwwwnis]

Οι μεθοδολογιες ειναι για τα πολυ βασικα, ετσι τουλαχιστον δουλευω εγω- αναλυτικα.
Βεβαια,μεχρι το τελος της επομενης χρονιας, πιστευω πως θα εχω λυσει αρκετες ασκησεις ωστε να μην πεσει κατι που να μην εχω ξαναδει.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[lowbaper92]

Οπως,πχ φετος,το Δ3;

Όπως πχ το Δ4 και όπως πχ στο Πανεπιστήμιο που θα πας και δε θα έχεις το φροντιστή να σου γράφει μεθοδολογίες.

Χαρη δεν συμφωνο,
Οι μεθοδοι ειναι οι συνηθειες του πνευματος και οι οικονομιες της μνημης
Rivarol

Εδώ αναφερόμαστε στα Μαθηματικά. Δε νομίζω ο τύπος αυτός να είχε στο μυαλό του τα Μαθηματικά όταν το έλεγε αυτό. Για τα Μαθηματικά εγώ πιστεύω στο
"Let Solutions Say Your Method "

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[red span]

Καποια ερωτηματα που μου αρεσουν αρκετα
Α)Αν η f αρτια και η αντιστροφη ειναι αρτια
Β)Αν η f συνεχης τοτε και η αντιστροφη ειναι συνεχης
Γ)Αν η f παραγωγισιμη και f'(x)<>0 τοτε και η αντιστροφη ειναι παραγωγισιμη στο πεδιο ορισμου της συνολο τιμων το R
Δ)Αν η f κυρτη τοτε και η αντιστροφη κυρτη?
Ε)Αν η f περιοδικη τοτε και και η f' περιοδικη
Ζ)Αν η f αρτια τοτε η f' περριτη
Η)Αν η f ειναι γνησιως αυξουσα και η αντιστροφη ειναι γνησιως αυξουσα (2 τροποι)
Θ)Αν η f περριτη και γνησιως φθινουσα τοτε ισχυει η ισοδυναμια τοτε τα κοινα σημεια της f και της αντιστροφης βρισκονται πανω στην y=-x
Ι) Eστω f,g με πεδιο και συνολο τιμων το R για της οποιες ισχυει fog ειναι 1-1 τοτε και f,g ειναι 1-1 (δυσκολο ερωτημα)
Κ)Αν η f εχει ελαχσιτο και ειναι περριτη ,να αποδειξετε οτι παρουσιαζει και μεγιστο
Σε καποια ερωτημα που δεν αναφερω να παρετε σαν δεδομενο οτι f:R-->R
Oποια προσθηκη δεκτη
Φιλικα Χαρης
Y.Γ(Οπου εχω ερωτηματικο δεν ξερω αν ευσταθουν τα ερωτηματα αυτα)

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[mikri_tulubitsa]

Ρε παιδιά πώς μπορώ να βρω την μονοτονία της ?

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[tebelis13]

Ρε παιδιά πώς μπορώ να βρω την μονοτονία της ?

H f είναι παραγωγίσιμη?

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[red span]

η g(x)=x^3+2x ειναι γνησιως αυξουσα,απο την 1 εχω gof(x)=3x ,οταν δυο συναρτησεις ειναι ισες εχουν την ιδια μονοτονια δηλαδη και η gof ειναι γνησιως αυξουσα αφου η 3χ ειναι αυξουσα,Τωρα για χ1<χ2 εχω gof(x1)<gof(x2) η g γνησιως αυξουα αρα f(x1)<f(x2) γνησιως αυξουσα η f
Αν η ασκηση σε ελεγε να αποδειξης οτι ειναι γνησιως αυξουσα μπορουσες να το πας με ατοπο
εστω οτι η f δεν ειναι γνησιως αυξουσα χ1<χ2 f(x1)>=f(x2) ................................................... χ1>=χ2 ατοπο αρα η f γνησιως αυξουσα
Φιλικα Χαρης

Όπως πχ το Δ4 και όπως πχ στο Πανεπιστήμιο που θα πας και δε θα έχεις το φροντιστή να σου γράφει μεθοδολογίες.


Εδώ αναφερόμαστε στα Μαθηματικά. Δε νομίζω ο τύπος αυτός να είχε στο μυαλό του τα Μαθηματικά όταν το έλεγε αυτό. Για τα Μαθηματικά εγώ πιστεύω στο
"Let Solutions Say Your Method "

Θες να αρχισουμε να μιλαμε και για το πανεπιστημιο?
Τοτε η μαθηματικη επαγωγη ειναι απαραιτητο εργαλειο του μαθητη οχι μονο στην 3 λυκειου αλλα και στο πανεπιστημιο,κατι που εσυ το απεκλισες,οπως και οι προοδοι (αριθμητικη ,γεωμετρικη,αρμονικη),προτρεποντας τους να μην το διαβασουν
Φιλικα Χαρης

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[lowbaper92]

Θες να αρχισουμε να μιλαμε και για το πανεπιστημιο?
Τοτε η μαθηματικη επαγωγη ειναι απαραιτητο εργαλειο του μαθητη οχι μονο στην 3 λυκειου αλλα και στο πανεπιστημιο,κατι που εσυ το απεκλισες,οπως και οι προοδοι (αριθμητικη ,γεωμετρικη,αρμονικη),προτρεποντας τους να μην το διαβασουν
Φιλικα Χαρης

Μην διαστρεβλώνεις τι είπα. Η ερώτηση ήταν αν θα χρειαστούν στη Γ Λυκείου, κι εγώ απάντησα ότι δεν θα του χρειαστούν στη Γ Λυκείου.
Και υπάρχει μια βασική διαφορά αυτού που λέω εγώ και αυτού που λες εσύ. Άλλο δεν ξέρω κάποιο κεφάλαιο (αυτό άλλωστε καλύπτεται και όταν μπεις στο Πανεπιστήμιο), και άλλο έχω αναπτύξει μια λανθασμένη νοοτροπία διαβάσματος, νομίζοντας πως οτιδήποτε και να μου ζητηθεί να λύσω, θα λύνεται με "Βήμα 1ο, Βήμα 2ο κτλ" Στο Πανεπστήμιο είσαι εσύ και ο εαυτός σου στο διάβασμα. Μπορεί να χρειαστεί να διαβάσεις ολόκληρο μάθημα που δεν έχεις ξαναδεί στη ζωή σου κάτι παρόμοιο, μόνος σου, μόνο και μόνο επειδή οι παραδόσεις του καθηγητή είναι χάλια. Αν εσύ έχεις συνηθίσει μασημένη τροφή και να στα εξηγούν όλα τέλεια, θα ζοριστείς πολύ. Γι'αυτό θεωρώ ότι πρέπει να βάζουμε και λίγο το μυαλό μας να δουλεύει και να μην σκεφτόμαστε μηχανικά με μεθοδολογίες.
(το β ενικό δεν πάει σε σένα προσωπικά, γενικά μιλάω)

ΥΓ. Ναι, εφόσον η τρίτη λυκείου (υποτίθεται ότι) σε προετοιμάζει για να μπεις στο πανεπιστήμιο, πρέπει να έχουμε και αυτό στο μυαλό μας.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Civilara]

Ρε παιδιά πώς μπορώ να βρω την μονοτονία της ?

Έστω Α το πεδίο ορισμού της και f(A) το πεδίο τιμών της. Αποδεικνύεται αρχικά εύκολα ότι η f είναι 1-1. Έστω ότι x1, x2 ανήκει Α με f(x1)=f(x2). Τότε θα ισχύουν οι ισότητες (f(x1))^3=(f(x2))^3 , 2f(x1)=2f(x2).

Προσθέτωντας κατά μέλη της 2 ισότητες προκύπτει (f(x1))^3+2f(x1)=(f(x2))^3+2f(x2) => 3x1=2x2 => x1=x2

Αποδείχτηκε ότι αν f(x1)=f(x2) τότε x1=x2. Άρα η f είναι 1-1 και συνεπώς αντιστέψιμη. Επομένως για κάθε x ανήκει A και y ανήκει f(Α) ισχύει η ισοδυναμία:

y=f(x) <=> x=(f-1)(y)

(f(x))^3+2f(x)=3x => y^3+2y=3(f-1)(y) => (f-1)(y)=(1/3)y^3+(2/3)y

Η f-1 του y έχει πεδίο ορισμού το R, άρα το πεδίο τιμών της f είναι το f(A)=R. Ως πολυωνυμική συνάρτηση είναι συνεχής και παραγωγίσιμη στο R με πρώτη παράγωγο (f-1)΄(y)=y^2+(2/3)>0 για κάθε y στο R.

Η f-1 είναι συνεχής και παραγωγίσιμη στο R και ισχύει (f-1)΄(y)>0 για κάθε y ανήκει R. Άρα η f-1 είναι γνησίως αύξουσα στο R.

Επειδή η f-1 είναι συνεχής και γνησίως αύξουσα στο R και ισχύουν lim(y->-άπειρο)(f-1)(y)=-άπειρο και lim(y->+άπειρο)(f-1)(y)=+άπειρο, τότε το πεδίο τιμών της είναι (-άπειρο,+άπειρο)=R. Άρα το πεδίο ορισμού της f είναι το Α=R.

Επειδή η f-1 είναι αντιστρέψιμη και γνησίως αύξουσα στο f(A)=R τότε και η αντίστροφή της, δηλαδή η f, είναι γνησίως αύξουσα στο A=R.

Γενικά η αντίστροφη συνάρτηση μιας συνάρτησης 1-1 ακολουθεί τη μονοτονία της. Αυτό αφήνεται ως άσκηση.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[red span]

Spoiler

Έστω Α το πεδίο ορισμού της και f(A) το πεδίο τιμών της. Αποδεικνύεται αρχικά εύκολα ότι η f είναι 1-1. Έστω ότι x1, x2 ανήκει Α με f(x1)=f(x2). Τότε θα ισχύουν οι ισότητες (f(x1))^3=(f(x2))^3 , 2f(x1)=2f(x2).

Προσθέτωντας κατά μέλη της 2 ισότητες προκύπτει (f(x1))^3+2f(x1)=(f(x2))^3+2f(x2) => 3x1=2x2 => x1=x2

Αποδείχτηκε ότι αν f(x1)=f(x2) τότε x1=x2. Άρα η f είναι 1-1 και συνεπώς αντιστέψιμη. Επομένως για κάθε x ανήκει A και y ανήκει f(Α) ισχύει η ισοδυναμία:

y=f(x) <=> x=(f-1)(y)

(f(x))^3+2f(x)=3x => y^3+2y=3(f-1)(y) => (f-1)(y)=(1/3)y^3+(2/3)y

Η f-1 του y έχει πεδίο ορισμού το R, άρα το πεδίο τιμών της f είναι το f(A)=R. Ως πολυωνυμική συνάρτηση είναι συνεχής και παραγωγίσιμη στο R με πρώτη παράγωγο (f-1)΄(y)=y^2+(2/3)>0 για κάθε y στο R.

Η f-1 είναι συνεχής και παραγωγίσιμη στο R και ισχύει (f-1)΄(y)>0 για κάθε y ανήκει R. Άρα η f-1 είναι γνησίως αύξουσα στο R.

Επειδή η f-1 είναι συνεχής και γνησίως αύξουσα στο R και ισχύουν lim(y->-άπειρο)(f-1)(y)=-άπειρο και lim(y->+άπειρο)(f-1)(y)=+άπειρο, τότε το πεδίο τιμών της είναι (-άπειρο,+άπειρο)=R. Άρα το πεδίο ορισμού της f είναι το Α=R.

Επειδή η f-1 είναι αντιστρέψιμη και γνησίως αύξουσα στο f(A)=R τότε και η αντίστροφή της, δηλαδή η f, είναι γνησίως αύξουσα στο A=R.

Γενικά η αντίστροφη συνάρτηση μιας συνάρτησης 1-1 ακολουθεί τη μονοτονία της. Αυτό αφήνεται ως άσκηση.

Cilvara
1).Πως θετεις το f^-1(y) αφου δεν εχεις αποδειξη οτι η f εχει συνολο τιμων το R.Οτι η f εχει πεδιο ορισμου το R δινεται εξ αρχης.Γενικα ο τροπος που ακουλουθεις δεν ειναι λαθος αλλα θελει να αποδειξης τα παραπανω.

Μην διαστρεβλώνεις τι είπα. Η ερώτηση ήταν αν θα χρειαστούν στη Γ Λυκείου, κι εγώ απάντησα ότι δεν θα του χρειαστούν στη Γ Λυκείου.
Και υπάρχει μια βασική διαφορά αυτού που λέω εγώ και αυτού που λες εσύ. Άλλο δεν ξέρω κάποιο κεφάλαιο (αυτό άλλωστε καλύπτεται και όταν μπεις στο Πανεπιστήμιο), και άλλο έχω αναπτύξει μια λανθασμένη νοοτροπία διαβάσματος, νομίζοντας πως οτιδήποτε και να μου ζητηθεί να λύσω, θα λύνεται με "Βήμα 1ο, Βήμα 2ο κτλ" Στο Πανεπστήμιο είσαι εσύ και ο εαυτός σου στο διάβασμα. Μπορεί να χρειαστεί να διαβάσεις ολόκληρο μάθημα που δεν έχεις ξαναδεί στη ζωή σου κάτι παρόμοιο, μόνος σου, μόνο και μόνο επειδή οι παραδόσεις του καθηγητή είναι χάλια. Αν εσύ έχεις συνηθίσει μασημένη τροφή και να στα εξηγούν όλα τέλεια, θα ζοριστείς πολύ. Γι'αυτό θεωρώ ότι πρέπει να βάζουμε και λίγο το μυαλό μας να δουλεύει και να μην σκεφτόμαστε μηχανικά με μεθοδολογίες.
(το β ενικό δεν πάει σε σένα προσωπικά, γενικά μιλάω)

ΥΓ. Ναι, εφόσον η τρίτη λυκείου (υποτίθεται ότι) σε προετοιμάζει για να μπεις στο πανεπιστήμιο, πρέπει να έχουμε και αυτό στο μυαλό μας.

Χαρη,δεν πιστευω πως οι μεθολογιες ειναι μασημενοι τροφοι.Ας πουμε στα ολοκληρωματα αν χρειαστει να θεσεις σε ενα ριζικο π.χ ριζα(1-χ²) χρειαστει να θεσεις χ=1/ημθ.Που λες πως στο καλο θα το ξες αυτο αν δεν εχεις μελετετησει την μεθολογια για την επιλυση τετοιων παραδειγματων ??.Πιστευω οτι το παραδειγμα μου ηταν κατατοπιστικο διοτι σε μερικα πραγματα απλα δεν σε παει με τιποτα το μυαλο,απο πολυωνυμο να καταληξεις σε τριγωνομετρικο αριθμο ?

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[lowbaper92]

Χαρη,δεν πιστευω πως οι μεθολογιες ειναι μασημενοι τροφοι.Ας πουμε στα ολοκληρωματα αν χρειαστει να θεσεις σε ενα ριζικο π.χ ριζα(1-χ²) χρειαστει να θεσεις χ=1/ημθ.Που λες πως στο καλο θα το ξες αυτο αν δεν εχεις μελετετησει την μεθολογια για την επιλυση τετοιων παραδειγματων ??.Πιστευω οτι το παραδειγμα μου ηταν κατατοπιστικο διοτι σε μερικα πραγματα απλα δεν σε παει με τιποτα το μυαλο,απο πολυωνυμο να καταληξεις σε τριγωνομετρικο αριθμο ?

Ακριβώς αυτό. Ο μαθητής που διαβάζει μεθοδολογίες θα θέσει αυτό που λες (δεν ξέρω αν βγαίνει μ'αυτήν την αντικατάσταση, δεν το' χω δοκιμάσει)
Ο μαθητής που βάζει το μυαλό του να σκεφτεί θα πει "Κάτσε έχω στο υπόρριζο το . Αν είχα το θα ήταν πολύ καλύτερα γιατί θα εκμεταλλευόμουν τη βασική τριγωνομετρική ταυτότητα. Ώπα ! Ας θέσω x=συνu "
Δες άλλο ένα παράδειγμα με τέτοια τριγωνομετρική αντικατάσταση εδώ
Και εννοείται πως δεν εννοώ να μην διαβάζουμε λυμένα, αν κατάλαβες αυτό. Εννοώ να μην ανατρέχουμε στις μεθοδολογίες του φροντιστηρίου όποτε έχουμε να λύσουμε μια άσκηση, και να την λύνουμε τυφλοσούρτικα εφαρμόζοντας απλά τα βήματα που λένε.
Btw καλά αποτελέσματα για αύριο.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Civilara]

Cilvara
1).Πως θετεις το f^-1(y) αφου δεν εχεις αποδειξη οτι η f εχει συνολο τιμων το R.Οτι η f εχει πεδιο ορισμου το R δινεται εξ αρχης.Γενικα ο τροπος που ακουλουθεις δεν ειναι λαθος αλλα θελει να αποδειξης τα παραπανω.

Σωστή παρατήρηση και την περίμενα. Το πεδίο ορισμού της f θα έπρεπε να δίνεται. Είναι παράλειψη της εκφώνησης, γι αυτό και έκανα την παραδοχή ότι το πεδίο ορισμού της f είναι το ευρύτερο δυνατό για το οποίο η εξίσωση (f(x))^3+2f(x)=3x έχει μοναδική πραγματική λύση.

Θεώρησε τη συνάρτηση g(y)=y^3+2y+α όπου α πραγματικός αριθμός. Το πεδίο ορισμού της g είναι το Dg=R ως πολυωνυμικής συνάρτησης.

Η συνάρτηση g είναι συνεχής και παραγωγίσιμη στο R με παράγωγο g'(y)=3y^2+2>=2>0. Επειδή η g είναι συνεχής και παραγωγίσιμη στο R με g΄(y)>0 για κάθε y ανήκει R τότε η g είναι γνησίως αύξουσα στο R και συνεπώς 1-1 οπότε και αντιστρέψιμη.

Επειδή η g είναι συνεχής και γνησίως αύξουσα στο R με lim(y->+άπειρο)g(y)=+άπειρο και lim(y->-άπειρο)g(y)=-άπειρο τότε το πεδίο τιμών της είναι το g(Dg)=(-άπειρο,+άπειρο)=R. Επειδή το 0 ανήκει στο g(Dg) και η g είναι 1-1 τότε υπάρχει μοναδικό y0 στο R τέτοιο ώστε g(y0)=0 => y0^3+2y0=-α.

Άρα για κάθε πραγματικό αριθμό α, υπάρχει μοναδικό y τέτοιο ώστε y^3+2y=-α. Αν λοιπόν α=α(x)=-3χ όπου χ πραγματικός αριθμός τότε υπάρχει μοναδικό y=f(x) τέτοιο ώστε (f(x))^3+2f(x)=3x. Συνεπώς για κάθε πραγματικό αριθμό x υπάρχει μοναδικό πραγματικό f(x). Εφόσον λοιπόν δεν δίνεται το πεδίο ορισμού της f από την εκφώνηση, τότε γίνεται η παραδοχή ότι το πεδίο ορισμού της f είναι το ευρύτερο δυνατό σύνολο για το οποίο η εξίσωση (f(x))^3+2f(x)=3x έχει μοναδική λύση ως προς f(x).

Αν για κάποιο x η εξίσωση αυτή έδινε 2 ή 3 πραγματικές λύσεις (εξίσωση 3ου βαθμού) τότε η διαδικασία f δεν θα ήταν συνάρτηση και δεν θα είχε έννοια η άσκηση. Αν για κάποιο x αυτή η εξίσωση δεν είχε λύση, τότε το αυτό το x δεν θα ανήκε στο πεδίο ορισμού της συνάρτησης f. Στη συγκεκριμένη περίπτωση δεν συμβαίνει τίποτα από τα δύο.

--

Ισχυει
α.να δειχτει οτι η f 1-1.
β.να βρεθει η
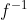
γ.να λυθει η εξισωση f(-9x+15)=x-1
Απο την 2 χρειαζομαι βοηθεια μονο στο γ.

Ισχύει (f(x))^3+2f(x)=-x για κάθε x στο πεδίο ορισμού Α της f. Επειδή το πεδίο ορισμού της f δεν δίνεται γίνεται η παραδοχή ότι είναι το σύνολο εκείνο, υποσύνολο του R, για το οποίο η εξίσωση (f(x))^3+2f(x)=-x έχει για κάθε x μοναδική πραγματική λύση ως προς f(x). Αν για κάποιο x η εξίσωση αυτή είναι αδύνατη τότε αυτό το x δεν ανήκει στο πεδίο ορισμού της f. Σε περίπτωση που για κάποιο x η εξίσωση αυτή έχει 2 ή 3 πραγματικές λύσεις τότε πάλι το x αυτό δεν ανήκει στο πεδίο ορισμού της f καθώς τότε η διαδικασία f δεν θα ήταν συνάρτηση αφού από ένα x θα προκύπτουν 2 ή 3 f(x), που είναι άτοπο.

Θεωρώ την συνάρτηση g(y)=y^3+2y+α με πεδίο ορισμού Dg=R και α πραγματικός αριθμός. Η g είναι συνεχής και παραγωγίσιμη στο R ως πολυωνυμική με g΄(y)=3y^2+2>=2>0 για κάθε πραγματικό y. Επιπλέον lim(y->-άπειρο)g(y)=-άπειρο και lim(y->+άπειρο)g(y)=+άπειρο. Επειδή η g είναι συνεχής και παραγωγίσιμη στο R με g΄(y)>0 για κάθε y ανήκει R τότε η g είναι γνησίως αύξουσα στο R. Άρα η g είναι 1-1 και συνεπώς είναι αντιστρέψιμη. Επειδή η g είναι συνεχής και γνησίως αύξουσα στο R με lim(y->-άπειρο)g(y)=-άπειρο και lim(y->+άπειρο)g(y)=+άπειρο τότε g(Dg)=(-άπειρο,+άπειρο)=R. Επειδή η g είναι 1-1 και 0 ανήκει g(Dg) τότε υπάρχει μοναδικό y0 στο R τέτοιο ώστε g(y0)=0 => y0^3+2y0+α=0.

Άρα για κάθε πραγματικό αριθμό α υπάρχει μοναδικός πραγματικός αριθμός y τέτοιος ώστε y^3+2y+α=0. Αν α=h(x)=x οπου x πραγματικός αριθμός τότε για κάθε x στο R υπάρχει μοναδικό y=f(x) τέτοιο ώστε
(f(x))^3+2f(x)+x=0

Άρα για κάθε x ανήκει R, η παραπάνω εξίσωση έχει μοναδική πραγματιή ρίζα ως προς R και συνεπώς το ευρύτερο δυνατό σύνολο για το οποίο η εξίσωση αυτή έχει ως προς f(x) μοναδική πραγματική ρίζα είναι το R. Άρα γίνεται η παραδοχή λόγω ανεπάρκειας δεδομένων ότι το πεδίο ορισμού της f είναι το R.

α) Θεωρούνται x1,x2 ανήκουν R για τα οποία f(x1)=f(x2). Τότε θα ισχύουν (f(x1))^3=(f(x2))^3 και 2f(x1)=2f(x2). Προσθέτωντας τις δύο τελευταίες ισότητες προκύπτει (f(x1))^3+2f(x1)=(f(x2))^3+2f(x2) => -x1=-x2 => x1=x2

Αποδείχτηκε ότι για δύο οποιοαδήποτε x1, x2 στο R για τα οποία f(x1)=f(x2) τότε x1=x2. Άρα η f είναι 1-1 και συνεπώς αντιστρέψιμη.

β) Η h(x)=x έχει πεδίο οριμσού και πεδίο τιμών το R, οπότε το α κινεσε όλο το R για τα διάφορα x. Επειδή η g παραπάνω έχει πεδίο ορισμού και πεδίο τιμών το R τότε για κάθε x στο R το y ανήκει στο R έτσι ώστε οι τιμές του y για τα διάφορα x να καταλαμβάνουν όλο το R και όχι κάποιο γνήσιο υποσύνολό του. Αυτό σημαίνει ότι y κινείται σε όλο το R και συνεπώς το πεδίο τιμών της f(x) είναι το R. Άρα f(A)=R εφόσον A=R.

Εφόσον η f είναι αντιστρέψιμη τότε για κάθε x στο Α=R και για κάθε y στο f(A)=R ισχύει η ισοδυναμία:
y=f(x) <=> x=(f-1)(y)

(f(x))^3+2f(x)+x=0 => y^3+2y+(f-1)(y)=0 => (f-1)(y)=-y^3-2y

γ) f(-9x+15)=x-1 <=> -9x+15=(f-1)(x-1) <=> -9x+15=-(x-1)^3-2(x-1) <=> x^3-3x^2-4x+12=0 <=>
<=> x^2(x-3)-4(x-3)=0 <=> (x-3)(x^2-4)=0 <=> (x-3)(x-2)(x+2)=0 <=> x=3 ή x=2 ή x=-2

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[red span]

Καποια ερωτηματα που μου αρεσουν αρκετα
Α)Αν η f αρτια και η αντιστροφη ειναι αρτια
Β)Αν η f συνεχης τοτε και η αντιστροφη ειναι συνεχης
Γ)Αν η f παραγωγισιμη και f'(x)<>0 τοτε και η αντιστροφη ειναι παραγωγισιμη στο πεδιο ορισμου της συνολο τιμων το R
Δ)Αν η f κυρτη τοτε και η αντιστροφη κυρτη?
Ε)Αν η f περιοδικη τοτε και και η f' περιοδικη
Ζ)Αν η f αρτια τοτε η f' περριτη
Η)Αν η f ειναι γνησιως αυξουσα και η αντιστροφη ειναι γνησιως αυξουσα (2 τροποι)
Θ)Αν η f περριτη και γνησιως φθινουσα τοτε ισχυει η ισοδυναμια τοτε τα κοινα σημεια της f και της αντιστροφης βρισκονται πανω στην y=-x
Ι) Eστω f,g με πεδιο και συνολο τιμων το R για της οποιες ισχυει fog ειναι 1-1 τοτε και f,g ειναι 1-1 (δυσκολο ερωτημα)
Κ)Αν η f εχει ελαχσιτο και ειναι περριτη ,να αποδειξετε οτι παρουσιαζει και μεγιστο
Σε καποια ερωτημα που δεν αναφερω να παρετε σαν δεδομενο οτι f:R-->R
Oποια προσθηκη δεκτη
Φιλικα Χαρης
Y.Γ(Οπου εχω ερωτηματικο δεν ξερω αν ευσταθουν τα ερωτηματα αυτα)

Δεν θελω να ξεχαστει,δειτε λιγο αν εχετε χρονο
Φιλικα Χαρης

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[rebel]

Α)Αν η f αρτια και η αντιστροφη ειναι αρτια

Θα κάνω αυτό που είναι εύκολο. Θεωρώ μία συνάρτηση με . Τότε αν θεωρήσω ένα οποιοδήποτε με θα έχω ότι και . Άρα η f δεν είναι 1-1 συνεπώς ούτε και αντιστρέψιμη.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[red span]

Α)Οπως ειπε ο Κωστας η f δεν ειναι αντιστρεψιμη.Ομως αν η f περριτη τοτε και η f^-1 ειναι περριτη.
Αποδειξη
f(f^-1(x))=x (1)
Θετω οπου χ το -χ f(f^-1(-x))=-x
λογω της 1 f(f^-1(-x))=-f(f^-1(x)
f(f^-1(x))=f(-f^-1(x))
η f ειναι ''1-1''
f^-1(x)=-f^-1(x)
Αρα η f^-1 περριτη
η f ομως περριτη αρα το μειον στο δευτερο μελος μπαινει μεσα
β)Η αποδειξη οτι αν η f ειναι συνεχης και η f^-1 ειναι συνεχης,χρειαζεται ανωτατα εργαλεια του ολοκληρωτικου λογισμου αλλα θα κανω μια προσπαθεια με την λογικη για να γινει κατανοητο
Εστω οτι εχουμε ενα σημειο Μ(χο,f(xo)) στο οποιο η f ειναι συνεχη,η f αφου ειναι αντιστρεψιμη πρεπει να ειναι συμμετρικη ως προς την y=x με την αντιστοφη της.Τωρα αν σε αυτο το σημειο η αντισρτοφη δεν ειναι συνεχης τοτε δεν υπαρχει καμια συμμετρια.
Ελπιζω με λιγα λογια να το πιασατε

Παω στο Δ γιατι το Γ απετει γνωσεις LaStex που εγω δεν γνωριζω
Δ)Εβγαλα συμπερασμα
Αν η f :R-->R ειναι κυρτη και γνησιως αυξουσα τοτε η f ειναι κοιλη
Αποδ
Η f κυρτη αρα f' ειναι γνησιως αυξουσα
χ1<χ2 =>f'(x1)<f'(x2)
f(f^-1(x))=x
Παραγωγιζοντας f'(f^-1(x))*(f^-1(x))'=1
(f^-1(x))'=1/f'(f^-1(x) (1)
Αν η f ειναι γνησιως αυξουσα τοτε και η αντιστροφη ειναι γνησιως αυξουσα
χ1<χ2=> f^-1(x1)<f ^-1(x2)
Και αφου η f' ειναι γνησιως αυξουσα συνθετοντας
f'(f^-1(x1)<f"(f^-1(x2))
1/f'(f^-1(x1)>1/f'(f^-1(x2)
και λογο της (1) εχω (f^-1(x1))'>(f^-1(x2))'
αρα η f^-1 κοιλη
Θα επανελθω με τα αλλα ερωτηματα
ΦΙλικα Χαρης

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.