rebel
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
DumeNuke
Τιμώμενο Μέλος


1. Γιατι ισχυει αυτο?
2. Πως αποδεικνυουμε την περιοδο μιας συναρτησης;
1. Γενικά, θες ένα διάστημα που η συνάρτηση σου να είναι συνεχής. Για παράδειγμα, ναι, μπορείς να μελετήσεις τη συνάρτηση f(x)=εφχ στο διάστημα [0,π] και να βγάλεις τα ίδια συμπεράσματα με το να την εξετάσεις στο διάστημα (-π/2,π/2). Η συνάρτηση είναι περιοδική, με περίοδο π, και, από την στιγμή που την εξετάζεις σε διάστημα της μορφής [(κ,κ+π)], έχεις τελειώσει.
Απλώς, είναι πιο βολικό να μην έχεις τα σημεία ασυνέχεια μέσα στο πεδίο που εξετάζεις.
Κατόπιν, από τα διαστήματα που ικανοποιούν το παραπάνω, επιλέγεις εκείνο που είναι πιο κοντά στο 0. Συνήθως, μικρότεροι αριθμοί σημαίνουν λιγότερες/ευκολότερες πράξεις.
Δεν επιβάλλει κανείς να διαλέξεις αυτό το διάστημα, απλώς είναι κάτι που συνηθίζεται.
2. Γενικά, ακολουθείς την διαδικασία που σου έδειξε ο styt, ώστε να καταλήξεις σε μια σχέση της μορφής:
f(x)=f(x+ω), όπου ω η περίοδος της συνάρτησης f.
Ειδικά για τις τριγωνομετρικές συναρτήσεις, οι περίοδοι τους θεωρούνται γνωστοί και δεδομένοι από την Τριγωνομετρία της Β' Λυκείου. Δεν χρειάζεται να αποδείξεις ότι το συνχ είναι περιοδική συνάρτηση με περίοδο 2π....
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Γατόπαρδος.
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Γατόπαρδος.
Πολύ δραστήριο μέλος


2)την εξισωση 3συνχ=-ριζα3ημχ γιατι δεν γινεται να την υψωσουμε στο τετραγωνο και να αντικαταστησουμε το ημ(τετραγωνο)χ
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
filomathis
Εκκολαπτόμενο μέλος


Και αν το δουλεψεις και στην φυσικη και σου λεει για 1η φορα μετα την t=0 στην η χ=2κπ +π θα πεις για κ=0 χ=π 1η φορα
ενω εδω χ=2κπ -π θα πεις 1η φορα για κ=1 γιατι για κ=0 εχεις αρνητικη γωνια ισως και για αυτο.Δεν ξερω αν σε βοηθησα :p
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
eyb0ss
Δραστήριο μέλος


ΔιότιΣτην εξισωση συνχ=-1 γιατι λυση ειναι μονο η χ=2κπ +π και οχι η χ=2κπ -π ;
Όμως
οπότε το
Απλά σκέψου ότι τα πολλαπλάσια της μορφής
Γίνεται... ΑΛΛΆ πρέπει το ημίτονο των λύσεων που βρήκες να είναι αρνητικό, (μηδέν δεν γίνεται γιατί δεν βγάζει αληθή ισότητα)την εξισωση 3συνχ=-ριζα3ημχ γιατι δεν γινεται να την υψωσουμε στο τετραγωνο και να αντικαταστησουμε το ημ(τετραγωνο)χ
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Γατόπαρδος.
Πολύ δραστήριο μέλος


εφ(2χ+π/3)=σφ(χ+π/3)
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Στην πραγματικότητα πρόκειται για τα ίδια σύνολα λύσεων οπότε μπορείς να γράψεις ή το ένα ή το άλλο. Και αυτό φαίνεται απ' το γεγονός ότι κάθε λύση απ' το πρώτο σύνολο λύσεων μπορεί να γραφεί σαν λύση από το δεύτερο σύνολο λύσεων και αντίστροφα. Δηλαδή1)Στην εξισωση συνχ=-1 γιατι λυση ειναι μονο η χ=2κπ +π και οχι η χ=2κπ -π ;
Μπορείς να το κάνεις, απλά πριν υψώσεις στο τετράγωνο θα πρέπει να πάρεις περιορισμό για το x ώστε τα δύο μέλη να είναι ομόσημα. Δηλαδή2)την εξισωση 3συνχ=-ριζα3ημχ γιατι δεν γινεται να την υψωσουμε στο τετραγωνο και να αντικαταστησουμε το ημ(τετραγωνο)χ
Λύνοντας την πρώτη εξίσωση παίρνουμε τις λύσεις
από τις οποίες κρατάμε μόνο το δεύτερο σύνολο
γιατί μόνο αυτά τα x πέφτουν στο 4ο τεταρτημόριο και συνεπώς συμφωνούν με τον περιορισμό που θέσαμε. Λύνοντας την δεύτερη εξίσωση παίρνουμε τις λύσεις
από τις οποίες κρατάμε μόνο το πρώτο σύνολο
γιατί μόνο αυτά τα x πέφτουν στο 2ο τεταρτημόριο και συνεπώς συμφωνούν με τον περιορισμό που θέσαμε.
Υ.Γ.: Να σημειώσω ότι θεώρησα πως η εξίσωση είναι
Θυμήσου ότι γενικάΩραια θελω μια βοηθεια σε αυτην
εφ(2χ+π/3)=σφ(χ+π/3)
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Γατόπαρδος.
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
eyb0ss
Δραστήριο μέλος


ποιά είναι η περίοδος της συνάρτησης f(x)=ημ(χ-π/6)?
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Γατόπαρδος.
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
eyb0ss
Δραστήριο μέλος


Έστω ότι γράφεται ως άθροισμα τετραγώνων. Τότεπώς κάνω άθροισμα τετραγώνων αυτό 4x²-xy-18y² ?
Για
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Γατόπαρδος.
Πολύ δραστήριο μέλος


6^x + 6^x+1 =2^x + 2^x+1 + 2^x+2
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
eyb0ss
Δραστήριο μέλος


Δεν μπορείς να σπάσεις τα εκθετικά έτσι. Για x=0 δεν ισχύει. Μήπως εννοείςάρα έχω κάνει λάθος εγώ μήπως μπορείς να βοηθήσεις?
6^x + 6^x+1 =2^x + 2^x+1 + 2^x+2
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Γατόπαρδος.
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
eyb0ss
Δραστήριο μέλος


Ναι αυτό εννοώ
Και στα δυο μέλη έχουμε αθροίσματα όρων γεωμετρικής προόδου. Στο αριστερό μέλος έχουμε 2 όρους και λόγο 6 ενώ στο δεξί 3 όρους και λόγο 2. Οπότε
Πώς δεν το σκέφτηκα νωρίτερα με ξεπερνάει.
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Γατόπαρδος.
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
eyb0ss
Δραστήριο μέλος


Έστωκαμια βοήθεια σε αυτή?την προσπάθησα αρκετά
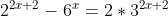
Αυτή την τετραγωνική μορφή μορφή την παραγοντοποίησα προηγουμένως ως
άρα
Πιστεύω πως υπάρχει πιο εύκολος εναλλακτικός δρόμος, αν τον βρω τον ποστάρω εδώ.
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Άλλη μία λύσηκαμια βοήθεια σε αυτή?την προσπάθησα αρκετά
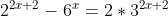
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 1 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 46 μέλη διάβασαν αυτό το θέμα:
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki



