Ναυσικά
Δραστήριο μέλος


υποδειξουλα γιοκ?Θέμα προετοιμασίας για όσους δώσουν μαθηματική εταιρία...
Άσκηση by me:
Ανκαι ισχύει:
,
Να δειχθεί ότι:
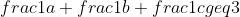

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
mostel
Πολύ δραστήριο μέλος


Στέλιος
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
djimmakos
Διάσημο μέλος


Η υπόδειξη δόθηκε από τον lostg..! Αν θες ανάτρεξε λίγο στα προηγούμενα ποστς για να τη δεις !
Στέλιος
Μάλλον έχουν ανανεώσει τη σελίδα και το λινκ αυτό σε βγάζει σε μια σελίδα με τις βασικές ταυτότητες στο R
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Ναυσικά
Δραστήριο μέλος


Μάλλον έχουν ανανεώσει τη σελίδα και το λινκ αυτό σε βγάζει σε μια σελίδα με τις βασικές ταυτότητες στο R
και εκτος αυτου αν πατησεις το λινκ με τις ανισωσεις cauchy στο τέλος σου βγάζει error 404 http page not found για κάποιο λόγο.....
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
djimmakos
Διάσημο μέλος


Τώρα από τι σχέση a+b+c=3 πρέπει να λύσουμε ως προς έναν άγνωστο και να το κάνουμε αντικατάσταση μέσα στην ανίσωση και λογικά πρέπει να καταλήξουμε σε μια ανισοταυτότητα που να ισχύει...
Αλλά δεν

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lostG
Εκκολαπτόμενο μέλος


Όχι Ναυσικά.Οι σύνδεσμοι είναι ενεργοί.Χρησιμοποίησε Internet Explorer καί όχι κάποιον άλλον browser.και εκτος αυτου αν πατησεις το λινκ με τις ανισωσεις cauchy στο τέλος σου βγάζει error 404 http page not found για κάποιο λόγο.....
Να κάνουμε κάτι άλλο τότε.Να τις αποθηκεύσουμε καί να τις ανεβάσουμε σαν αρχεία έτοιμα γιά κατέβασμα.
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Ναυσικά
Δραστήριο μέλος


Όχι Ναυσικά.Οι σύνδεσμοι είναι ενεργοί.Χρησιμοποίησε Internet Explorer καί όχι κάποιον άλλον browser.
Να κάνουμε κάτι άλλο τότε.Να τις αποθηκεύσουμε καί να τις ανεβάσουμε σαν αρχεία έτοιμα γιά κατέβασμα.
γτ δλδ με firefox δεν ανοίγει???αααα δν μας τα λεει καλα ο browserakos και θα τον απολύσω μου φαίνεται.....
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lostG
Εκκολαπτόμενο μέλος


γτ δλδ με firefox δεν ανοίγει???αααα δν μας τα λεει καλα ο browserakos και θα τον απολύσω μου φαίνεται.....
Όχι μιά χαρά είναι η αλεπού αλλά τα αρχεία απ΄ότι θυμάμαι όταν γράφτηκαν δούλευαν με τον ΙΕ ενώ με την αλεπού της τότε εποχής(Φεβρουάριος 2007) δεν λειτουργούσαν.Όμως τώρα πού τα ανοίγω εδώ δουλεύουν με όλους τούς browsers ακόμη καί με τον τελευταίο Opera πού τον έχω σε portable έκδοση στο memory stick.Τελικά δεν σού ανοίγουν οι σελίδες?
Πολλές φορές παίζει ρόλο καί ποιά έκδοση Java χρησιμοποιεί ο browser ώστε νε εμφανίζει σωστά τις σελίδες.
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
djimmakos
Διάσημο μέλος



Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Ναυσικά
Δραστήριο μέλος



(πλάκα πλάκα παίζει να πρέπει να υψώσω και στο τετράγωνο για να κάνω τη ρίζα.....
 )
)Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
djimmakos
Διάσημο μέλος


εγω το ξεκίνησα έτσι ώστε στον παρονομαστη να χω α+β+γ αλλα τίποτα.....μετα προσπάθησα απαλοιφή......τωρα ψαχνω τη σύνδεση με την ανισότητα cauchy που θα μ παει η ρημαδοασκηση μια 2 τρεις θα τη λύσω τη χαζή!όχι που θα μου βγει κι από πάνω....
(πλάκα πλάκα παίζει να πρέπει να υψώσω και στο τετράγωνο για να κάνω τη ρίζα.....)
Εδώ εμείς λέμε να ξεφύγουμε από τη ρίζα, εσύ τι τι θες; :p
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
mostel
Πολύ δραστήριο μέλος


Θέλουμε να δείξουμε ότι:
'Ομως ισχύει:
Αυτό γιατί:
΄΅Ετσι:
Άρα:
Άρα:
Επομένως αρχικά ζητούσαμε να δειχθεί ότι (1):
Τώρα, αρκεί να δείξουμε ότι:
ή
Αφού ισχύει όμως:
θα ισχύει και:
Δηλαδή, αν θέσουμε
Όμως από την ταυτότητα του Euler (βιβλίο πρώτης λυκείου), έχουμε ότι:
Επειδή
Και αν ξανακάνουμε την αντικατάσταση:
Άρα η ανίσωση έχει αποδειχθεί.
Στέλιος
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
djimmakos
Διάσημο μέλος


Τώρα για να την έλυνα...μπα
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Hurr
Εκκολαπτόμενο μέλος


Τις ταυτότητες τις ξέρω....
Τώρα για να την έλυνα...μπα
Φυσιολογικο ειναι μην ανησυχεις. Εξασκηση θελει
Και με μερικες γνωστες ανισοτητες θα σου βγαινουν ευκολα τετοιες ασκησεις
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
djimmakos
Διάσημο μέλος


Φυσιολογικο ειναι μην ανησυχεις. Εξασκηση θελει
Και με μερικες γνωστες ανισοτητες θα σου βγαινουν ευκολα τετοιες ασκησεις
Εγώ ο καημένος προσπαθούσα να φτάσω σε κάποια ανισοταυτότητα τύπου

Tελικά με την ανισοτητα του cachy ηταν πιο ευκολη
Ευχαριστώ lostG :thanks:
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Hurr
Εκκολαπτόμενο μέλος


Για περιπλοκες ασκησεις δεν ειναι παντα τοσο ευκολο αυτοΕγώ ο καημένος προσπαθούσα να φτάσω σε κάποια ανισοταυτότητα τύπου

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
kvgreco
Εκκολαπτόμενο μέλος


Αρχική Δημοσίευση από mostel:Άρα:
.
Επομένως αρχικά ζητούσαμε να δειχθεί ότι (1):

Τώρα, αρκεί να δείξουμε ότι:


ή
mostel πώς προκύπτουν ισοδύμναμα δηλαδή ότι αν x+y+z<=10 και εγώ θέλω να δείξω ότι x+y+z>=k λες να πάρω 10>=k .Δεν νομίζω πως στέκει κάτι τέτοιο.Γιά δες το καλύτερα.Πως γίνεται?
Βάλε κ=6 όμως μπορεί το άθροισμα να ισούται με 5 γιά παράδειγμα οπότε δεν ισχύουν.
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
djimmakos
Διάσημο μέλος


Θέτουμε:
n = 3
α1=α
α2=b
α3= c
Παίρνωντας από την ανισότητα του Cachy το παρακάτω κομμάτι:
έχουμε:
και κάνοντας χιαστί παίρνουμε το ζητούμενο
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
mostel
Πολύ δραστήριο μέλος


mostel πώς προκύπτουν ισοδύμναμα δηλαδή ότι αν x+y+z<=10 και εγώ θέλω να δείξω ότι x+y+z>=k λες να πάρω 10>=k .Δεν νομίζω πως στέκει κάτι τέτοιο.Γιά δες το καλύτερα.Πως γίνεται?
Βάλε κ=6 όμως μπορεί το άθροισμα να ισούται με 5 γιά παράδειγμα οπότε δεν ισχύουν.
Εχεις δικαιο σε υατο που λες, μου εφυγε. Αν αφήσεις το τελευταίο κομμάτι όμως και πάρεις το τελευταίο πόρισμα (δηλαδή απ' το abc\leq 1 και τη συνεχίσεις, βγαίνει κανονικά)
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Iliaso
Περιβόητο μέλος



Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 10 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 51 μέλη διάβασαν αυτό το θέμα:
- akis_95
- cment
- Fanimaid123
- Satan Claus
- eva987
- _Aggelos123
- Cat lady
- Γιούρα
- spring day
- ggl
- tsiobieman
- Σωτηρία
- το κοριτσι του μαη
- eukleidhs1821
- Georgekk
- SlimShady
- Scandal
- Lia 2006
- Alexandros36k
- 69lover
- TonyMontanaEse
- Unboxholics
- Arvacon
- rafaela11
- Hara_2
- manos66
- Ryuzaki
- Giii
- Athens2002
- barkos
- ssalex
- anastasiakan
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

