Hurr
Εκκολαπτόμενο μέλος


Είναι συμπαθητική άσκηση, απλώς αν την έβαζες π.χ. στο σχολείο θα έτρωγες άπειρο κράξιμο
Καλά έκανες πάντως και την έβαλες, για να με (μας) κρατάς σε μια επαφή με την πανέμορφη ευκλείδια γεωμετρία, την οποία δυστυχώς έχω παρατήσει από τότε που έδωσα τελευταία φορά εξετάσεις σε μαθηματικούς διαγωνισμούς.
Στέλιος
Στο σχολειο φιλε μου τουλαχιστον στο δικο μου αρκετοι δεν μπορουσαν ουτε διαφορα τετραγωνων να κανουν..
Ασε εχει περασει καιρος.. και γω αρχιζω και τα ξεχνω
Στο πανεπιστημιο εχει διαγωνισμους?
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Hurr
Εκκολαπτόμενο μέλος


Απλά η λυση στο forum για να φανει να πρεπει να πατησει οποιος θελει να τη δει σε ενα συνδεσμο. Πρεπει να υπαρχει η δυνατοτητα αυτη αλλα δεν την εχω βρει ακομαΤι ακριβώς εννοείς?
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
peri
Νεοφερμένος


Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Hurr
Εκκολαπτόμενο μέλος


1)Να λυθεί το συστημα των εξισώσεων
2)Αν
Nα δειχθεί οτι
Είναι λίγο ως αρκετα απαιτητικές.
Αν ψαξετε το θεμα για παρομοιες ασκησεις η 1η βγαίνει σχετικα εύκολα
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
zidane4ever
Νεοφερμένος


Ζ1,Ζ2,Ζ3ΕC,lZ1l=1,lZ2l=2,lZ3l=4 να αποδειξετε οτι Ζ1+Ζ2+Ζ3 δεν μπορει να ειναι ισο με το μηδεν....παρακαλω απαντηστε μου ...
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lostG
Εκκολαπτόμενο μέλος


Έστω κάνει μηδέν τότε z3=-z1-z2 θα είναι |z3|=|-z1-z2|=|z1+z2|Θελω αμεσα βοηθεια!Θελω να αποδειξω οτι εαν
Ζ1,Ζ2,Ζ3ΕC,lZ1l=1,lZ2l=2,lZ3l=4 να αποδειξετε οτι Ζ1+Ζ2+Ζ3 δεν μπορει να ειναι ισο με το μηδεν....παρακαλω απαντηστε μου ...
Αλλά |z1+z2|<=|z1|+|z2|=3
όμως |z3|=4
Άτοπο επομένως.
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
zidane4ever
Νεοφερμένος


Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Hurr
Εκκολαπτόμενο μέλος


Θελω αμεσα βοηθεια!Θελω να αποδειξω οτι εαν
Ζ1,Ζ2,Ζ3ΕC,lZ1l=1,lZ2l=2,lZ3l=4 να αποδειξετε οτι Ζ1+Ζ2+Ζ3 δεν μπορει να ειναι ισο με το μηδεν....παρακαλω απαντηστε μου ...
τελεια απαντηση αλλα μηπως υπαρχει και αλλος τροπος?...
Γνωρίζουμε ότι ισχύει ο τύπος
Σημείωση: Η ταυτοτητα αυτη θέλει αποδειξη για να την χρησιμοποιησετε.
Αν θυμαμαι καλα ειναι ασκηση στο βιβλιο
Για
Η παραπανω ταυτοτητα γινεται
Εστω ότι
τοτε
Με αντικατασταση στην (1)
Ουσιαστικα αποφυγαμε την τριγωνικη. Η απαντηση όμως του LostG ειναι σαφως καλύτερη
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
zidane4ever
Νεοφερμένος


Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lostG
Εκκολαπτόμενο μέλος


Γιατί φίλοι μου δεν είναι το παν το χρήμα.Εγώ τουλάχιστον δεν έχω αυτή τη στάση ζωής.Όπως όταν λέω σε συναδέλφους ότι μπείτε ρε σείς σε διάφορα φόρα(sic) να μοιράζετε τις γνώσεις σας απαντούν κυνικά.Κι εγώ τι θα κερδίσω!
Τούς λέω ότι σκεφτείτε ένα παιδί γιά παράδειγμα στο Καστελόρριζο (όπου οι επιλογές είναι ελάχιστες έως ανύπαρκτες) καί αυτό το παιδί δεν έχει τις ευκαιρίες των "μοσχανεθρεμένων" δικών σας παιδιών.
Το διαδίκτυο είναι ευλογία καί κατάρα μαζί.Το ζήτημα είναι πως το χρησιμοποιεί κάποιος.Πράγμα πού έχει να κάνει βέβαια με την συνολική συγκρότηση κάθε χρήστη.
Χρησιμοποίησε το |z|^2=z(z*), z* είναι ο συζυγής τού z.ποια ειναι η αποδειξη της για να μπορω να την χρησιμοποιω?
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Hurr
Εκκολαπτόμενο μέλος


Άλλες 2 ασκήσεις :
1)Να λυθεί το συστημα των εξισώσεων
2)Αν
Nα δειχθεί οτι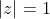
Είναι λίγο ως αρκετα απαιτητικές.
Αν ψαξετε το θεμα για παρομοιες ασκησεις η 1η βγαίνει σχετικα εύκολα
Μιας και εμειναν καιρο χωρις καμια απαντηση η προσπαθεια
να πω λυσεις η καποια υποδειξη ?
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
m3Lt3D
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Hurr
Εκκολαπτόμενο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
m3Lt3D
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Hurr
Εκκολαπτόμενο μέλος


βασικα ολη η ουσια μια παραγοντοποιηση δεν ειναι?
Η παραγοντοποιηση παιζει κρισιμο ρολο στη λυση. Τουλαχιστον τη λυση που εχω βρει εγω. Μπορει βεβαια να υπαρχει και ευκολοτερος τροπος και να μη τον εχω δει!!
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
m3Lt3D
Πολύ δραστήριο μέλος


πωωω εχω δοκιμασει ολους τους συνδιασμους, εχω δοκιμασει και να βγαλω σε αυτους τους συνδιασμους διαφορα i απεξω, αλλα τπτ!Η παραγοντοποιηση παιζει κρισιμο ρολο στη λυση. Τουλαχιστον τη λυση που εχω βρει εγω. Μπορει βεβαια να υπαρχει και ευκολοτερος τροπος και να μη τον εχω δει!!
στο τσακ ειμαι να βαλω αναλυτικη μορφη και να λυνω βραδυατικα (x+yi)^10!!!



Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Hurr
Εκκολαπτόμενο μέλος


πωωω εχω δοκιμασει ολους τους συνδιασμους, εχω δοκιμασει και να βγαλω σε αυτους τους συνδιασμους διαφορα i απεξω, αλλα τπτ!
στο τσακ ειμαι να βαλω αναλυτικη μορφη και να λυνω βραδυατικα (x+yi)^10!!!
Ωραια ιδεα το αναπτυγμα θα το δοκιμασω





Οταν την ελυνα μου εσπασε τα νευρα μεχρι να το βρω. Ακομα δεν ειμαι 100 % σιγουρος γιατι αυτα που βγαζω μου φαινονται περιεργα
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
manos66
Εκκολαπτόμενο μέλος


...
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
maltanous
Νεοφερμένος



Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
m3Lt3D
Πολύ δραστήριο μέλος


Καλησπέρα παιδιά,είμαι λιγο καινούργιος γι'αυτό θέλω να ρωτήσω αν γίνεται να ποστάρω κ γω μια άσκηση η οποία με έχει παιδέψει αρκετά...
οχι βεβαια!!! τι νομιζες πως ειναι εδω περα; σχολειο; πρωτα συμπληρωνεις μια αιτηση που θα βρεις στα πανω αριστερα στην οθονη σου. Επειτα...



Φυσικα και μπορεις ρε συ! Αυτος εξαλου ειναι ενας απο τους σκοπους του φορουμ Γ' Λυκείου & Απόφοιτοι > Θετική & Τεχνολογική
Αν ειναι και καμια ωραια, χαρη θα μας κανεις που την ποσταρεις, δεν θα σου εχουμε κανει εμεις χαρη που την λυσαμε!

Αλλα και απλη να'ναι δεν πειραζει!(ο καλος ο μυλος...
 )
)Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 5 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 1 μέλη διάβασαν αυτό το θέμα:
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

