Έστω η καμπύλη C που ορίζεται από τις παραμετρικές εξισώσεις x=f(t) και y=g(t). Αν οι συναρτήσεις f, g έχουν ολοκληρώσιμες παραγώγους στο διάστημα [α,β] τότε:
Το μήκος του τόξου S της καμπύλης C που ορίζεται από τα σημεία
,y(alpha ) right))
και
,y(beta ) right))
υπολογίζεται από την σχέση:
=int_{alpha }^{beta }leftsqrt{{left[f'(t)] right}^{2}+{left[g'(t)] right}^{2}}dt)
έχεις δει ποτέ σου την απόδειξη της σχέσης του μήκους τόξου καμπύλης στον IR3 που να ορίζεται από τις παραμετρικές εξισώσεις;

Θα ήθελα σε αυτό το topic να γράψουμε πολλά θεωρήματα και αποδείξεις από πολλούς κλάδους ανώτερων μαθηματικών (όπως τοπολογία, θεωρία τελεστών, διαφορική γεωμετρία, θεωρία ομάδων, μαθηματική φυσική, αριθμητική ανάλυση,...κτλ). Πολύ καλή δουλειά έχεις κάνει Civilara, όπως πολύ καλή δουλειά κάνετε όλοι υπόλοιποι...Σύντομα, θα παραθέσω και γω ένα κομματάκι από τις γνώσεις μου, με σκοπό την σωστή μελέτη των ανώτερων μαθηματικών...
-----------------------------------------
Κάνω μια λεπτομερή διατύπωση κάποιων εννοιών, όπως πολύ σωστά παρέθεσε ο συνάδελφος statakos.
1.Οι σχέσεις:
Έστω
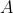
,
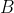
δυο μη κενά σύνολα. Κάθε υποσύνολο
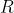
του
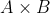
λέγεται
διμελής σχέση ή
σχέση από το
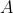
στο
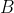
. Μια διμελής σχέση από το
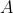
στο
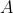
λέγεται
σχέση επί του
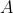
. Αν
 \in R)
τότε γράφουμε
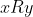
και διαβάζουμε: «το
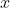
πληρεί την σχέση με το
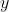
».
2.Οι ποιοτικές ιδιότητες μιας σχέσης:
Μια σχέση
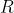
επί του συνόλου
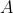
λέγεται:
- αυτοπαθητική ή ανακλαστική, αν
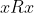 για κάθε
για κάθε 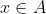
- συμμετρική, αν
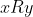
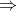
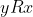 , για κάθε
, για κάθε 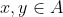
- μεταβατική, αν
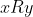 ,
, 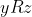
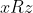 , για κάθε
, για κάθε 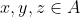
- αντισυμμετρική, αν
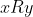 ,
, 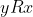
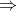
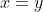 , για κάθε
, για κάθε 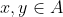
3.H Σχέση Ισοδυναμίας:
Μια σχέση επί ενός συνόλου Α λέγεται
σχέση ισοδυναμίας, αν είναι αυτοπαθητική, συμμετρική και μεταβατική. Χρησιμοποιούμε το σύμβολο "
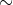
". Συνεπώς:
4. H Kλάση Σχέσης Ισοδυναμίας:
Έστω ένα σύνολο
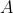
και μια σχέση ισοδυναμίας επί του Α.
Κλάση ενός στοιχείου
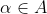
ως προς την σχέση ισοδυναμίας λέγεται το σύνολο
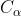
={
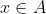
:
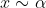
}. Η κλάση ισοδυναμίας στην οποία ανήκει ένα σύνολο
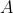
λέγεται
πληθάριθμος ή
πληθικός αριθμός του
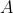
και γράφουμε συμβολικά, Card
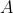
ή
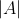
.