Λογικό σφάλμα. Ας κάνουμε έναν διαχωρισμό.
Έστω ότι p, q είναι δύο ισχυρισμοί και θέλουμε να αποδείξουμε την συνεπαγωγή

. Υπάρχουν δύο τρόποι.
- Ξεκινάμε από τον ισχυρισμό p και με διαδοχικές συνεπαγωγές καταλήγουμε στον q . Δηλαδή
 . Για παράδειγμα έστω ότι θέλω να δείξω ότι ισχύει ο ισχυρισμός
. Για παράδειγμα έστω ότι θέλω να δείξω ότι ισχύει ο ισχυρισμός ^2 \geq 4ab ) . Τότε ξεκινώντας από τον ισχυρισμό
. Τότε ξεκινώντας από τον ισχυρισμό ^2 \geq 0) o οποίος είναι αληθής έχουμε διαδοχικά
o οποίος είναι αληθής έχουμε διαδοχικά ^2 \geq 0 \Rightarrow a^2-2ab+b^2 \geq 0 \Rightarrow a^2+2ab+b^2\geq 4ab \Rightarrow (a+b)^2 \geq 4ab )
- Επειδή κάποιες φορές δεν είναι προφανής ο αληθής ισχυρισμός p από τον οποίο πρέπει να ξεκινήσουμε, λειτουργούμε ως εξής: Για να ισχύει ο q αρκεί να ισχύει ο l,... αρκεί να ισχύει ο s, αρκεί να ισχύει ο r, αρκεί να ισχύει ο p ο οποίος είναι αληθής. Στην παραπάνω περίπτωση θα είχαμε δηλαδή:
^2 \geq 4ab \Leftarrow a^2+2ab+b^2\geq 4ab\Leftarrow a^2-2ab+b^2 \geq 0 \Leftarrow (a-b)^2) που είναι ουσιαστικά η ίδια σειρά συνεπαγωγών με πάνω. Να σημειωθεί εδώ ότι με την "μέθοδο του αρκεί" χρησιμοποιούμε καταχρηστικά (έτσι το έχει και το σχολικό σε κάποιες αποδείξεις) το σύμβολο τις διπλής ισοδυναμίας
που είναι ουσιαστικά η ίδια σειρά συνεπαγωγών με πάνω. Να σημειωθεί εδώ ότι με την "μέθοδο του αρκεί" χρησιμοποιούμε καταχρηστικά (έτσι το έχει και το σχολικό σε κάποιες αποδείξεις) το σύμβολο τις διπλής ισοδυναμίας 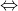 απαιτώντας έτσι να ισχύουν και οι δεξιές συνεπαγωγές
απαιτώντας έτσι να ισχύουν και οι δεξιές συνεπαγωγές 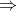 κάτι το οποίο κανονικά είναι περιττό γιατί δεν μας ενδιαφέρει η συνεπαγωγή
κάτι το οποίο κανονικά είναι περιττό γιατί δεν μας ενδιαφέρει η συνεπαγωγή  . Ας δεχθούμε παρ' όλα αυτά το σύμβολο της διπλής ισοδυναμίας μιας και έτσι έχει επικρατήσει.
. Ας δεχθούμε παρ' όλα αυτά το σύμβολο της διπλής ισοδυναμίας μιας και έτσι έχει επικρατήσει.
Έκανα την εισαγωγή αυτή για να δεις ξανά τα βήματα της απόδειξης και να καταλάβεις το λογικό σφάλμα. Εδώ δηλαδή θεωρούμε τους ισχυρισμούς
(y+\sqrt{y^2+1})=1)
και

και θέλουμε να δείξουμε ότι

δηλαδή
"αν ο p είναι αληθής τότε και ο q είναι αληθής". Στην πορεία της απόδειξής σου προσπάθησες να ακολουθήσεις την 2η μέθοδο του αρκεί. Όμως από πουθενά δεν προκύπτει ότι ισχύει η συνεπαγωγή

παρά μόνο η

. Με άλλα λόγια υπέθεσες ότι ισχύει το συμπέρασμα q και ΜΟΝΟ με δεξιές συνεπαγωγές κατέληξες στην αλήθεια της υπόθεσης p. Αν βέβαια ίσχυαν οι αριστερές συνεπαγωγές η λύση σου θα ήταν σωστή όπως και τόσες άλλες λύσεις σου που έχουν γίνει με τον ίδιο τρόπο. Ελπίζω να κατάλαβες την διαφορά.
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.



που επαληθευει τις σχεσεις .
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki





