eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.965 μηνύματα.

24-03-21

16:02
νομιζω το κουραζεις πολυΒάζεις όπου α το x και όπου β κάποιο τυχαίο πραγματικό x0.
Θα ισχύει |g(x)-g(x0)|<=|x-x0| <=> -|x-x0|<= g(x)-g(x0)<=|x-x0|. Με κ.π. δείχνεις ότι η g είναι συνεχής οπότε και η f θα είναι συνεχής. Έστω ότι η f δεν είναι 1-1 δηλαδή ότι υπάρχουν πραγματικά x1,x2 τ.ω. f(x1)=f(x2) με x1,x2 διάφορα. Τότε g(x1)-2*x1=g(x2)-2*x2 <=> [g(x2)-g(x1)]/(x2-x1) = 2 που είναι άτοπο διότι
-1 <= [g(x2)-g(x1)]/(x2-x1) <= 1. Άρα η f είναι 1-1 και συνεχής και με το λινκ παραπάνω δείχνουμε πως είναι και γνησίως μονότονη. Επίσης f(1)-f(0)=g(1)-g(0)-2<0 επειδή |g(1)-g(0)|<= 1 επομένως g(1)- g(0) <= 1 < 2 και τελικά f(1)<f(0) άρα είναι γνησίως φθίνουσα
Edit: Τελικά υπήρχε πιο κομψός τρόπος, κάπως έτσι τα έλυνα εκείνη τη χρονιά και με καντήλιαζε ο καθήγητης.
bovid19
Εκκολαπτόμενο μέλος
Ο bovid19 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 27 ετών και Πτυχιούχος του τμήματος Οικονομικής Επιστήμης ΟΠΑ. Έχει γράψει 344 μηνύματα.

24-03-21

16:04
Πάλι σωστό είναι fight meνομιζω το κουραζεις πολυ
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.965 μηνύματα.

24-03-21

16:07
απλα για να ναι ορθα ολα επρεπε να γραφει η εκφωνηση για καθε α,β στους πραγματικους διοτι ετσι ειναι λιγο φλου.
Μάρκος Βασίλης
Πολύ δραστήριο μέλος
Ο Βασίλης αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 29 ετών, Διδακτορικός και μας γράφει από Καισαριανή (Αττική). Έχει γράψει 1.871 μηνύματα.

24-03-21

20:34
Δεν είναι αποδεκτό πλέον το 1-1 + συνεχής => γνησίως μονότονη χωρίς απόδειξη
Ας δώσω άλλη μια:View attachment 78048
Αυτό που αξίζει σε αυτήν την άσκηση είναι η διαίσθηση. Η g, από τις υποθέσεις, δε διαστέλλει τα διαστήματα πραγματικών αριθμών - πιο μπακάλικα, δεν «απομακρύνει» αριθμούς. Από την άλλη, η h(x)=-2x είναι (γνησίως φθίνουσα και) διαστολή, υπό την έννοια ότι πάντοτε:
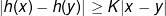
(γενικά Κ>1 και στην περίπτωσή μας, Κ=2 και ισχύει πάντα ισότητα). Ως εκ τούτου, η h «ανοίγει» την απόσταση περισσότερο από ό,τι μπορεί να τη «μαζέψει» η g και άρα οι h,f έχουν την ίδια μονοτονία. Γενικά, αν g όπως παραπάνω και h γνησίως μονότονη διαστολή τότε η f,h έχουν το ίδιο είδος μονοτονίας. Αυτό είναι άμεσο, αφού αν x<y και h γνησίως φθίνουσα τότε:
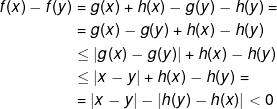
άρα f(x)<f(y) και άρα η f είναι γνησίως αύξουσα. Ανάλογα, αν h γνησίως φθίνουσα τότε:
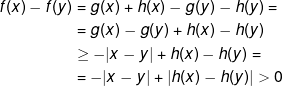
οπότε f(x)>f(y) και άρα η f είναι γνησίως φθίνουσα. Επομένως, η παραπάνω άσκηση μπορεί να γίνει πιο «τρομακτική» αν δώσει κανείς κάποια πιο «κακιά» h(x) αντί της -2x.
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.965 μηνύματα.

24-03-21

21:29
α ρε μαρκο εισαι φοβερος.αυτοι που σκανε πολλα ευρωπουλα σε φροντιστηρια σιγα μην τα μαθαινουν οπως τα λες εσυ.τυχεροι οι μαθητες σου
Μάρκος Βασίλης
Πολύ δραστήριο μέλος
Ο Βασίλης αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 29 ετών, Διδακτορικός και μας γράφει από Καισαριανή (Αττική). Έχει γράψει 1.871 μηνύματα.

26-03-21

14:55
α ρε μαρκο εισαι φοβερος.αυτοι που σκανε πολλα ευρωπουλα σε φροντιστηρια σιγα μην τα μαθαινουν οπως τα λες εσυ.τυχεροι οι μαθητες σου
Ευχαριστώ, αν και το τυχεροί είναι πολλές φορές υποκειμενικό, γιατί πολλές φορές μπορεί να ξεφύγει κανείς και να μπερδέψει τα παιδιά αντί να τα βοηθήσει. :Ρ Αλλά αυτό το δείχνει η πορεία.

eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.965 μηνύματα.

26-03-21

15:31
ναι μπορει να συμβει αυτο απλα απο το να πεις στειρα μεθοδολογια δεν εντυπωνεται στον αλλον οποτε υπο αυτη την εννοια το ειπαΕυχαριστώ, αν και το τυχεροί είναι πολλές φορές υποκειμενικό, γιατί πολλές φορές μπορεί να ξεφύγει κανείς και να μπερδέψει τα παιδιά αντί να τα βοηθήσει. :Ρ Αλλά αυτό το δείχνει η πορεία.
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 12.130 μηνύματα.

26-03-21

18:18
Ωραία ασκησούλα πράγματιΔεν είναι αποδεκτό πλέον το 1-1 + συνεχής => γνησίως μονότονη χωρίς απόδειξη
Ας δώσω άλλη μια:View attachment 78048
 .
.eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.965 μηνύματα.

26-03-21

18:38
το λυσα βρε.ακριβως τα ιδια κανουμε με αλλες μεταβλητες
Alexandros28
Δραστήριο μέλος
Ο Alexandros28 αυτή τη στιγμή δεν είναι συνδεδεμένος. Έχει γράψει 750 μηνύματα.

26-03-21

22:35
Άλλη μια που φαίνεται αρκετά απλή αλλά δεν είναι και τόσο.

[automerge]1616791920[/automerge]
[automerge]1616792142[/automerge]

[automerge]1616791920[/automerge]
[automerge]1616792142[/automerge]
SlimShady
Πολύ δραστήριο μέλος
Ο Κωνσταντίνος αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 21 ετών, Φοιτητής του τμήματος Νομικής ΕΚΠΑ και μας γράφει από Μελίσσια (Αττική). Έχει γράψει 963 μηνύματα.

31-03-21

11:55
Είναι σωστή η λύση μου;
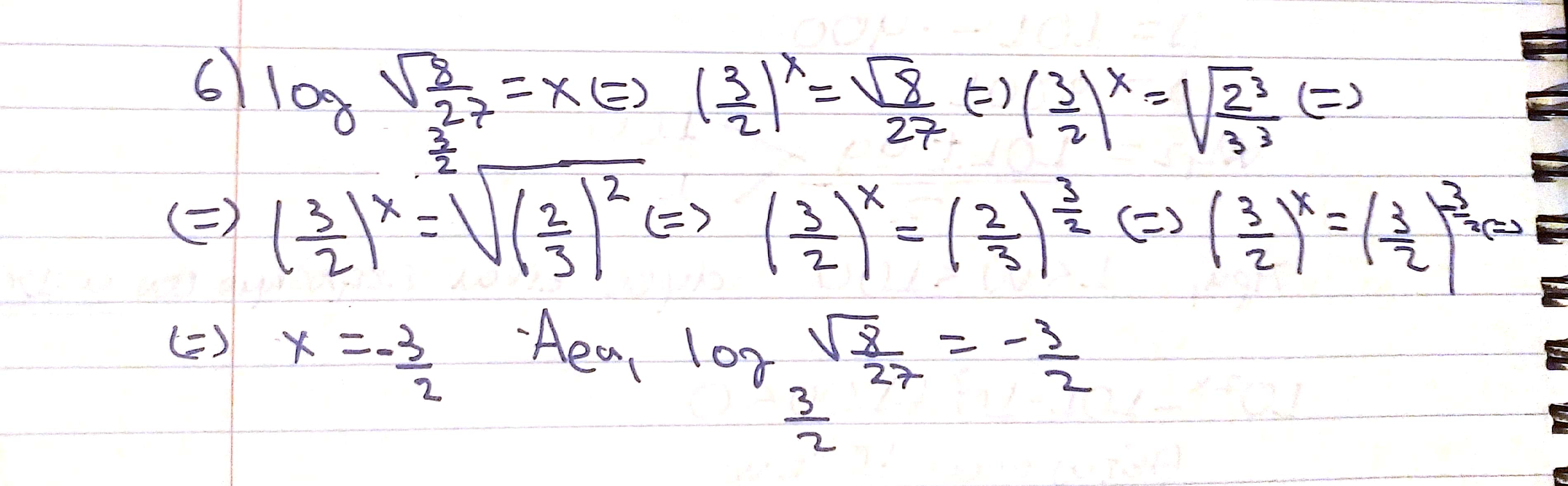
ιωαννηs
Επιφανές μέλος
Ο ιωαννηs αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 25 ετών, Φοιτητής του τμήματος Πρόγραμμα Ιερατικών Σπουδών και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 15.428 μηνύματα.

31-03-21

12:06
Η ροη σωστη ειναι , θελει λιγο μαστορεμα στην ριζα , στην γραφω.Είναι σωστή η λύση μου;View attachment 78477
[automerge]1617182869[/automerge]
Ερώτηση
SlimShady
Πολύ δραστήριο μέλος
Ο Κωνσταντίνος αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 21 ετών, Φοιτητής του τμήματος Νομικής ΕΚΠΑ και μας γράφει από Μελίσσια (Αττική). Έχει γράψει 963 μηνύματα.

31-03-21

12:41
έχεις δίκιο, γι'αυτό ένιωθα ότι κάτι δεν κόλλαγεΗ ροη σωστη ειναι , θελει λιγο μαστορεμα στην ριζα , στην γραφω.
[automerge]1617182869[/automerge]
Ερώτηση
View attachment 78478
ιωαννηs
Επιφανές μέλος
Ο ιωαννηs αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 25 ετών, Φοιτητής του τμήματος Πρόγραμμα Ιερατικών Σπουδών και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 15.428 μηνύματα.

31-03-21

12:46
ωραια πολυ σωστα λοιπον το εγραψες ,λιγο πιο μακρια η ουριτσα της ριζας να πιανει και τον παρονομαστη.
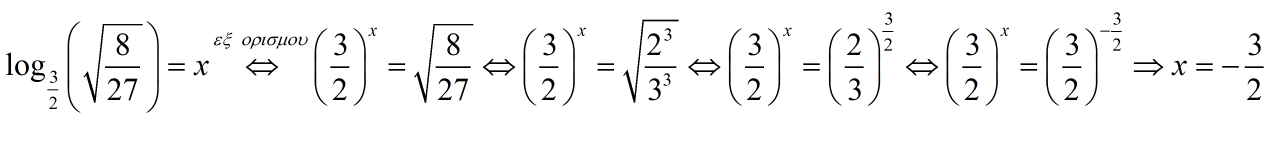
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.965 μηνύματα.

31-03-21

13:11
σωστο ειναι απλα οκ αυτο με τη ριζα που σου πε ο γιαννης και επισης μεσα στη ριζα ειναι στην τριτη οχι στην δευτερα
SlimShady
Πολύ δραστήριο μέλος
Ο Κωνσταντίνος αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 21 ετών, Φοιτητής του τμήματος Νομικής ΕΚΠΑ και μας γράφει από Μελίσσια (Αττική). Έχει γράψει 963 μηνύματα.

04-04-21

15:25
Ζόρικες ασκήσεις, νομίζω ότι τις κατάφερα.
ιωαννηs
Επιφανές μέλος
Ο ιωαννηs αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 25 ετών, Φοιτητής του τμήματος Πρόγραμμα Ιερατικών Σπουδών και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 15.428 μηνύματα.

04-04-21

16:22
Πολυ σωστα τα πηγες ειδικα την πρωτη που εχει την πονηριτσα της.
Τιπ: οταν οι λογαριθμοι εχουν την ιδια βαση μπορεις να το αναφερεις στην αρχη και μετα να το παραλήψεις ενδιαμεσα για να καθαρίσει το ματι σου . Το αναφερεις μονο στο τελος .Και πρόληψη λαθους και ταχυτητα
Τιπ: οταν οι λογαριθμοι εχουν την ιδια βαση μπορεις να το αναφερεις στην αρχη και μετα να το παραλήψεις ενδιαμεσα για να καθαρίσει το ματι σου . Το αναφερεις μονο στο τελος .Και πρόληψη λαθους και ταχυτητα
marian
Νεοφερμένο μέλος
Η marian αυτή τη στιγμή δεν είναι συνδεδεμένη. Είναι 35 ετών και Φοιτήτρια του τμήματος Επιστήμης Υπολογιστών Κρήτης. Έχει γράψει 115 μηνύματα.

04-04-21

21:04
Παιδια ασύμπτωτες έχουν πέσει ποτέ στις πανελλήνιες;
Alexandros28
Δραστήριο μέλος
Ο Alexandros28 αυτή τη στιγμή δεν είναι συνδεδεμένος. Έχει γράψει 750 μηνύματα.

04-04-21

21:08
θεματα πανελλαδικών 2019 & 2018. Δεν έπεσαν πέρυσι επειδή ήταν εκτός ύλης.
SlimShady
Πολύ δραστήριο μέλος
Ο Κωνσταντίνος αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 21 ετών, Φοιτητής του τμήματος Νομικής ΕΚΠΑ και μας γράφει από Μελίσσια (Αττική). Έχει γράψει 963 μηνύματα.

04-04-21

22:13
Η αλήθεια είναι ότι με δυσκόλεψαν σε μεγάλο βαθμό, με αποτέλεσμα να αναθέωρησω πολλαπλές φορές ως προς την επίλυση τους, αλλά από οτι φαίνεται όλα έβησαν καλώς!Πολυ σωστα τα πηγες ειδικα την πρωτη που εχει την πονηριτσα της.
Τιπ: οταν οι λογαριθμοι εχουν την ιδια βαση μπορεις να το αναφερεις στην αρχη και μετα να το παραλήψεις ενδιαμεσα για να καθαρίσει το ματι σου . Το αναφερεις μονο στο τελος .Και πρόληψη λαθους και ταχυτητα
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 2 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 289 μέλη διάβασαν αυτό το θέμα:
- Maynard
- foxypup
- Pars3c
- mikke
- thepigod762
- 98.8%chimpanzee
- trifasikodiavasma
- ggl
- ioanna2007
- Hased Babis
- Mariosm.
- infection54
- Jesse_
- topg
- eukleidhs1821
- bill09876
- Debugging_Demon
- mali
- Joji
- Ness
- Helen06
- Scandal
- synthnightingale
- arko
- BillyTheKid
- Magigi
- Paragontas7000
- Unboxholics
- just some guy
- george777
- Wonderkid
- Micro
- IceCream05
- Abiogenesis
- GeorgePap2003
- katia.m
- giannhs2001
- paul
- Praxis
- Apocalypse
- shezza94
- desp1naa
- rempelos42
- Sherlockina
- oups
- Dimgeb
- spring day
- KingOfPop
- mpapa
- Chrisa
- Physicsstudent
- tsiobieman
- P.Dam.
- persi
- theodoraooo
- PanosBat
- kost28
- mikriarchitectonissa
- BILL KEXA
- Dr. Gl. Luminous
- Eleftheria2
- Lathy
- bruh_234
- Miranda32
- SlimShady
- kallikd
- nucomer
- alpha.kappa
- Eeeee
- J.Cameron
- Marple
- Kitana
- F1L1PAS
- sophiaa
- VFD59
- papa2g
- το κοριτσι του μαη
- srg96
- Hopeful22
- Φινεύς
- Phys39
- Anta2004
- fairyelly
- Pharmacist01
- jYanniss
- Panagiotis849
- Kokro
- augustine
- Nikoletaant
- Mashiro@Iberan
- margik
- Mammy Nun
- Pastramis
- Σωτηρία
- Appolon
- panosveki
- Nickt23
- igeorgeoikonomo
- Steliosgkougkou
- QWERTY23
- Ameliak
- aladdin
- nimbus
- Φωτεινη Τζα.
- marian
- Georgekk
- xrisamikol
- Poirot
- the purge
- Dora140303
- Machris
- s93060
- Nikitas18
- Stif6
- stav.mdp
- damn
- aekaras 21
- Anthropaki
- Angelos12345
- ioannam
- Μάρκος Βασίλης
- skyway
- Nick2325
- Nala
- Manolo165
- Ryuzaki
- T C
- Devilshjoker
- El_
- George9989
- TonyMontanaEse
- globglogabgalab
- constansn
- barkos
- katerinavld
- fenia
- An_uknown_world
- Jimmis18
- maria2001
- KingPoul
- Xara
- thecrazycretan
- abcdefg12345
- Κλημεντίνη
- ale
- panagiotis G
- mechaniceng
- Giii
- calliope
- Tequila
- natalix
- Ουριήλ
- Cortes
- Alexecon1991
- pepsoula
- Mariaathens
- Lia 2006
- 1205
- παιδι για κλαματα
- Alexandros36k
- alexd99
- chembam
- Specon
- Dr House
- panagiotis23
- Johnman97
- rhymeasylum
- Αννα Τσιτα
- KaterinaL
- Libertus
- LeoDel
- iminspain
- den antexw allh apotyxia
- Λαμπρινηη
- Mendel2003
- Ijt
- drosos
- Κορώνα
- JohnGreek
- Αρχηγος_β3
- alexandra_
- ΘανάσοςG4
- Dimitris9
- Birtjan
- george7cr7
- NickT
- Bgpanos
- JKTHEMAN
- nicole1982
- χημεια4λαιφ
- Stroka
- Kostakis45
- charmander
- leo41
- EiriniS20
- Αριάνα123
- MarilynSt
- iManosX13
- Nefh_
- Viedo
- Βλα
- suaimhneas
- george pol
- kristinbacktoschool
- fearless
- Rene2004
- Steffie88
- Slytherin
- jimnikol21
- Unseen skygge
- cel123
- jul25
- Thanos_D
- Ireneeneri
- tasost
- Mukumbura
- xxxtolis
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki



