Συλλογή ασκήσεων και τεστ στα Μαθηματικά Προσανατολισμού

[DumeNuke]

Εστω συνάρτηση ορισμένη στο με
Να βρείτε τον τύπο της αν

Η αντιπαραγώγιση εδώ.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[nikoslarissa]

Να βρείτε τον γ.τ των μιγαδικών z για τους οποιους ισχυει

Ο a είναι πραγματικός

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[DumeNuke]

Να βρείτε τον γ.τ των μιγαδικών z για τους οποιους ισχυει

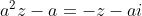
Ο a είναι πραγματικός

Λύση.

Edit: Συμπληρωματικη.
Ωραία και σύντομη λύση Ιάσωνα!

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[nikoslarissa]

Το ίδιο λάθος έκανα και εγώ όταν την πρωτοείδα βάλε για z=2-2i και θα φτάσεις σε μια δευτεροβάθμια εξίσωση με α που είναι αδύνατη.Η άσκηση είναι αρκετά πιο δύσκολη από όσο φαίνεται.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[IasonasM]

λύνοντας ως προς z έχεις :
z= a/(a² + 1) - a/(a² +1) i
άρα αν M(x,y) σημείο του γτ. <=> x= a/(a² + 1) και y = - a/(a² +1) <=> x=-y με -1/2<= x <= 1/2
Δηλαδή ο γτ. είναι η (ε): x+y=0 με -1/2 <= x <= 1/2
(ο περιορισμός του x προέκυψε από το σύνολο τιμών της f(x)= x/(x²+1) , x e R )

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[nikoslarissa]

λύνοντας ως προς z έχεις :
z= a/(a² + 1) - a/(a² +1) i
άρα αν M(x,y) σημείο του γτ. <=> x= a/(a² + 1) και y = - a/(a² +1) <=> x=-y με -1/2<= x <= 1/2
Δηλαδή ο γτ. είναι η (ε): x+y=0 με -1/2 <= x <= 1/2
(ο περιορισμός του x προέκυψε από το σύνολο τιμών της f(x)= x/(x²+1) , x e R )

Αυτή είναι η σωστή λύση

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Guest 018946]

κρετινε ειμαι ο κολικος ειμαι η καπνα της αθηνας .

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Αντικειμενικός]

Βοηθεια παιδια
Έχω μιγαδικο Z για τον οποίο ισχύει:
|(1-i) * Z -14+2i|=5√2.
i) να βρείτε τον γ.τ. των εικονων του z
ii) Να βρείτε την μέγιστη και την ελαχιστη τιμη καθώς και τους μιγαδικους των οποιων παριστανει τις τιμες αυτες.
iii) Αν z1,z2 μιγαδικοι του γεωμετρικου τοπου του ερωτηματος (i) να βρειτε την μεγιστη τιμη του |z1-z2|

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Civilara]

Βοηθεια παιδια
Έχω μιγαδικο Z για τον οποίο ισχύει:
|(1-i) * Z -14+2i|=5√2.
i) να βρείτε τον γ.τ. των εικονων του z
ii) Να βρείτε την μέγιστη και την ελαχιστη τιμη καθώς και τους μιγαδικους των οποιων παριστανει τις τιμες αυτες.
iii) Αν z1,z2 μιγαδικοι του γεωμετρικου τοπου του ερωτηματος (i) να βρειτε την μεγιστη τιμη του |z1-z2|

i) Θέτουμε z=x+yi όπου x,y ανήκουν R. Έχουμε:
(1-i)z-14+2i=(1-i)(x+yi)-14+2i=x+yi-xi+y-14+2i=(x+y-14)+(y-x+2)i
|(1-i)z-14+2i|=SQRT[((x+y-14)^2)+((y-x+2)^2)]
|(1-i)z-14+2i|^2=((x+y-14)^2)+((y-x+2)^2)=x^2+y^2+196+2xy-28x-28y+(y^2)+(x^2)+4-2xy+4y-4x=2(x^2)+2(y^2)-32x-24y+200

Έχουμε
|(1-i)z-14+2i|=5SQRT(2) => |(1-i)z-14+2i|^2=50 => 2(x^2)+2(y^2)-32x-24y+200=50 => 2(x^2)+2(y^2)-32x-24y+150=0 =>
=> (x^2)+(y^2)-16x-12y+75=0 => [(x^2)-16x+64]+[(y^2)-12y+36]=25 => ((x-4)^2)+((y-6)^2)=5^2 (1)

Επομένως ο z ανήκει σε κύκλο C με κέντρο Κ(4,6) και ακτίνα ρ=5.

ii) Έστω Α και Β τα σημεία στα οποία η ευθεία (ε) που διέρχεται από την αρχή Ο(0,0) και Κ(4,6) έτσι ώστε (ΟΑ)<(ΟΒ). Αν M(x,y) η εικόνα του z τότε ισχύει (ΟΑ)<=(ΟΜ)<=(ΟΒ) για κάθε Μ(z) ανήκει C. Αν A(z1) και B(z2) τότε η προηγούμενη σχέση γράφεται στη μορφή |z1|<=|z|<=|z2|. Συνεπώς min|z|=|z1| και max|z|=|z2|.

Η ευθεία (ε) έχει εξίσωση της μορφής y=αx+β. Επειδή διέρχεται από την αρχή Ο(0,0) τότε β=0, οπότε y=αx. Η (ε) διέρχεται από το σημείο Κ(4,6), οπότε οι συντεταγμένες του επαληθεύουν την εξίσωσή της:
6=α*4 => α=3/2

Συνεπώς η ευθεία (ε) έχει εξίσωση y=(3/2)x (2)

Οι συντεταγμένες των σημείων τομής της ευθείας (ε) με τον κύκλο C προκύπτουν από το σύστημα των δύο εξισώσεων. Αντικαθιστώντας την (2) στην (1) προκύπτει:

((x-4)^2)+((y-6)^2)=5^2 => ((x-4)^2)+(((3χ/2)-6)^2))=25 => ((x-4)^2)+(9/4)((χ-4)^2)=25 => (13/4)((χ-4)^2)=25 =>
=> ((χ-4)^2)=100/13 => |χ-4|=10/SQRT(13) => x-4=-10/SQRT(13) ή x-4=10/SQRT(13) => x=4-10/SQRT(13) ή x=4+10/SQRT(13)

Έχουμε:
x1=4-(10/SQRT(13))=4-(10SQRT(13)/13)=(52-10SQRT(13))/13
y1=(3/2)x1=(3/2)[4-(10/SQRT(13))]=6-(15/SQRT(13))=6-(15SQRT(13)/13)=(78-15SQRT(13))/13

x2=4+(10/SQRT(13))=4+(10SQRT(13)/13)=(52+10SQRT(13))/13
y2=(3/2)x2=(3/2)[4+(10/SQRT(13))]=6+(15/SQRT(13))=6+(15SQRT(13)/13)=(78+15SQRT(13))/13

Τα σημεία Α(x1,y1) και Β(x2,y2) είναι τα
Α((52-10SQRT(13))/13,(78-15SQRT(13))/13)
Β((52+10SQRT(13))/13,(78+15SQRT(13))/13)

Στη συνέχεια υπολογίζονται τα (ΟΑ) και (ΟΒ):
(ΟΑ)^2=(x1^2)+(y1^2)=[(4-(10/SQRT(13)))^2]+[(6-(15/SQRT(13)))^2]=16+(100/13)-(80/SQRT(13))+36+(225/13)-(180/SQRT(13))
(OA)^2=52+(325/13)-(260/SQRT(13))=52+25-(260/SQRT(13))=75-(260/SQRT(13))=75-20SQRT(13)

(ΟB)^2=(x2^2)+(y2^2)=[(4+(10/SQRT(13)))^2]+[(6+(15/SQRT(13)))^2]=16+(100/13)+(80/SQRT(13))+36+(225/13)+(180/SQRT(13))=52+(325/13)+(260/SQRT(13))=52+25+(260/SQRT(13))=75+(260/SQRT(13))=75+20SQRT(13)

Παρατηρούμε ότι όντως ισχύει (ΟΑ)<(ΟΒ).

Άρα
z1=x1+y1=[(52-10SQRT(13))/13]+[(78-15SQRT(13))/13]i με |z1|=75-20SQRT(13)
z2=x2+y2=[(52+10SQRT(13))/13]+[(78+15SQRT(13))/13]i με |z2|=75+20SQRT(13)

iii) Οι μιγαδικοί αριθμοί z1, z2 δεν είναι αυτοί που υπολογίστηκαν στο ερώτημα ii) αλλά είναι δύο τυχαίοι μιγαδικοί αριθμοί των οποίων οι εικόνες ανήκουν στον κύκλο C. Το μέτρο |z1-z2| της διαφοράς (z1-z2) παριστάνει το μήκος της χορδής του κύκλου με άκρα τις εκονές M1(z1) και M2(z2). Επειδή το ευθύγραμμο τμήμα Μ1Μ2 είναι χορδή του κύκλου τότε το μήκος της γίνεται μέγιστο όταν τα σημεία Μ1, Μ2 είναι αντιδιαμετρικά. Σε αυτήν την περίπτωση το ευθύγραμμο τμήμα Μ1Μ2 έχει μήκος ίσο με τη διάμετρο του κύκλου. Συνεπώς:

max|z1-z2|=2ρ=2*5=10

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Filippos14]

Παρε κοσμε
https://blogs.sch.gr/smichailog/files/2014/07/diagon_syn_oria.pdf

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[ΕλευθεριⒶκος]

Παρε κοσμε
https://blogs.sch.gr/smichailog/files/2014/07/diagon_syn_oria.pdf

Αυτος που το εφτιαξε ειναι καθηγητης στο σχολειο μου

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Guest 190013]

[f(x)]^3 + f(x) = x + 3

Να δείξετε (με γνώσεις μόνο από το πρώτο κεφάλαιο της ανάλυσης ) ότι f(x) συνεχής στο R

Για να σας δω.. Δεν είναι (πολύ) δύσκολη...

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[DumeNuke]

[f(x)]^3 + f(x) = x + 3

Να δείξετε (με γνώσεις μόνο από το πρώτο κεφάλαιο της ανάλυσης ) ότι f(x) συνεχής στο R

Για να σας δω.. Δεν είναι (πολύ) δύσκολη...

Λύση.

Βρήκα και μια δεύτερη λύση, πολύ πιο σύντομη (ειδικά άμα θεωρήσεις δεδομένη τη συνέχεια της αντίστροφης), αλλά δεν είμαι σίγουρος αν είναι σωστή.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[rebel]

Μία διαισθητικά απλή: Να δείξετε ότι δεν υπάρχει μιγαδικός αριθμός , τέτοιος ώστε .

Από εδώ

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Civilara]

Μία διαισθητικά απλή: Να δείξετε ότι δεν υπάρχει μιγαδικός αριθμός , τέτοιος ώστε .

Από εδώ

Η δική μου προσέγγιση είναι να βρω όλους τους μιγαδικούς αριθμούς z που είναι λύσεις της εξίσωσης |z-2|+|z+2|=4 και στη συνέχεια να αποδείξω ότι όλοι αυτοί είναι πραγματικοί αριθμοί.

Θέτω |z-2|=α, οπότε |z+2|=4-α ώστε |z-2|+|z+2|=4.
Επειδή |z-2|>=0 τότε α>=0
Επειδή |z+2|>=0 τότε 4-α>=0 => α<=4
Άρα 0<=α<=4

Αν α=0 τότε
|z-2|=0 => z-2=0 => z=2
|z-2|+|z+2|=0+4=4 που ισχύει
Άρα ο αριθμός z=2 είναι λύση της εξίσωσης

Αν α διάφορο 0 (0<α<=4), θέτουμε z=x+yi όπου x,y ανήκουν R. Έχουμε:
z-2=(x-2)+yi
z+2=(x+2)+yi

οπότε
|z-2|=α => |z-2|^2=α^2 => ((x-2)^2)+(y^2)=α^2
Άρα ο z ανήκει σε κύκλο με κέντρο Κ(2,0) και ακτίνα α. Οι παραμετρικές εξισώσεις αυτού του κύκλου είναι:
x=2+ασυνθ
y=αημθ
όπου 0<=θ<2π

Άρα
z=x+yi=(2+ασυνθ)+(αημθ)i
z-2=(x-2)+yi=(ασυνθ)+(αημθ)i
z+2=(x+2)+yi=(4+ασυνθ)+(αημθ)i

Έχουμε
|z+2|=4-α => |z+2|^2=(4-α)^2 => ((4+ασυνθ)^2)+((αημθ)^2)=(4-α)^2 => 16+8ασυνθ +(α^2)(συνθ^2)+(α^2)(ημθ^2)=16-8α+(α^2) => 16+8ασυνθ+(α^2)=16-8α+(α^2) => 8ασυνθ=-8α => (α διάφορο 0) συνθ=-1

Επειδή συνθ=-1 και 0<=θ<2π τότε θ=π με ημθ=0.

Επομένως
x=2+α*(-1)=2-α
y=α*0=0

οπότε
z=x+yi=(2-α)+0*I=2-α, 0<α<=4

Για α=0 στην παραπάνω σχέση προκύπτει z=2 που έχει βρεθεί ότι είναι λύση της εξίσωσης

Άρα
z=2-α, 0<=α<=4 ή αλλιώς
z=2-|z-2|, 0<=|z-2|<=4
που σημαίνει ότι όλες οι ρίζες της εξίσωσης είναι πραγματικοί αριθμοί.

Επειδή α=|z-2| τότε
z=2-|z-2| => |z-2|=2-z => |z-2|=-(z-2)

Αν θέσουμε w=z-2 <=> z=w+2 τότε η παραπάνω ανισότητα γίνεται |w|=-w <=> w=-|w|.
Επομένως ο w είναι πραγματικός αριθμός και ισχύει w<=0. Έχουμε:
w<=0 => z-2<=0 => z<=2

0<=|z-2|<=4 => -4<=-|z-2|<=0 => -2<=2-|z-2|<=2 => -2<=z<=2

Άρα οι μιγαδικοί αριθμοί z που είναι ρίζες της εξίσωσης |z-2|+|z+2|=4 είναι όλοι οι πραγματικοί αριθμοί στο διάστημα [-2,2]. Συνεπώς η εξίσωση αυτή δεν έχει λύσεις μιγαδικούς αριθμούς που να μην είναι πραγματικοί αριθμοί.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[blackorgrey]

Μία διαισθητικά απλή: Να δείξετε ότι δεν υπάρχει μιγαδικός αριθμός , τέτοιος ώστε .

Από εδώ

Ψάχνουμε τα σημεία των οποίων το άθροισμα των αποστάσεων από τα σημεία Α(2,0) Β(-2,0) είναι ίσο με την απόσταση ΑΒ.
Έστω ότι υπάρχει σημείο Μ εικόνα του z εκτός της ευθείας ΑΒ,τότε από τριγωνική ανισότητα καταλήγουμε σε άτοπο αφού σε κάθε περίπτωση θα ισχύει ΜΑ+ΜΒ>ΑΒ
Αν υποθέσουμε ότι το σημείο Μ βρίσκεται πάνω στην ευθεία ΑΒ αλλά εκτός του ευθυγράμμου τμήματος ΑΒ τότε ΜΒ=ΜΑ+ΑΒ>ΑΒ ή αντίστοιχα ΜΑ=ΑΒ+ΜΒ>ΜΒ το οποίο είναι άτοπο.
Άρα αφού για όλα τα σημεία Μ του ευθυγράμμου τμήματος ΑΒ και μόνο για αυτά ισχύει ΜΑ+ΜΒ=ΑΒ τότε αυτό το ευθύγραμμο τμήμα είναι ο γεωμετρικός τόπος των z το οποίο είναι τμήμα της ευθείας y=0,δηλαδή οι μιγαδικοί που ικανοποιούν τη σχέση είναι πραγματικοί
Αυτή είναι μια καθαρά γεωμετική λύση.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Guest 190013]

Λύση.

Βρήκα και μια δεύτερη λύση, πολύ πιο σύντομη (ειδικά άμα θεωρήσεις δεδομένη τη συνέχεια της αντίστροφης), αλλά δεν είμαι σίγουρος αν είναι σωστή.

Ενδιαφέρων ο 2ος τρόπος, εγώ την πρώτη φορά το έλυσα όπως στον πρώτο τρόπο καρμπόν. Όμως, το τελευταίο όριο το οποίο λες ότι ισούται με μηδέν, δεν είναι απολύτως ορθό, μου είχε πει ο καθηγητής μου, χωρίς να μου εξηγήσει τον λόγο (αν μπορεί κάποιος να μας διαφωτίσει εδώ). Η ορθότερη λύση, όπως μου είπε, είναι να πάρεις την παράσταση μέσα στο όριο, να φτιάξεις μια διπλή ανισότητα και να εφαρμόσεις κριτήριο παρεμβολής. Το δύσκολο είναι στο πώς φτιάχνεις την ανισότητα

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Filippos14]

Ενδιαφέρων ο 2ος τρόπος, εγώ την πρώτη φορά το έλυσα όπως στον πρώτο τρόπο καρμπόν. Όμως, το τελευταίο όριο το οποίο λες ότι ισούται με μηδέν, δεν είναι απολύτως ορθό, μου είχε πει ο καθηγητής μου, χωρίς να μου εξηγήσει τον λόγο (αν μπορεί κάποιος να μας διαφωτίσει εδώ). Η ορθότερη λύση, όπως μου είπε, είναι να πάρεις την παράσταση μέσα στο όριο, να φτιάξεις μια διπλή ανισότητα και να εφαρμόσεις κριτήριο παρεμβολής. Το δύσκολο είναι στο πώς φτιάχνεις την ανισότητα

Η λυση ειναι οντως λαθος,στο τελευταιο οριο ΔΕΝ μπωρεις να βαλεις οπου χ το χ0 καθως η συναρτηση f(x) δεν ξερεις αν ειναι συνεχης.Ουτε μπωρεις να σπασεις το οριο στο πηλικο γιατι δεν ξερεις αν υπαρχει το οριο του παρ/στη στο χ0.Η προσπαθεια λυσεις σταματαει στο τελευταιο οριο.
Αν εχεις το lim x->χ0 (g(x)/f(x)) και ας πουμε οτι η g ειναι συνεχης αλλα δεν ξερεις αν ειναι η f συνεχης ΔΕΝ μπωρεις να κανεις αμεση αντικατασταση,ουτε να σπασεις το οριο σε lim x->x0 (g(x))/lim x->x0 (f(x)),αυτο γιατι δεν ξερεις αν υπαρχει το οριο της f στο χ0,αν υπηρχε θα μπωρουσες.

Για να εγκλωβισεις την συναρτηση κανεις το εξης :
|f(x)-f(x0)|=|x-x0/(f^2(x)+f(x)f(x0)+f^2(x0)+1| <=| x-x0|("βγαζοντας τον παρονομαστη ουσιαστικα αυξανεις) απο δω η συνεχεια ειναι πολυ απλη.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Guest 190013]

Η λυση ειναι οντως λαθος,στο τελευταιο οριο ΔΕΝ μπωρεις να βαλεις οπου χ το χ0 καθως η συναρτηση f(x) δεν ξερεις αν ειναι συνεχης.Ουτε μπωρεις να σπασεις το οριο στο πηλικο γιατι δεν ξερεις αν υπαρχει το οριο του παρ/στη στο χ0.Η προσπαθεια λυσεις σταματαει στο τελευταιο οριο.
Αν εχεις το lim x->χ0 (g(x)/f(x)) και ας πουμε οτι η g ειναι συνεχης αλλα δεν ξερεις αν ειναι η f συνεχης ΔΕΝ μπωρεις να κανεις αμεση αντικατασταση,ουτε να σπασεις το οριο σε lim x->x0 (g(x))/lim x->x0 (f(x)),αυτο γιατι δεν ξερεις αν υπαρχει το οριο της f στο χ0,αν υπηρχε θα μπωρουσες.

Αυτό πρέπει να είναι, σωστός τώρα βέβαια την είπα λίγο πολύ τη λύση από δω και πέρα αλλά όποιος την έχει ας την ποστάρει

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Filippos14]

Αυτό πρέπει να είναι, σωστός τώρα βέβαια την είπα λίγο πολύ τη λύση από δω και πέρα αλλά όποιος την έχει ας την ποστάρει

Την ποσταρα δες το ποστ πανω

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.