Guest 018946
Επισκέπτης


Θεωρούμε τους μιγαδικούςτέτοιους ώστε
α) Να αποδειχθεί ότι
β) Να αποδειχθεί ότι δεν υπάρχουν μιγαδικοίμε τις παραπάνω ιδιότητες τέτοιοι ώστε
, όπου
οι εικόνες των
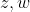
btw νομιζω οτι στον w εχεις κανει λαθος ενα προσημο στον αριθμητη πρεπει ναι ειναι +i
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 018946
Επισκέπτης


Ps: Περιμενω βαρυ υλικο

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 018946
Επισκέπτης


γιατι πολυ θα βολεβε

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
eimaimathitis
Νεοφερμένο μέλος


Αφού η
Έστω λοιπόν, ότι
Οπότε έχουμε:
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
IasonasM
Εκκολαπτόμενο μέλος


άρα αν έχει ρίζα r τότε r=1
για x=1 η αρχική : f(f(1))=a+b =>f(f(1))=1 => f(f(f(1)))=f(1) => af(1)+b=f(1) => (1-a)*f(1)=b => f(1)=1
άρα όντως η f(x)=x έχει μοναδική ρίζα την x=1.
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 018946
Επισκέπτης


βαζω οπου χ το φ(χ) στην αρχικη και εχω φ(αχ+β)=αφ(χ)+β
για χ=1 εχω φ(1)=1
αρα ειναι λυση της φ(χ)=χ αφου για χ=1 εχω φ(1)=1 <=> 1=1 που ισχυει
εστω οτι υπαρχει και χ0>1 ωστε φ(χ0)=χ0
τοτε βαζοντας οπου χ το χ0 στην αρχικη θα εδινε φ(φ(χ0))=αχ0+β
φ(χ0)=αχ0+β
χ0=αχ0+β
χ0=1
ατοπο
ομοια παιρνω ατοπο αν υποθεσω οτι χ0<1
και το ζητουμενο εχει αποδειχτει και μπορω να κοιμηθω ησυχος
https://www.youtube.com/watch?v=WY70W5C9VDk
το προβλημα στη λυση του ειμαιμαθητης φαστιστες κουφαλες ερχονται κρεμαλες ειναι οτι δεν ξερεις αμα η φ ειναι οντως πολύωνυμο
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
eimaimathitis
Νεοφερμένο μέλος


Εγώ είπα μεγαλύτερη μαλακία!
Πιο πριν έλυνα ασκήσεις με πολυωνυμικές συναρτήσεις και κόλλησε το μυαλό μου

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 018946
Επισκέπτης


ολοι θα τα καταφερουμε γαμω
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
xristospr
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


Για μία συνάρτησηισχύει
όπου
δύο δοσμένοι πραγματικοί αριθμοί με
και
. Να αποδείξετε ότι η εξίσωση
έχει μία μοναδική ρίζα στο
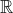
Επειδή α+β=1 τότε β=1-α και επειδή β διάφορο 0 τότε α διάφορο 1.
(i) Αν α=0 τότε β=1 και η σχέση γίνεται f(f(x))=1 για κάθε x ανήκει R. Αν η συνάρτηση f δεν είναι σταθερή τότε υπάρχουν x1, x2 με x1 διάφορο x2 ώστε f(x1) διάφορο f(x2). Τότε έχουμε:
f(x1) διάφορο f(x2) => f(f(x1)) διάφορο f(f(x2)) που είναι άτοπο αφού f(f(x1))=f(f(x2))=1
Άρα η f είναι σταθερή, δηλαδή υπάρχει c ανήκει R ώστε f(x)=c για κάθε x ανήκει R. Άρα f(f(x))=c και επειδή f(f(x))=1 για κάθε x ανήκει R τότε c=1 που σημαίνει ότι f(x)=1 για κάθε x ανήκει R.
f(x)=x => x=1
Άρα η εξίσωση f(x)=x έχει μοναδική ρίζα την x=1
(i) Αν α διάφορο 0 τότε επειδή β διάφορο 0 και β=1-α ισχύει α διάφορο 1. Άρα α ανήκει (-οο,0)U(0,1)U(1,+oo).
Ισχύει f(f(x))=αx+1-α, x ανήκει R
Θεωρούμε x1, x2 ανήκουν R με f(x1)=f(x2). Έχουμε
f(x1)=f(x2) => f(f(x1))=f(f(x2)) => αx1+1-α=αx2+1-α => αx1=αx2 => x1=x2
Άρα η f είναι 1-1.
Από την σχέση f(f(x))=αx+1-α, έχουμε:
f(f(f(x)))=f(αx+1-α), x ανήκει R
f(f(f(x)))=αf(x)+1-α, x ανήκει R
Άρα f(αx+1-α)=αf(x)+1-α για κάθε x ανήκει R
Για x=1 προκύπτει
f(α+1-α)=αf(1)+1-α => f(1)=αf(1)+1-α => αf(1)-f(1)+1-α=0 => (α-1)f(1)-(α-1)=0 => (α-1)(f(1)-1)=0 => f(1)-1=0 => f(1)=1 (α διάφορο 1)
Έστω η συνάρτηση g(x)=f(x)-x, x ανήκει R. Θεωρούμε x1, x2 με f(x1)=f(x2). Επειδή η f είναι 1-1 προκύπτει x1=x2. Από τις 2 τελευταίες σχέσεις προκύπτει f(x1)-x1=f(x2)-x2 => g(x1)=g(x2).
Επομένως η g είναι 1-1. Για x=1 έχουμε g(1)=f(1)-1=1-1=0
Άρα ο x=1 είναι ρίζα της g(x)=0 και επειδή η g είναι 1-1 τότε είναι και η μοναδική ρίζα της εξίσωσης g(x)=0 <=> f(x)=x.
Συνεπώς σε κάθε περίπτωση η εξίσωση f(x)=x έχει μοναδική λύση την x=1.
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Αν και είναι εκτός εποχής θα επιθυμούσα μία λύση σε αυτήνΑν η f είναι συνεχής στο [α,β], παραγωγίσιμη στο (α,β) και f(α)=f(β)=0, τότε να αποδειχθεί ότι υπάρχειτέτοιο ώστε:
 \right|\geq \frac{4}{{\left(\beta -\alpha \right)}^{2}}\int_{\alpha }^{\beta }\left|f(x) \right|dx)

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 018946
Επισκέπτης


Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


Αν και είναι εκτός εποχής θα επιθυμούσα μία λύση σε αυτήν
Η αλήθεια είναι Κώστα πως δεν την έχω καταφέρει και επειδή δεν έχω τη λύση της την ανάρτησα μήπως και τη λύσει κάποιος από τους μαθηματικούς ή οποιοσδήποτε χρήστης.
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


Να μία συγγενική που έχω βρει όπου η ανισότητα είναι λιγότερο ισχυρή και η λύση από έναν ολυμπιονίκη. Αν δεν κάνω λάθος χρησιμοποιεί Taylor. Ίσως σ'ενδιαφέρει.
Βρέθηκε η λύση.
Αν η f είναι σταθερή και επειδή f(α)=f(β)=0 τότε f(x)=0, x ανήκει [α,β] όποτε f΄(x)=0, x ανήκει (α,β). Σε αυτήν την περίπτωση για κάθε ξ ανήκει (α,β) ισχύει η ισότητα.
Λύθηκε η άσκηση.
Ο άνθρωπος αυτός είναι αστέρι.
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Μία μικρή. Έστω η συνεχής συνάρτησηΚωστα μπορεις να βαλεις καμια ασκηση απο αναλυση μεχρι Bolzano ξερω γω ;
Να αποδείξετε ότι η εξίσωση
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 018946
Επισκέπτης


λιμαρω στο + απειρο και στο - απειρο και βγαζω οτι το συνολο τιμων ( ειχα κανει και ενα κοινο παραγοντα το χ^2013) ειναι το R αρα θα υπαρχει τουλαχιστον ενα χ0 στο R ωστε να μηδενιζει αυτη η συναρτηση
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 0 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 288 μέλη διάβασαν αυτό το θέμα:
- 98.8%chimpanzee
- trifasikodiavasma
- ggl
- ioanna2007
- Hased Babis
- thepigod762
- akis_95
- Mariosm.
- Maynard
- infection54
- Jesse_
- topg
- eukleidhs1821
- bill09876
- Debugging_Demon
- mali
- Joji
- Ness
- Helen06
- Scandal
- synthnightingale
- arko
- BillyTheKid
- Magigi
- Paragontas7000
- Unboxholics
- just some guy
- george777
- Wonderkid
- IceCream05
- Abiogenesis
- GeorgePap2003
- katia.m
- giannhs2001
- paul
- Praxis
- Apocalypse
- shezza94
- desp1naa
- rempelos42
- Sherlockina
- oups
- Dimgeb
- spring day
- KingOfPop
- mpapa
- Chrisa
- Physicsstudent
- tsiobieman
- P.Dam.
- persi
- theodoraooo
- PanosBat
- kost28
- mikriarchitectonissa
- BILL KEXA
- Dr. Gl. Luminous
- Eleftheria2
- Athens2002
- bruh_234
- Miranda32
- SlimShady
- kallikd
- nucomer
- alpha.kappa
- Eeeee
- J.Cameron
- Marple
- Kitana
- F1L1PAS
- sophiaa
- VFD59
- papa2g
- το κοριτσι του μαη
- srg96
- Hopeful22
- Φινεύς
- Phys39
- Anta2004
- fairyelly
- Pharmacist01
- jYanniss
- Panagiotis849
- Kokro
- augustine
- Nikoletaant
- Mashiro@Iberan
- margik
- Mammy Nun
- Pastramis
- Σωτηρία
- Appolon
- panosveki
- Nickt23
- igeorgeoikonomo
- Steliosgkougkou
- QWERTY23
- Ameliak
- aladdin
- nimbus
- Φωτεινη Τζα.
- marian
- Georgekk
- xrisamikol
- the purge
- Theodora03
- Machris
- s93060
- Nikitas18
- Stif6
- stav.mdp
- damn
- aekaras 21
- Anthropaki
- Angelos12345
- ioannam
- Μάρκος Βασίλης
- skyway
- Nick2325
- Nala
- Manolo165
- Ryuzaki
- T C
- Devilshjoker
- El_
- George9989
- TonyMontanaEse
- globglogabgalab
- constansn
- barkos
- katerinavld
- fenia
- An_uknown_world
- Jimmis18
- maria2001
- KingPoul
- Xara
- thecrazycretan
- abcdefg12345
- Κλημεντίνη
- ale
- panagiotis G
- mechaniceng
- Giii
- calliope
- Tequila
- natalix
- Cortes
- Alexecon1991
- pepsoula
- Mariaathens
- Lia 2006
- 1205
- παιδι για κλαματα
- Alexandros36k
- alexd99
- chembam
- Specon
- Dr House
- panagiotis23
- Johnman97
- rhymeasylum
- Αννα Τσιτα
- KaterinaL
- Libertus
- LeoDel
- iminspain
- den antexw allh apotyxia
- Λαμπρινηη
- Mendel2003
- Ijt
- drosos
- Κορώνα
- JohnGreek
- Αρχηγος_β3
- alexandra_
- ΘανάσοςG4
- Dimitris9
- Birtjan
- george7cr7
- NickT
- Bgpanos
- JKTHEMAN
- nicole1982
- χημεια4λαιφ
- Stroka
- Kostakis45
- charmander
- leo41
- EiriniS20
- Αριάνα123
- MarilynSt
- iManosX13
- Nefh_
- Viedo
- Βλα
- suaimhneas
- george pol
- kristinbacktoschool
- fearless
- Rene2004
- Steffie88
- Slytherin
- jimnikol21
- Unseen skygge
- cel123
- jul25
- Thanos_D
- Ireneeneri
- tasost
- Mukumbura
- xxxtolis
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

