Προσπάθησα να κάνω την απόδειξη όσο πιο απλή γίνεται και από τι κατάλαβα έχεις κάποιες απορίες.
Γι' αυτό θα ξεκινήσω με μια χαρακτηριστική πρόταση η οποία για να κατανοηθεί χρειάζεται να έχεις κατανοήσει τον ορισμό

του ορίου της συνέχειας και της παραγώγου.Xωρίς να λες για παράδειγμα προτάσεις τύπου ''κοντά στο
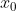
όταν αναφαίρεσαι σε όριο.
Πρόταση
Έστω μια συνάρτηση f: Deltarightarrow R που στο
εσωτερικό σημείο

είναι παραγώγηση.
(α) Αν
 >0)
, τότε υπάρχει περιοχή
subset Delta )
τέτοια,ώστε για κάθε
)
με

να ισχύει
<f(xi ) <f({x}_{2}))
.
(β) Αν
 <0)
, τότε υπάρχει περιοχή
subset Delta)
τέτοια,ώστε για κάθε
)
με

να ισχύει
>f(xi ) >f({x}_{2}))
.
Απόδειξη
Επειδή
-f(xi )}{x-xi }=f '(xi )>0)
υπάρχει

τέτοιο, ώστε για κάθε

με

να ισχύει
-f(xi )}{x-xi }>0 )
.
Επομένως, για

ισχύει
-f(xi )<0)
, δηλαδή
<f(xi ))
, ενώ για

ισχύει
-f({x}_{2})<0)
,δηλαδή
<f({x}_{2}))
.
Όμοια αποδεικνύεται το (β).
Σε ανάλογο κλίμα βάση του αυστηρού ορισμού του ορίου συνάρτης θα γίνει η απόδειξη του θεωρήματος των ενδιαμέσων τιμώς της παραγώγου
Θεώρημα Darboux ή θεώρημα ενδιάμεσης τιμής της παραγώγου:
Αν μια συνάρτηση
είναι παραγωγίσιμη στο διάστημα
,τότε (η παράγωγος της)
παίρνει όλες τις τιμές μεταξύ
και
, δηλαδή το
είναι διάστημα.
Aπόδειξη
Yποθέτουμε
>f '(beta ))
και
>lambda >f '(beta ))
. Θα αποδείξουμε ότι υπάρχει
)
τέτοιο, ώστε
=lambda)
.
Θεωρούμε τη συνάρτηση
,τότε η
είναι συνεχής στο

οπότε σύμφωνα με το θεώρημα Μεγίστου-Ελαχίστου(Extreme Value Theorem) η
παίρνει μια μέγιστη τιμή.Θα αποδείξουμε ότι

.
Eπειδή
>lambdaRightarrow f '(alpha )-lambda >lambda-lambda Rightarrow g '(alpha )>0)
, τότε σύμφωνα με την παραπάνω πρόταση υπάρχει

(ή περιοχή
)
κέντρου

ακτίνας

) ώστε για κάθε
)
να ισχύει
>g(alpha ))
. Aυτό όμως σημαίνει ότι η
)
δεν είναι η μέγιστη τιμή της
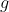
.
Ανάλογα αποδεικνύεται ότι

.
Eπομένως
)
και σύμφωνα με το θεώρημα Fermat ισχύει
=f '(xi )-lambda =0)
, δηλαδή
=lambda)
Ανάλογα αποδεικνύεται για
< f '(beta ))
Αν κατάλαβα σωστά μάλλον κάνεις λάθος διότι το θεώρημα Fermat ισχύει ΜΟΝΟ για εσωτερικά σημεία, με το να λέμε :

σημείο τοπικού ακροτάτου
=0)
.
είναι σα να λέμε
neq 0 Rightarrow )

σημείο τοπικού ακροτάτου .
Όμως οι παρακάτω ισχυρισμοί είναι αληθείς μόνο όταν το

είναι εσωτερικό σημείο. Επομένως με το να αποδεικνύεις ότι η παράγωγος στο άκρο ενός διαστήματος είναι διάφορη του μηδενός δε σου εξασφαλίζει ότι στο συγκεκριμένο σημείο η συνάρτηση δεν παρουσιάζει τοπικό ακρότατο γι' αυτό δουλεύουμε με το πρόσημο.




 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki















