Δυο απο τα Σ-Λ:
α) Αν f συνεχής στο [α,β] και f(α)f(β)>0 τοτε η
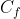
δεν τετμνει τον x'x
β) Αν f παραγωγισιμη στο 2 τότε
=[f(2)]' ) Θέμα 2ο
Θέμα 2ο
Έστω
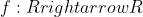
συνεχής και
-1}{{x}^{2}-1}=2 )
α) Δείξτε ότι f(1)=1
β) Δείξτε οτι f'(1)=4
γ) Αν f(2)=f(3)=7 δείξτε οτι η ευθεία y=4x-3 εχει ενα τουλαχιστον κοινό σημειο με την
 Θέμα 3ο
Θέμα 3ο
Έστω

η οποία ειναι συνεχής και παρουσιαζει ολικο ελαχιστο μόνο για x=1 το f(1)=3 και ολικό μεγιστο μόνο για x=2 το f(2)=5
α) Να βρείτε το συνολο τιμών της f
B) Δείξτε οτι υπαρχει
:f({x}_{0})=f(0) )
γ) Αν η f γνησιως μονοτονη σε καθενα απο τα διαστηματα [0,1] και [1,2] τότε:
i) Προσδιοριστε το ειδος μονοτονιας της f σε καθένα απο τα παραπανω διαστηματα
ii) Αν f(0)=4 βρείτε το πλήθος των ριζων της εξίσωσης f(x)=α για τις διαφορες τιμες του αεR
Θέμα 4ο
Α) Έστω συναρτηση f συνεχής και μη σταθερή στο R
α) Δείξτε οτι υπαρχει ενα τουλαχιστον
=frac{f(-1)+f(0)+f(1)}{3} )
β) Αν για την f ισχύουν f(0)>0 και
}]^{2}=2xf(x)+1 )
για καθε xεR, δειξτε οτι η g(x)=x διατηρεί σταθερό πρόσημο στο R και βρειτε τον τυπο της f
Β) Μια συναρτηση
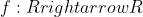
είναι παραγωγίσιμη και γνησίως μονοτονη με f(x)=-f(2-x) για καθε xεR
Αν
neq 0 )
για καθε xεR και η f' ειναι συνεχής τότε:
α) Να λυθεί η εξίσωση f(x)=0
β) Δείξτε οτι για την συναρτηση g με
=frac{f(x)}{f'(x)} )
ισχύει g'(1)=1
ΚΑΛΗ ΕΠΙΤΥΧΙΑ


 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki




 καμία
καμία
