
21-11-08

15:06
α)
(z_1^2+z_1z_2+z_2^2) = 0 \Leftrightarrow \\ z_1^3-z_2^3 = 0 \Leftrightarrow \\ z_1^3=z_2^3 )
β)
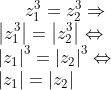
άρα (ΟΑ) = (ΟΒ) δηλαδή το ΟΑΒ είναι ισοσκελές
γ)
^2+\left( \frac{z_2}{z_1}\right)^2= \frac{z_1^2}{z_2^2}+\frac{z_2^2}{z_1^2} = \frac{z_1^4+z_2^4}{z_1^2z_2^2}=\frac{z_1^3z_1+z_2^3z_2}{z_1^2z_2^2} \\ =\frac{z_2^3z_1+z_1^3z_2}{z_1^2z_2^2}=\frac{z_1z_2(z_2^2+z_1^2)}{z_1^2z_2^2}=\frac{z_2^2+z_1^2}{z_1z_2}=\frac{-z_1z_2}{z_1z_2}=-1 )
ή
^2 =(-1)^2 \Leftrightarrow \\ \left( \frac{z_1}{z_2}\right)^2+2+\left( \frac{z_2}{z_1}\right)^2=1 \Leftrightarrow \\ \left( \frac{z_1}{z_2}\right)^2+\left( \frac{z_2}{z_1}\right)^2= -1)
δ)
^2 = z_1z_2 \Rightarrow \\ \left|z_1+z_2\right|^2 = \left|z_1\right| \left|z_2\right| \Leftrightarrow \\ \left|z_1+z_2\right|^2 = \left|z_1\right|^2 \Leftrightarrow \\ \left|z_1+z_2\right| = \left|z_1\right| \Leftrightarrow \\ \left|z_1+z_2\right| = \left|z_1\right|= \left|z_2\right|\Leftrightarrow \\ \left|z_1+z_2\right| = \left|z_1\right|= \left|(z_1+z_2)-z_1\right|)
άρα (OΓ) = (ΟΑ) = (ΑΓ) δηλαδή το ΟΑΓ είναι ισόπλευρο.
β)
άρα (ΟΑ) = (ΟΒ) δηλαδή το ΟΑΒ είναι ισοσκελές
γ)
ή
δ)
άρα (OΓ) = (ΟΑ) = (ΑΓ) δηλαδή το ΟΑΓ είναι ισόπλευρο.
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki
 !
!


