Συλλογή ασκήσεων και τεστ στα Μαθηματικά Προσανατολισμού

Civilara · 09-07-09

Ωραία τα σημερινά θεματάκια. Πιο δύσκολα από τα αντίστοιχα της κανονικής περιόδου αλλά χωρίς υπερβολές. Οι εκφωνίσεις με την πρώτη ανάγνωση ίσως να τρομοκρατούσαν αλλά ένας καλός και κυρίως ψύχραιμος μαθητής δεν είχε λόγο να φοβάται. Τα θέματα των επαναληπτικών εξετάσεων στα μαθηματικά κατεύθυνσης θα τα χαρακτήριζα θέματα "ψυχολογίας" περισσότερο παρά δύσκολα.

manos66 · 09-07-09

Απαντήσεις
View attachment mathkat_epan_09_a.pdf

\pi · 09-07-09

Το άπειρο στο latex γράφεται \infty

galois01 · 09-07-09

Αρχική Δημοσίευση από theodora:
αν ${z}_{1},{z}_{2}$ e C και ισχυει ${z}^{2}={z}_{1}{z}_{2}$ να δειξετε οτι $left|{z}_{1} right|+left|{z}_{2} right|=left|frac{{z}_{1}+{z}_{2}}{2}+z right|+left| frac{{z}_{1}+{z}_{2}}{2}-zright|$

sorry παιδια!δεν το εμαθα καλα,ετσι ειναι!

Αν $z_{2}=0$ τότε από τη σχέση $z^{2}=z_{1}z_{2}$ έχουμε $z=0$

Επομένως με αντικατάσταση βλέπουμε πως το ζητούμενο προφανώς ισχύει.

Για $z_{2}\neq0$ από την υπόθεση έχουμε

$z_{1}=\frac{z^{2}}{z_{2}}$ επομένως με αντικατάσταση το

δεύτερο μέλος γράφεται

$|\frac{z^{2}+z_{2}^{2}}{2z__2}}+z|+|\frac{z^{2}+z_{2}^{2}}{2z_{2}}-z|=\frac{|z+z_{2}|^{2}+|z-z_{2}|^{2}}{2|z_{2}|}$ και αναπτύσσοντας τα τετράγωνα έχουμε

$\frac{|z|^{2}+|z_{2}^{2}|}{|z_{2}|}=|\frac{z^{2}}{z_{2}}|+|z_{2}|=|z_{1}|+|z_{2}|$

οπότε το ζητούμενο έχει αποδειχθεί.

Κώστας

edit:Ευχαριστώ τον manos66 για την επισύμανση του τυπογραφικού λάθους.

Boom · 09-07-09

αν ειναι ${n}_{1},{n}_{2}$ ανηκει C νδο
$\left|{n}_{1}-n \right|+\left|{n}_{1}+n \right|=\left|{n}_{1}-{n}_{2} \right|+\left|{n}_{1}+{n}_{2} \right|$ οπου
${n}^{2}={{n}_{1}}^{2}-{{n}_{2}}^{2}$

kvgreco · 10-07-09

Νομίζω ότι στις επαναληπτικές το γελοιοποίησαν ακόμη περισσότερο.Κανένα "κρίσιμο" σημείο δεν περιέχουν οι ασκήσεις.Ειδικά στο τέταρτο όποιος είχε την υπομονή απλά να κάνει πράξεις ήταν οκ.Μιλάμε ότι αυτά αφορούν μαθητές που απλά είχαν κατανοήσει τα βασικά.
Καλά το τελευταίο ερώτημα(ορισμένο ολοκλήρωμα) γιατί το έβαλαν?Γιά ψάρωμα?Στο όρος πατάτα?
Καί να φανταστείτε ότι δεν είμαστε πιά σε προεκλογική περίοδο(ή μήπως είμαστε?)
Συνάντησα πρόσφατα ένα καθηγητή μου ο οποίος μού είπε ότι κατά 90% η ευκολία των φετινών θεμάτων έχει να κάνει με λόγους πολιτικούς.Εκεί φτάσαμε.
Τα πάντα στην υπηρεσία της σκοπιμότητας.

edit:
Το μόνο ερώτημα που κάπως μπορούσε να φοβίσει σε πρώτη ανάγνωση,είναι αυτό με την εξίσωση f(x)+a^2=0 το οποίο μοιάζει ελαφρώς με το περσινό ερώτημα τού τρίτου ζητήματος αλλά είναι σαφώς πιό εύκολο λόγω της μονοτονίας τη f.

Civilara · 10-07-09

Αρχική Δημοσίευση από kvgreco:
Νομίζω ότι στις επαναληπτικές το γελοιοποίησαν ακόμη περισσότερο.Κανένα κρίσιμο σημείο δεν περιέχουν οι ακσήσεις.Ειδικά στο τέταρτο όποιος είχε την υπομονή απλά να κάνει πράξεις ήταν οκ.
Καλά το τελευταίο ερώτημα(ορισμένο ολοκλήρωμα) γιατί το έβαλαν?Γιά ψάρωμα?Στο όρος πατάτα?
Καί να φανταστείτε ότι δεν είμαστε πιά σε προεκλογική περίοδο(ή μήπως είμαστε?)
Συνάντησα πρόσφατα ένα καθηγητή μου ο οποίος μού είπε ότι κατά 90% η ευκολία των φετινών θεμάτων έχει να κάνει με λόγους πολιτικούς.Εκεί φτάσαμε.
Τα πάντα στην υπηρεσία της σκοπιμότητας.

Δεν τίθεται θέμα ότι παίχτηκε πολιτικό παιχνίδι στις πλάτες των υποψηφίων. Είμαι σίγουρος (αλλά δεν μπορώ να το αποδείξω).

chris_90 · 10-07-09

Ιδιου επιπεδου με τα θεματα του Μαιου θα ελεγα. Το 4ο θεμα με "ψαρωσε" με την πρωτη ματια, αλλα τελικα ειχα κανει απειρες παρομοιες ασκησεις ολη τη χρονια. Οπως και οταν ειχα δει το 4ο οταν εγραφα ειχα μεινει να το κοιταζω κανα 5λεπτο, αλλα τελικα δεν ηταν κατι δυσκολο.

rolingstones · 10-07-09

Αρχική Δημοσίευση από kvgreco:
Νομίζω ότι στις επαναληπτικές το γελοιοποίησαν ακόμη περισσότερο.Κανένα "κρίσιμο" σημείο δεν περιέχουν οι ασκήσεις.Ειδικά στο τέταρτο όποιος είχε την υπομονή απλά να κάνει πράξεις ήταν οκ.Μιλάμε ότι αυτά αφορούν μαθητές που απλά είχαν κατανοήσει τα βασικά.
Καλά το τελευταίο ερώτημα(ορισμένο ολοκλήρωμα) γιατί το έβαλαν?Γιά ψάρωμα?Στο όρος πατάτα?
Καί να φανταστείτε ότι δεν είμαστε πιά σε προεκλογική περίοδο(ή μήπως είμαστε?)
Συνάντησα πρόσφατα ένα καθηγητή μου ο οποίος μού είπε ότι κατά 90% η ευκολία των φετινών θεμάτων έχει να κάνει με λόγους πολιτικούς.Εκεί φτάσαμε.
Τα πάντα στην υπηρεσία της σκοπιμότητας.

edit:
Το μόνο ερώτημα που κάπως μπορούσε να φοβίσει σε πρώτη ανάγνωση,είναι αυτό με την εξίσωση f(x)+a^2=0 το οποίο μοιάζει ελαφρώς με το περσινό ερώτημα τού τρίτου ζητήματος αλλά είναι σαφώς πιό εύκολο λόγω της μονοτονίας τη f.

μα απο την πρωτη στιγμη ελεγα οτι ειναι προεκλογικα τα θεματα αλλα εσεις λεγατε δεν εχουν σχεση με την πολιτικη οι πανελληνιες.καλα αυτο με το f(x)=-a^2 καμια σχεση με το περσινο που ειχε 3000 περιπτωσεις ενω αυτο ηταν προφανες αφου η φ ηταν γνησιως αυξουσα και δεν αλλαζε η μονοτονια τι αλλο μπορουσαν να κανουν για να τους βοηθησουν

Zod · 10-07-09

Ίδιας δυσκολίας με τα ημερήσια.

galois01 · 11-07-09

Αρχική Δημοσίευση από theodora:
αν ειναι ${n}_{1},{n}_{2}$ ανηκει C νδο
$left|{n}_{1}-n right|+left|{n}_{1}+n right|=left|{n}_{1}-{n}_{2} right|+left|{n}_{1}+{n}_{2} right|$ οπου
${n}^{2}={{n}_{1}}^{2}-{{n}_{2}}^{2}$

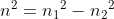
Υψώνωντας και τα δύο μέλη στο τετράγωνο και κάνοντας τις πράξεις έχουμε διαδοχικά

$|n|^{2}+|n_{1}-n||n_{1}+n|=|n_{2}|^{2}+|n_{1}-n_{2}||n_{1}+n_{2}|\Longleftrightarrow$

$|n|^{2}+|n_{1}^{2}-n^{2}|=|n_{2}|^{2}+|n_{1}^{2}-n_{2}^{2}|$

Aπό τη σχέση της υπόθεσης όμως η τελευταία προφανώς ισχύει άρα ισοδύναμα και η αρχική μας σχέση.

χρηστοσ17 · 17-07-09

f(x)=ln(1-lnx)

νδο ειναι γνησια φθινουσα

Chartson · 17-07-09

Αρχική Δημοσίευση από χρηστοσ17:
f(x)=ln(1-lnx)

νδο ειναι γνησια φθινουσα

θεωρώ χ1 ,χ2 που ανηκουν στο π.ο. με χ1<χ2 ,ln(χ1)<ln(χ2), -ln(x1)>-ln(x2), 1-ln(x1)>1-ln(x2) ,ln(1-ln(x1))>ln(1-ln(x2)) επομένως f(x1)>f(x2) me o<x<e (με τις παραγώγους γίνεται κόλαση)άρα με ορισμό

nikos0712 · 22-07-09

Αρχική Δημοσίευση από χρηστοσ17:
f(x)=ln(1-lnx)

νδο ειναι γνησια φθινουσα

πρωτα απο ολα χ<e σαν πεδιο ορισμου
εστω k(x)=lnx
για καθε χ<e η k ειναι γν. αυξ.
εστω g(x)=1-lnx
για καθε χ<e ειναι g'(x)=-1/χ<0 άρα η g ειναι γν. φθινουσα
αρα η f ειναι γν. φθ. σαν συνθεση μιας γν.αυξ. απο μια γν.φθ. *
*πορισμα απο ασκηση του σχολικου βιβλιου :jumpy:

-----------------------------------------
α......κ χ>0 αρα Df=(o,e)

kvgreco · 22-07-09

Άσκηση
Μιά άσκηση που μού έβαλε πρωτοετής φοιτητής στούς ΗΜΜΥ που τους την έβαλε ο καθηγητής τους.

Αν η πολυωνυμική συνάρτηση $f(x)$ έχει όλες τις ρίζες της πραγματικές και απλές, να αποδείξετε ότι η συνάρτηση ${(f'(x))}^{2}-f(x)f''(x)$ δεν έχει πραγματικές ρίζες.

galois01 · 23-07-09

Αρχική Δημοσίευση από kvgreco:
Άσκηση
Μιά άσκηση που μού έβαλε πρωτοετής φοιτητής στούς ΗΜΜΥ που τους την έβαλε ο καθηγητής τους.

Αν η πολυωνυμική συνάρτηση $f(x)$ έχει όλες τις ρίζες της πραγματικές και απλές, να αποδείξετε ότι η συνάρτηση ${(f'(x))}^{2}-f(x)f''(x)$ δεν έχει πραγματικές ρίζες.

Θεωρούμε την πολυωνυμική συνάρτηση $f(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+\dots+a_{1}x+a_{0}$ αν $p_{1},p_{2},\dots,p_{n}$ είναι οι ρίζες της τότε γράφεται

$f(x)=a_{n}(x-p_{1})(x-p_{2})\dots(x-p_{n})$

επομένως η παράγωγος της θα είναι

$f'(x)=a_{n}(x-p_{2})\dots(x-p_{n})+a_{n}(x-p_{1})(x-p_{3})\dots(x-p_{n})+\dots+a_{n}(x-p_{1})(x-p_{2})\dots(x-p_{n-1})$

Έτσι έχουμε

$\frac{f'(x)}{f(x)}=\frac{1}{x-p_{1}}+\frac{1}{x-p_{2}}+\dots+\frac{1}{x-p_{n}}$ για κάθε $x\neq\ p_{1},p_{2},\dots,p_{n}$

Παραγωγίζοντας την τελευταία σχέση έχουμε

$\frac{f''(x)f(x)-(f'(x))^{2}}{(f(x))^{2}}=-\frac{1}{(x-p_{1})^{2}}-\dots-\frac{1}{(x-p_{n})^{2}}<0$

επομένως $f''(x)f(x)-(f'(x))^{2}<0$ (1)

για κάθε $x\neq\ p_{1},p_{2},\dots,p_{n}$

Όμως από τον τύπο της παραγώγου έχουμε ότι $f'(x)\neq0$

για κάθε $x= p_{1},p_{2},\dots,p_{n}$ επομένως η (1) ισχύει για κάθε $x\in\mathbb{R}$ άρα το ζητούμενο έχει αποδειχθεί αφού

$(f'(x))^{2}-f''(x)f(x)>0$ για κάθε $x\in\mathbb{R}$

Κώστας

kvgreco · 23-07-09

Αρχική Δημοσίευση από galois01:
Θεωρούμε την πολυωνυμική συνάρτηση $f(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+dots+a_{1}x+a_{0}$ αν $p_{1},p_{2},dots,p_{n}$ είναι οι ρίζες της τότε γράφεται

$f(x)=a_{n}(x-p_{1})(x-p_{2})dots(x-p_{n})$

επομένως η παράγωγος της θα είναι

$f'(x)=a_{n}(x-p_{2})dots(x-p_{n})+a_{n}(x-p_{1})(x-p_{3})dots(x-p_{n})+dots+a_{n}(x-p_{1})(x-p_{2})dots(x-p_{n-1})$

Έτσι έχουμε

$frac{f'(x)}{f(x)}=frac{1}{x-p_{1}}+frac{1}{x-p_{2}}+dots+frac{1}{x-p_{n}}$ για κάθε $xneq p_{1},p_{2},dots,p_{n}$

Παραγωγίζοντας την τελευταία σχέση έχουμε

$frac{f''(x)f(x)-(f'(x))^{2}}{(f(x))^{2}}=-frac{1}{(x-p_{1})^{2}}-dots-frac{1}{(x-p_{n})^{2}}<0$

επομένως $f''(x)f(x)-(f'(x))^{2}<0$ (1)

για κάθε $xneq p_{1},p_{2},dots,p_{n}$

Όμως από τον τύπο της παραγώγου έχουμε ότι $f'(x)neq0$

για κάθε $xneq p_{1},p_{2},dots,p_{n}$ επομένως η (1) ισχύει για κάθε $xinmathbb{R}$ άρα το ζητούμενο έχει αποδειχθεί αφού

$(f'(x))^{2}-f''(x)f(x)>0$ για κάθε $xinmathbb{R}$

Κώστας

Μήπως στο τέλος αντί να λες γιά κάθε x διάφορο των ρ1,ρ2,....,ρν θέλεις να πείς ίσον ?

galois01 · 23-07-09

Αρχική Δημοσίευση από kvgreco:
Μήπως στο τέλος αντί να λες γιά κάθε x διάφορο των ρ1,ρ2,....,ρν θέλεις να πείς ίσον ?

Εχεις δίκιο ίσον ήθελα να γράψω, μπευρδεύτικα με το απο πάνω. Πάντως δεν νομίζω να δημιουργήθηκε πρόβλημα διότι είναι προφανές αυτό που ήθελα να γράψω.

kvgreco · 24-07-09

Αρχική Δημοσίευση από galois01:
Εχεις δίκιο ίσον ήθελα να γράψω, μπευρδεύτικα με το απο πάνω. Πάντως δεν νομίζω να δημιουργήθηκε πρόβλημα διότι είναι προφανές αυτό που ήθελα να γράψω.

Όχι ρε συ Κώστα κανένα πρόβλημα.Γιά κάποιον που έχει μιά ιδέα απ' αυτά όχι, αλλά αν είναι κάποιος που δεν τα έχει ξεκαθαρίσει καλά, μπορεί να τον μπέρδευε λίγο.
Πάντως πολύ υπομονή έχετε μερικοί και κάνετε ...θαύματα με το Latex.
Εγώ δεν είμαι τόσο υπομονετικός.

coheNakatos · 24-07-09

Αν και εχει περασει καιρος και πλεον δεν τον ενδιαφερει το τεστ και οι απαντησεις ομως ειναι εξασκηση για μενα ... θελω να το δει καποιος και να με διορθωσει .Ευχαριστω https://www.ischool.gr/attachment.php?attachmentid=622&d=1234039145 <---- το τεστ

Θεμα 1ο : Υψωνοντας στο τετραγωνο και κανοντας τις γνωστες ιδιοτητες , και ακομη θετοντας $z=x+yi$ εχουμε το ζητουμενο και για το ii) |z|min = α => |z|min = 1

Θεμα 2ο : ειναι : $|z|=1 (1)$ βαζοντας μετρο στην δεδομενη σχεση και χρησιμοποιοντας την (1) εχουμε την μεσοκαθετο Ε.Τ με ακρα τα Α(1,2) Β(3,4) και βρισκουμε την ευθεια ..

Θεμα 3ο :
$(1+i)z+(1+i)\bar{z}+4 =0 \Leftrightarrow |1+i| |z+\frac{4}{1+i}|=|1-i||z|\Leftrightarrow |z+2-2i|=|z|$ θετοντας παιρνουμε την ευθεια ε : $x-y+2=0$

$|z-w|min = |d(K,\epsilon)-\rho | \Leftrightarrow |z-w|min=2\sqrt{2}-1$

αρα $|z-w|\succeq 2\sqrt{2}-1$

Θεμα 4ο :

i) $F(z) = \frac{1-{|z|}^{2}}{{|1+iz|}^{2}} - \frac{2Re(z)i}{{|1+iz|}^{2}}<br />$ Κανοντας πραξεις και αφου $2Re(z) = z+\bar{z}$

φτανουμε στο ζητουμενο

ii) για το ξεκιναω α) ξεκιναω απο $F(z)= \bar{F(z)}$

Και κανοντας πραξεις κατεληξα $z=-\bar{z}$ αρα ο γ.τ ειναι ο αξονας των φανταστικων $x=0$ αλλα εχω τον περιορισμο $z\neq i$ αρα αν Μ(x,y) ο γ.τ πρεπει $M\neq (0,1)$ .Αρα ειναι ο αξονας y'y χωρις το σημειο Μ(0,1)

β) $F(z)=-\bar{F(z)}$ κανοντας πραξεις ... ${|z|}^{2} =1$ αρα επισης ο κυκλος με Κ(0,0) και ρ=1 εκτος του Μ(0,1)

Συλλογή ασκήσεων και τεστ στα Μαθηματικά Προσανατολισμού

Περιβόητο μέλος

Εκκολαπτόμενο μέλος

Νεοφερμένο μέλος

Νεοφερμένο μέλος

Επιφανές μέλος

Εκκολαπτόμενο μέλος

Περιβόητο μέλος

Διάσημο μέλος

Πολύ δραστήριο μέλος

Δραστήριο μέλος

Νεοφερμένο μέλος

Νεοφερμένο μέλος

Εκκολαπτόμενο μέλος

Εκκολαπτόμενο μέλος

Εκκολαπτόμενο μέλος

Νεοφερμένο μέλος

Εκκολαπτόμενο μέλος

Νεοφερμένο μέλος

Εκκολαπτόμενο μέλος

Δραστήριο μέλος