ledzeppelinick
Πολύ δραστήριο μέλος



Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
ledzeppelinick
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
manos66
Εκκολαπτόμενο μέλος


αχχχ.. με προλαβε ο βασιλης για την πρωτη... πολυ σωστος ο φιλος απο ροδο νομιζω και για την δευτερη!! οπως και να χει ανεβαζω την 1η πολυ αναλυτικα
To μόνο "λαθάκι" είναι ότι ο γ.τ. είναι έλλειψη και όχι υπερβολή
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
ledzeppelinick
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Undead
Εκκολαπτόμενο μέλος


αν θεωρήσουμε
άρα
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


Η ελάχιστη απόσταση είναι mind=d(4)=SQRT(17)/2
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


απο το βιβλιο "ολοκληρωματα" του δ.νταβου αντιγραφω μια πολυ ωραια ασκηση.
εστω f παραγωγισιμη στο [α,α+3] για την οποια υποθετουμε οτι ισχυει.να δειξετε οτι υπαρχει
στο (α,α+3) ωστε η εφαπτομενη της στο
να ειναι παραλληλη στον αξονα x.
Στα παρακάτω με S(α,β)f(x)dx συμβολίζω το ορισμένο ολοκλήρωμα της f με κάτω όριο ολοκλήρωσης το α και πάνω το β. Όπου γράφω ΘΜΤΟΛ σημαίνει θεώρημα μέσης τιμής ολοκληρωτικού λογισμού. Αν είναι εκτός ύλης πρέπει να αποδειχτεί. Η απόδειξη είναι απλή και υπάρχει στο βιβλίο. Για λόγους πληρότητας την γράφω μετά τη λύση της άσκησης.
f παραγωγίσιμη [α,α+3] -> f συνεχής [α,α+3]
Από εκφώνηση έχουμε S(α,α+2)f(x)dx=S(α+1,α+3)f(x)dx ->
-> S(α,α+2)f(x)dx=S(α+1,α+2)f(x)dx+S(α+2,α+3)f(x)dx ->
-> S(α,α+2)f(x)dx=-S(α+2,α+1)f(x)dx+S(α+2,α+3)f(x)dx ->
-> S(α,α+2)f(x)dx+S(α+2,α+1)f(x)dx=S(α+2,α+3)f(x)dx ->
-> S(α,α+1)f(x)dx=S(α+2,α+3)f(x)dx
Θέτω S(α,α+1)f(x)dx=S(α+2,α+3)f(x)dx=I
f συνεχής στο [α,α+1] -> ΘΜΤΟΛ: υπάρχει ξ1 στο (α,α+1) ώστε f(ξ1)=S(α,α+1)f(x)=Ι
f συνεχής στο [α+2,α+3] -> ΘΜΤΟΛ :υπάρχει ξ2 στο (α+2,α+3) ώστε f(ξ2)=S(α+2,α+3)f(x)=Ι
Άρα f(ξ1)=f(ξ2)=I και προφανώς α<ξ1<α+1<α+2<ξ2<α+3
f συνεχής στο [ξ1,ξ2], f παραγωγίσιμη στο (ξ1,ξ2) και f(ξ1)=f(ξ2) ->
-> Θεώρημα Rolle : υπάρχει x0 στο (ξ1,ξ2) ώστε f΄(x0)=0
Εξίσωση εφαπτομένης στο Α(x0,f(x0))
y-f(x0)=f΄(x0)(x-x0) -> y=f΄(x0)x+f(x0)-x0f΄(x0) -> y=f(x0) παράλληλη στον άξονα x
ΑΠΟΔΕΙΞΗ ΘΕΩΡΗΜΑΤΟΣ ΜΕΣΗΣ ΤΙΜΗΣ ΟΛΟΚΛΗΡΩΤΙΚΟΥ ΛΟΓΙΣΜΟΥ
Θεώρημα: Αν μία συνάρτηση f είναι συνεχής στο διάστημα [α,β] (α<β) τότε υπάρχει τουλάχιστον ένα ξ στο διάστημα (α,β) τέτοιο ώστε f(ξ)=S(α,β)f(t)dt/(β-α)
Επειδή η f είναι συνεχής στο [α,β], τότε η F με τύπο F(x)=S(α,x)f(t)dt είναι παραγωγίσιμη και συνεπώς και συνεχής στο [α,β] με πρώτη παράγωγο F΄(x)=f(x) για κάθε x στο [α,β]
F(α)=S(α,α)f(t)dt=0
F(β)=S(α,β)f(t)dt
F συνεχής στο [α,β] και παραγωγίσιμη στο (α,β), οπότε σύμφωνα με το θεώρημα μέσης τιμής υπάρχει τουλάχιστον ένα ξ στο διάστημα (α,β) τέτοιο ώστε
F΄(ξ)=(F(β)-F(α))/(β-α) -> f(ξ)=S(α,β)f(t)dt/(β-α)
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


i) f΄(x)=ln[g(x)]+(e^x) για κάθε x ανήκει R
ii) S(α,x)f(t)dt>=f(x-α) για κάθε x ανήκει στο R
iii) f(β)=f΄(0) και f(0)=0
(α) να αποδείξετε ότι υπάρχει μοναδικό ξ στο R τέτοιο ώστε [g(ξ)]^2=e^(-2*(e^ξ)) για το οποίο ισχύει 0<g(ξ)<1
S(α,x)f(t)dt : ορισμένο ολοκλήρωμα της f με κάτω όριο ολοκλήρωσης το α και πάνω όριο το x
(β) να αποδείξετε ότι η f παρουσιάζει ολικό ελάχιστο στο σημείο (ξ, f(ξ)) το οποίο είναι και το μοναδικό ακρότατο της Cf.
(γ) να αποδείξετε ότι η Cg δεν μπορεί να έχει κατακόρυφες ασύμπτωτες
(δ) Αν η f είναι δύο φορές παραγωγίσιμη στο γ ανήκει R, η g είναι παραγωγίσιμη στο γ και ισχύει γ=lnf΄΄(γ) τότε η Cg έχει οριζόντια εφαπτομένη στο (γ, g(γ))
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
ledzeppelinick
Πολύ δραστήριο μέλος


β)για χ>=ξ, f'(x)>=f'(ξ) , f(χ)>=0 οπου ξ το ξ του προηγ ερωτηματος και f' γν αυξουσα. για χ=<ξ, f'(χ)=<f'(ξ), f'(χ)=<0. η f γν φθινουσα στο (-οο,0) και γν αυξουσα στο (0,+οο) άρα παρουσιαζει ολικο ελαχιστο στο ξ το f(ξ) το οποιο ειναι μοναδικο αφου η f ειναι ορισμενη στο R ειναι παραγωγισιμη και το μοναδικο σημειο οπου f'(χ)=0 είναι το (ξ,f(ξ))
γ) η g ειναι ορισμενη στο R οποτε δεν παρουσιαζει κατακορυφες ασυμπτωτες
δ)αρκει ν.δ.ο. g'(γ)=0. απο τη δοσμενη σχεση i) λύνουμε ως προς g g(x)=e^(f'(x)-e^x) και αφου η g παραγωγισιμη στο γ έχουμε g'(γ)=(f''(γ)-e^γ)*e^(f'(γ)-e^γ) άρα για να ισχυει g'(γ)=0 αρκει f''(γ)=e^γ, lnf''(γ)=γ το οποιο ισχυει
-----------------------------------------
με συγχωρειτε για τα λαθη και για τις ελλειψεις απλα εκανα μια προσπαθεια να την προσεγγισω! θα ηθελα να δω και την λυση mr. geoste για να διορθοθω!! αν δεν θελετε να την γραψετε εδω στειλτε την μου στο προφιλ μου! Ευχαριστω εκ των προτερων! :thanks:
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


Όσον αφορά την απάντησή σου στο γ) δεν είναι σωστή. Για παράδειγμα θεώρησε την συνάρτηση
f(x)=1/x, x διάφορο 0
f(x)=0 , x=0
Η f είναι ορισμένη στο R αλλά παρουσιάζει στο x0=0 κατακόρυφη ασύμπτωτη (άξονας y΄y)
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
ledzeppelinick
Πολύ δραστήριο μέλος



Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


Αν μία συνάρτηση είναι ΣΥΝΕΧΗΣ (όχι απλά ορισμένη) σε ένα σημείο x0 τότε ΔΕΝ έχει κατατκόρυφη ασύμπτωτη στο x0.
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
m3Lt3D
Πολύ δραστήριο μέλος


μια διαφορετικη αποδειξη:Μια απόδειξη για το :ανκαι
τότε
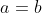
αν θεωρήσουμετότε
άρα
είναι γν. αύξουσα άρα και 1-1
άραdx=0 Leftrightarrow F(a)=F(b) Leftrightarrow a=b)
εστω α<β. αφου f(x)>0=>
ομοια για β<α.
αρα α=β
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
ledzeppelinick
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


ναι καταλαβα! ευχαριστω! :thanks:άρα λυνουμε την εξισωση στο α ερωτημα ως προς g και αποδεικνυουμε οτι δεν απεριζεται σε κανενα σημειο το οριο της? τι κανουμε? η λεμε οτι ειναι συνεχης επειδη ειναι ιση με ριζαe^(-2*(e^χ))?? ευχαριστω εκ των προτερων!!
Λύνουμε ως προς g και προκύπτει g(x)=e^(f΄(x)-(e^x)). Άρα g συνεχής στο R, αφού f΄ συνεχής στο R. Άρα δεν έχει κατακόρυφες ασύμπτωτες.
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
ledzeppelinick
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
ledzeppelinick
Πολύ δραστήριο μέλος


-----------------------------------------
οκ το αλλαξατε στα δεδομενα!! ευχαριστω!! και συγγνωμη για το πρηξιμο

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
odyracer18
Νεοφερμένο μέλος


Ξαναδές την λίγο γιατί είναι λάθος.Αυτό που λες δεν είναι σωστό δηλαδή,
f(z)=f(α+βi)=f(α)+f(βi)
αφού , απο υπόδεση ισχύει ότι f(z1+z2)=f(z1)+f(z2)
οπότε, για z1=α και z2=βi γίνεται
f(z)=f(α+βi)=f(α)+f(βi)
σορρυ,αλλά το είχα γράψει λίγο σύντομα και δεν τα αιτιολογούσα όλα
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Metal-Militiaman
Νεοφερμένο μέλος


(και 4ο δεν θα με χαλούσε,αν μου στέλνατε τις απαντήσεις)
https://www.ypepth.gr/themata/them_mat_kat_c_hmer_epan_0705.pdf
νομίζω ότι κάτι δεν μου καλλάει στο τρίτο ερώτημα του 3ου θέματος
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 0 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 289 μέλη διάβασαν αυτό το θέμα:
- Maynard
- foxypup
- Pars3c
- mikke
- thepigod762
- 98.8%chimpanzee
- trifasikodiavasma
- ggl
- ioanna2007
- Hased Babis
- Mariosm.
- infection54
- Jesse_
- topg
- eukleidhs1821
- bill09876
- Debugging_Demon
- mali
- Joji
- Ness
- Helen06
- Scandal
- synthnightingale
- arko
- BillyTheKid
- Magigi
- Paragontas7000
- Unboxholics
- just some guy
- george777
- Wonderkid
- IceCream05
- Abiogenesis
- GeorgePap2003
- katia.m
- giannhs2001
- paul
- Praxis
- Apocalypse
- shezza94
- desp1naa
- rempelos42
- Sherlockina
- oups
- Dimgeb
- spring day
- KingOfPop
- mpapa
- Chrisa
- Physicsstudent
- tsiobieman
- P.Dam.
- persi
- theodoraooo
- PanosBat
- kost28
- mikriarchitectonissa
- BILL KEXA
- Dr. Gl. Luminous
- Eleftheria2
- Lathy
- bruh_234
- Miranda32
- SlimShady
- kallikd
- nucomer
- alpha.kappa
- Eeeee
- J.Cameron
- Marple
- Kitana
- F1L1PAS
- sophiaa
- VFD59
- papa2g
- το κοριτσι του μαη
- srg96
- Hopeful22
- Φινεύς
- Phys39
- Anta2004
- fairyelly
- Pharmacist01
- jYanniss
- Panagiotis849
- Kokro
- augustine
- Nikoletaant
- Mashiro@Iberan
- margik
- Mammy Nun
- Pastramis
- Σωτηρία
- Appolon
- panosveki
- Nickt23
- igeorgeoikonomo
- Steliosgkougkou
- QWERTY23
- Ameliak
- aladdin
- nimbus
- Φωτεινη Τζα.
- marian
- Georgekk
- xrisamikol
- the purge
- Dora140303
- Machris
- s93060
- Nikitas18
- Stif6
- stav.mdp
- damn
- aekaras 21
- Anthropaki
- Angelos12345
- ioannam
- Μάρκος Βασίλης
- skyway
- Nick2325
- Nala
- Manolo165
- Ryuzaki
- T C
- Devilshjoker
- El_
- George9989
- TonyMontanaEse
- globglogabgalab
- constansn
- barkos
- katerinavld
- fenia
- An_uknown_world
- Jimmis18
- maria2001
- KingPoul
- Xara
- thecrazycretan
- abcdefg12345
- Κλημεντίνη
- ale
- panagiotis G
- mechaniceng
- Giii
- calliope
- Tequila
- natalix
- Cortes
- Alexecon1991
- pepsoula
- Mariaathens
- Lia 2006
- 1205
- παιδι για κλαματα
- Alexandros36k
- alexd99
- chembam
- Specon
- Dr House
- panagiotis23
- Johnman97
- rhymeasylum
- Αννα Τσιτα
- KaterinaL
- Libertus
- LeoDel
- iminspain
- den antexw allh apotyxia
- Λαμπρινηη
- Mendel2003
- Ijt
- drosos
- Κορώνα
- JohnGreek
- Αρχηγος_β3
- alexandra_
- ΘανάσοςG4
- Dimitris9
- Birtjan
- george7cr7
- NickT
- Bgpanos
- JKTHEMAN
- nicole1982
- χημεια4λαιφ
- Stroka
- Kostakis45
- charmander
- leo41
- EiriniS20
- Αριάνα123
- MarilynSt
- iManosX13
- Nefh_
- Viedo
- Βλα
- suaimhneas
- george pol
- kristinbacktoschool
- fearless
- Rene2004
- Steffie88
- Slytherin
- jimnikol21
- Unseen skygge
- cel123
- jul25
- Thanos_D
- Ireneeneri
- tasost
- Mukumbura
- xxxtolis
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki



