Συλλογή ασκήσεων και τεστ στα Μαθηματικά Προσανατολισμού

[rebel]

Καλησπέρα. Προσωπικά δεν έχω το βιβλίο. Το μόνο που έχω βρει στο διαδίκτυο είναι οι λύσεις επιλεγμένων ασκήσεων από τα "θέματα εξετάσεων" που είναι στο τέλος των κεφαλαίων. Αυτές βρίσκονται εδώ

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Μαριαντα]

Σας ευχαριστω πολυ!

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Civilara]

Θεωρούμε τις δύο φορές παραγωγίσιμες συναρτήσεις

,για τις οποίες ισχύουν

και

.Ν.Δ.Ο. για κάθε

υπάρχει

,ώστε

.

Ισχύει g(x) διάφορο 0 και g΄΄(x) διάφορο 0 στο (0,1)

Θεωρούμε την συνάρτηση h(x)=f΄(x)g(x)-f(x)g΄(x). Επειδή οι f και g έχουν συνεχή πρώτη παράγωγο στο [0,1] και είναι δύο φορές παραγωγίσιμες στο (0,1) τότε και η h είναι συνεχής στο [0,1] και παραγωγίσιμη στο (0,1) με πρώτη παράγωγο:

h΄(x)=f΄΄(x)g(x)-f(x)g΄΄(x), x ανήκει (0,1)

h(0)=f΄(0)g(0)-f(0)g΄(0)=f΄(0)*0-0*g΄(0)=0
h(1)=f΄(1)g(1)-f(1)g΄(1)=f΄(1)*0-0*g΄(1)=0
Επομένως h(0)=h(1)=0

Η h είναι συνεχής στο [0,1], παραγωγίσιμη στο (0,1) και ισχύει h(0)=h(1). Επομένως σύμφωνα με το θεώρημα Rolle υπάρχει τουλάχιστον ένα ξ στο (0,1) τέτοιο ώστε h΄(ξ)=0 <=> f΄΄(ξ)g(ξ)-f(ξ)g΄΄(ξ)=0 <=> f΄΄(ξ)/g΄΄(ξ)=f(ξ)/g(ξ) αφού g΄΄(ξ) διάφορο 0 και g(ξ) διάφορο 0.

Επομένως έχει αποδειχθεί το ζητούμενο για x=ξ.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[rebel]

Επομένως σύμφωνα με το θεώρημα Rolle υπάρχει τουλάχιστον ένα ξ στο (0,1) τέτοιο ώστε h΄(ξ)=0 <=> f΄΄(ξ)g(ξ)-f(ξ)g΄΄(ξ)=0 <=> f΄΄(ξ)/g΄΄(ξ)=f(ξ)/g(ξ) αφού g΄΄(ξ) διάφορο 0 και g(ξ) διάφορο 0.

Η άσκηση όμως δεν ζητάει αυτό. Απ' ότι κατάλαβα πρέπει να δείξουμε ότι αν σταθερό, τότε υπάρχει

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[C.J.S.]

Μια ασκηση που δεν μπορω να βγαλω!
Δινετε συναρτηση F συνεχης με F απο το R στο (-οο,1) με F(0)=F(1)=1/2
και g συνεχης απο το 1/2 στο απειρο με g(2)=3 και g(3)=1

1)NΔΟ υπαρχει τουλαχιστον ενα Χ που ανηκει στο (0,1) ωστε F(Χ)=2Χ
2)ΝΔΟ υπαρχει ενα τουλαχιστον Χ2 που ανηκει στο (2,3) ωστε g(Χ2)=Χ2
3)ΝΔΟ υπαρχει ξ ανηκει στο R ωστε να ισχυει F(ξ)*g(ξ)=ξ

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[rebel]

Tα δύο πρώτα ερωτήματα είναι προφανή. Το τελευταίο προκύπτει με Bolzano στο διάστημα .

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[C.J.S.]

Tα δύο πρώτα ερωτήματα είναι προφανή. Το τελευταίο προκύπτει με Bolzano στο διάστημα .

Ευχαριστώ πολύ!!Ακριβώς αυτό ήθελα το διάστημα που θα κάνω το τρίτο Bolzano!!

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[rebel]

Αν όπου παραγωγίσιμες στο , δείξτε ότι για κάθε

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Civilara]

Αν όπου παραγωγίσιμες στο , δείξτε ότι για κάθε

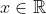
Μιας και δεν τη λύνει κανένας...

f(x)g(x)=e^x διάφορο 0 για κάθε x ανήκει R => f(x) διάφορο 0 και g(x) διάφορο 0 για κάθε x ανήκει R. Συγκεκριμένα f(x)g(x)=e^x>0 για κάθε x ανήκει R => f(x)>0 και g(x)>0 για κάθε x ανήκει R ή f(x)<0 και g(x)<0 για κάθε x ανήκει R.

Επειδή f(x) διάφορο 0 τότε g(x)=(e^x)/f(x) για κάθε x ανήκει R.
Η f είναι παραγωγίσιμη στο R οπότε και η g είναι παραγωγίσιμη στο R με πρώτη παράγωγο

g΄(x)=[(f(x)-f΄(x))/(f(x)^2)](e^x), x ανήκει R

Θεωρούμε την συνάρτηση h(x)=4f΄(x)g΄(x)-(e^x), x ανήκει R.

Έχουμε διαδοχικά

h(x)=4f΄(x)g΄(x)-(e^x)=4f΄(x)[(f(x)-f΄(x))/(f(x)^2)](e^x)-(e^x)=[((4f΄(x)(f(x)-f΄(x)))/(f(x)^2))-1](e^x)=
=[(-(f(x)^2)-4(f΄(x)^2)+4f΄(x)f(x))/(f(x)^2)](e^x)=-[((f(x)^2)+4(f΄(x)^2)-4f΄(x)f(x))/(f(x)^2)](e^x)=
=-[((f(x)-2f΄(x))^2)/(f(x)^2)](e^x)=-[(f(x)-2f΄(x))/f(x))^2](e^x)<=0 για κάθε x ανήκει R

h(x),=0 => 4f΄(x)g΄(x)-(e^x)<=0 => 4f΄(x)g΄(x)<=e^x για κάθε x ανήκει R

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Antpal]

Μια καλή άσκηση εύρεσης τύπου .

´Έστω f μια παραγωγίσιμη συνάρτηση για την οποία ισχύει :

(χ^χ)f´(χ)+(χ^χ)f(x)lnx =e^x , x>0

Άν f(1)=0 να βρεθεί ο τύπος της f.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Antpal]

Ακριβώς το ίδιο σκεφτόμουν και εγώ.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[φρι]

Μια καλή άσκηση εύρεσης τύπου .

´Έστω f μια παραγωγίσιμη συνάρτηση για την οποία ισχύει :

(χ^χ)f´(χ)+(χ^χ)f(x)lnx =e^x , x>0

Άν f(1)=0 να βρεθεί ο τύπος της f.

θα βρουμε το f'(1) που κανει e,και μετα θα παρουμε ορια?

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Antpal]

Πώς σκοπεύεις να δουλεψεις με όρια;

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Civilara]

Μια καλή άσκηση εύρεσης τύπου .

´Έστω f μια παραγωγίσιμη συνάρτηση για την οποία ισχύει :

(x^x)f´(x)+(x^x)f(x)lnx =e^x , x>0

Άν f(1)=0 να βρεθεί ο τύπος της f.

(x^x)f´(x)+(x^x)f(x)lnx =e^x <=> (x^x)(f΄(x)+f(x)lnx)=e^x, x>0

Θεωρούμε την συνάρτηση G(x)=x^x=e^(ln(x^x))=e^(xlnx), x>0. Η συνάρτηση G είναι συνεχής και παραγωγίσιμη στο (0,+οο) με πρώτη παράγωγο:

G΄(x)=(e^(xlnx))΄=(e^(xlnx))(xlnx)΄=(x^x)((x)΄lnx+x(lnx)΄)=(x^x)(1*lnx+x*(1/x)) => G΄(x)=(x^x)(lnx+1), x>0

Θεωρούμε την συνάρτηση F(x)=f(x)(e^(-x)), x>0. Επειδή η f είναι παραγωγίσιμη στο (0,+οο) τότε και η F είναι παραγωγίσιμη στο (0,+οο) (άρα και συνεχής στο (0,+οο)) με πρώτη παράγωγο:

F΄(x)=(f(x)(e^(-x))΄=f΄(x)(e^(-x))+f(x)(e^(-x))΄=f(x)(e^(-x))-f(x)(e^(-x)) => F΄(x)=(f΄(x)-f(x))(e^(-x)), x>0

Θεωρούμε την συνάρτηση H(x)=(x^x)f(x)(e^(-x))=G(x)F(x), x>0

Επειδή οι G και F είναι παραγωγίσιμες στο (0,+οο) τότε και η H είναι παραγωγίσιμη στο (0,+οο), οπότε είναι και συνεχής στο (0,+οο), με πρώτη παράγωγο:

H΄(x)=G΄(x)F(x)+G(x)F΄(x)=(x^x)(lnx+1)f(x)(e^(-x))+(x^x)(f΄(x)-f(x))(e^(-x))
H΄(x)=(x^x)(e^(-x))[f(x)(lnx+1)+f΄(x)-f(x)]=(x^x)(e^(-x))[f΄(x)+f(x)lnx],x>0

Επειδή (x^x)(f΄(x)+f(x)lnx)=e^x για κάθε x>0 τότε έχουμε:

H΄(x)=(x^x)(e^(-x))[f΄(x)+f(x)lnx]={(x^x)[f΄(x)+f(x)lnx]}(e^(-x))=(e^x)(e^(-x))=e^0=1, x>0

Θεωρούμε την συνάρτηση h(x)=x. Η συνάρτηση h είναι συνεχής και παραγωγίσιμη στο R με πρώτη παράγωγο h΄(x)=1.

Οι συναρτήσεις H και h είναι συνεχείς και παραγωγίσιμες στο (0,+οο) και για κάθε x στο (0,+οο) ισχύει

H΄(x)=h΄(x)

Επομένως υπάρχει πραγματική σταθερά c τέτοια ώστε H(x)=h(x)+c για κάθε x ανήκει (0,+οο). Έχουμε

H(x)=h(x)+c <=> (x^x)f(x)(e^(-x))=x+c <=> ((x/e)^x)f(x)=x+c <=> f(x)=((e/x)^x)(x+c), x>0

Έχουμε f(1)= e(1+c). Επειδή f(1)=0 τότε 1+c=0 => c=-1. Επομένως

f(x)=((e/x)^x)(x-1), x>0

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Antpal]

Πολύ ωραία και δημιουργική η λύση σου.Να και μια πιο σύντομη.

Η δοσμένη σχέση γίνεται :

f´(x)+lnxf(x)=e^x/x^x. (1)

Εστω g(x)=lnx. Τότε. g(x)=lnx+(x/x)-(x/x)=(x)´lnx+x(lnx)´-1
( G(x))´=(xlnx-x)´

Πολ/ζω την (1) με e^(xlnx-x). Αρα γίνεται e^(xlnx-x)f´(x)+[e^(xlnx-x)](xlnx-x)´f(x)=(e^x/x^x)(e^(xlnx-x))=1
[e^(xlnx-x)f(x)]´=(x)´
e^(xlnx-x)f(x)=x+c , f(1)=0 άρα c=-1

Συνεπώς. e^(xlnx-x)f(x)=x-1, f(x)=[(x-1)e^x]/x^x

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[rebel]

Για την παραγωγίσιμη συνάρτηση ισχύει

για κάθε , όπου με σταθεροί αριθμοί. Να αποδείξετε ότι η είναι σταθερή στο

Από εδώ

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Civilara]

Για την παραγωγίσιμη συνάρτηση ισχύει

για κάθε , όπου με σταθεροί αριθμοί. Να αποδείξετε ότι η είναι σταθερή στο

Από εδώ

a<b<c => b-a>0, c-b>0

(f(b)-f(a))/(b-a)<=3f΄(x)<=2((f(c)-f(b))/(c-b)) <=> (1/3)((f(b)-f(a))/(b-a))<=f΄(x)<=(2/3)((f(c)-f(b))/(c-b)), x ανήκει R

Η συνάρτηση f είναι παραγωγίσιμη στο R οπότε είναι και συνεχής στο R.

Θεωρούμε x,y ανήκουν R με x<y. Η συνάρτηση f είναι συνεχής στο [x,y] και παραγωγίσιμη στο (x,y). Επομένως σύμφωνα με το Θεώρημα Μέσης Τιμής υπάρχει τουλάχιστον ένα ξ1 ανήκει (x,y) τέτοιο ώστε:

f΄(ξ1)=(f(y)-f(x))/(y-x)

Θεωρούμε x,y ανήκουν R με y<x. Η συνάρτηση f είναι συνεχής στο [y<x] και παραγωγίσιμη στο (y,x). Επομένως σύμφωνα με το Θεώρημα Μέσης Τιμής υπάρχει τουλάχιστον ένα ξ2 ανήκει (y,x) τέτοιο ώστε:

f΄(ξ2)=(f(x)-f(y))/(x-y)=(f(y)-f(x))/(y-x)

Επομένως για κάθε x,y ανήκουν R με x διάφορο y υπάρχει τουλάχιστον ένα ξ ανήκει R τέτοιο ώστε

f΄(ξ)=(f(y)-f(x))/(y-x)

Επομένως έχουμε:

(1/3)((f(b)-f(a))/(b-a))<=f΄(ξ)<=(2/3)((f(c)-f(b))/(c-b))
(1/3)((f(b)-f(a))/(b-a))<=(f(y)-f(x))/(y-x)<=(2/3)((f(c)-f(b))/(c-b)), x,y ανήκουν R με x διάφορο y

Για y=b και x=a έχουμε:

(1/3)((f(b)-f(a))/(b-a))<=(f(b)-f(a))/(b-a)<=(2/3)((f(c)-f(b))/(c-b))

Χρησιμοποιούμε την πρώτη ανισότητα της διπλής ανισότητας:

(1/3)((f(b)-f(a))/(b-a))<=(f(b)-f(a))/(b-a) <=> (f(b)-f(a))<=3(f(b)-f(a)) <=> 2(f(b)-f(a))>=0 <=> f(b)-f(a)>=0 <=> f(a)<=f(b)

Άρα

f(a)<=f(b) <=> f(b)-f(a)>=0 <=> (f(b)-f(a))/(b-a)>=0 <=> (1/3)((f(b)-f(a))/(b-a))>=0


Για y=c και x=b έχουμε:

(1/3)((f(b)-f(a))/(b-a))<=(f(c)-f(b))/(c-b)<=(2/3)((f(c)-f(b))/(c-b))

Χρησιμοποιούμε την δεύτερη ανισότητα της διπλής ανισότητας:

(f(c)-f(b))/(c-b)<=(2/3)((f(c)-f(b))/(c-b)) <=> 3(f(c)-f(b))<=2(f(c)-f(b)) <=> f(c)-f(b)<=0 <=> f(c)<=f(b)

Άρα

f(c)<=f(b) <=> f(c)-f(b)<=0 <=> (f(c)-f(b))/(c-b)<=0 <=> (2/3)((f(c)-f(b))/(c-b))<=0

Έχει βρεθεί ότι (2/3)((f(c)-f(b))/(c-b))<=0<=(1/3)((f(b)-f(a))/(b-a))

Επίσης από την ανίσωση (1/3)((f(b)-f(a))/(b-a))<=f΄(x)<=(2/3)((f(c)-f(b))/(c-b)) η οποία ισχύει για κάθε x ανήκει R προκύπτει ότι

(1/3)((f(b)-f(a))/(b-a))<=(2/3)((f(c)-f(b))/(c-b))

Από τις ανισότητες (2/3)((f(c)-f(b))/(c-b))<=0<=(1/3)((f(b)-f(a))/(b-a)) και (1/3)((f(b)-f(a))/(b-a))<=(2/3)((f(c)-f(b))/(c-b)) προκύπτει ότι

(2/3)((f(c)-f(b))/(c-b))=(1/3)((f(b)-f(a))/(b-a))=0 => f(a)=f(b)=f(c)=0

Αντικαθιστώντας τα f(a)=f(b)=f(c)=0 στην αρχική ανισότητα προκύπτει:

0<=f΄(x)<=0 => f΄(x)=0 για κάθε x ανήκει R

Άρα υπάρχει σταθερά c ώστε f(x)=c για κάθε x ανήκει R που σημαίνει ότι η f είναι σταθερή συνάρτηση.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[rebel]

Λίγο διαφορετικά, από ΘΜΤ


οπότε η αρχική ανισότητα γίνεται



Για από την αριστερή ανισότητα παίρνουμε
Για από την δεξιά ανισότητα παίρνουμε

Από (1),(2),(3) παίρνουμε και το ζητούμενο αποδείχθηκε.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[rebel]

Έστω τρεις φορές παραγωγίσιμες με . Δείξτε ότι υπάρχει με

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Civilara]

Έστω τρεις φορές παραγωγίσιμες με . Δείξτε ότι υπάρχει με

Θεωρούμε την συνάρτηση h(x)=f(x)-g(x), x ανήκει R. Επειδή οι f και g είναι 3 φορές παραγωγίσιμες στο R τότε και η h είναι 3 φορές παραγωγίσιμη στο R και ισχύει:

h΄(x)=f΄(x)-g΄(x)
h΄΄(x)=f΄΄(x)-g΄΄(x)
h΄΄΄(x)=f΄΄΄(x)-g΄΄΄(x)

για κάθε x ανήκει R

Η αρχική ανίσωση γράφεται ισοδύναμα:

3f(x)-2f(1)-f(2)>=3g(x)-2g(1)-g(2) <=> 3f(x)-3g(x)>=2f(1)-2g(1)+f(2)-g(2) <=>
<=> 3(f(x)-g(x))>=2(f(1)-g(1))+(f(2)-g(2)) <=> 3h(x)>=2h(1)+h(2) <=> h(x)>=(2/3)h(1)+(1/3)h(2) για κάθε x ανήκει R

Για x=1 έχουμε:
3h(1)>=2h(1)+h(2) <=> h(1)>=h(2)

Για x=2 έχουμε:
3h(2)>=2h(1)+h(2) <=> 2h(2)>=2h(1) <=> h(2)>=h(1)

Από τις δύο τελευταίες σχέσει προκύπτει ότι h(1)=h(2)=c όπου c ανήκει R

Η h είναι παραγωγίσιμη στο R άρα και συνεχής στο R. Η h είναι συνεχής στο [1,2], οπότε σύμφωνα με το θεώρημα μέγιστης & ελάχιστης τιμής συνεχών συναρτήσεων, υπάρχουν α,β στο [1,2] τέτοια ώστε αν m=h(α) και M=h(β) με m<=M να ισχύει m<=h(x)<=M για κάθε x στο [1,2].

Για x=1 έχουμε
m<=h(1)<=M <=> (1/3)m<=(1/3)h(1)<=(1/3)M

Για x=2 έχουμε
m<=h(2)<=M <=> (2/3)m<=(2/3)h(2)<=(2/3)M

Προσθέτοντας κατά μέλη τις 2 τελευταίες ανισότητες προκύπτει ότι:
m<=(1/3)h(1)+(2/3)h(2)<=M

Επομένως σύμφωνα με το θεώρημα ενδιαμέσων τιμών υπάρχει τουλάχιστον ένα x0 στο (1,2) τέτοιο ώστε h(x0)=(1/3)h(1)+(2/3)h(2)
Έχουμε h(x0)=(1/3)h(1)+(2/3)h(2)=(1/3)c+(2/3)c=c όπου m<=c<=M.

Άρα h(1)=h(x0)=h(2)=c

Η ανισότητα h(x)>=(2/3)h(1)+(1/3)h(2) γράφεται ισοδύναμα h(x)>=c εφόσον h(1)=h(2)=c

Ισχύει h(x)>=h(1) για κάθε x ανήκει R που σημαίνει ότι η h παρουσιάζει ολικό ελάχιστο οποτε και τοπικό ελάχιστο στο x1=1. Επειδή η h είναι ορισμένη στο R, παραγωγίσιμη στο x1=1 και παρουσιάζει τοπικό ελάχιστο στο x1=1 τότε σύμφωνα με το θεώρημα Fermat ισχύει h΄(1)=0.

Ισχύει h(x)>=h(2) για κάθε x ανήκει R που σημαίνει ότι η h παρουσιάζει ολικό ελάχιστο οποτε και τοπικό ελάχιστο στο x2=2. Επειδή η h είναι ορισμένη στο R, παραγωγίσιμη στο x2=2 και παρουσιάζει τοπικό ελάχιστο στο x2=2 τότε σύμφωνα με το θεώρημα Fermat ισχύει h΄(2)=0.

Ισχύει h(x)>=h(x0) για κάθε x ανήκει R που σημαίνει ότι η h παρουσιάζει ολικό ελάχιστο οποτε και τοπικό ελάχιστο στο x0. Επειδή η h είναι ορισμένη στο R, παραγωγίσιμη στο x0 και παρουσιάζει τοπικό ελάχιστο στο x0 τότε σύμφωνα με το θεώρημα Fermat ισχύει h΄(x0)=0.

Άρα h΄(1)=h΄(x0)=h΄(2)

Η h είναι δύο φορές παραγωγίσιμη στο [1,2] οπότε η πρώτη παράγωγος h΄ είναι παραγωγίσιμη στο (1,2) και συνεχής στο [1,2].

H h΄ είναι συνεχής στο [1,x0], παραγωγίσιμη στο (1,x0) και ισχύει h΄(1)=h΄(x0). Επομένως σύμφωνα με το θεώρημα Rolle υπάρχει τουλάχιστον ένα ξ1 στο (1,x0) τέτοιο ώστε h΄΄(ξ1)=0.

H h΄ είναι συνεχής στο [x0,2], παραγωγίσιμη στο (x0,2) και ισχύει h΄(x0)=h΄(2). Επομένως σύμφωνα με το θεώρημα Rolle υπάρχει τουλάχιστον ένα ξ2 στο (x0,2) τέτοιο ώστε h΄΄(ξ2)=0.

Άρα h΄΄(ξ1)=h΄΄(ξ2)=0

Η h είναι τρεις φορές παραγωγίσιμη στο [1,2] οπότε η δεύτερη παράγωγος h΄΄ είναι παραγωγίσιμη στο (1,2) και συνεχής στο [1,2].

H h΄΄ είναι συνεχής στο [ξ1,ξ2], παραγωγίσιμη στο (ξ1,ξ2) και ισχύει h΄΄(ξ1)=h΄΄(ξ2). Επομένως σύμφωνα με το θεώρημα Rolle υπάρχει τουλάχιστον ένα ξ στο (ξ1,ξ2) τέτοιο ώστε h΄΄΄(ξ)=0.

h΄΄΄(ξ)=0 <=> f΄΄΄(ξ)-g΄΄΄(ξ)=0 <=> f΄΄΄(ξ)=g΄΄΄(ξ)

Άρα υπάρχει τουλάχιστον ένα ξ ανήκει R τέτοιο ώστε f΄΄΄(ξ)=g΄΄΄(ξ)

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.