Ελληνική Μαθηματική Εταιρεία: Γενικό Θέμα

raf616 · 04-09-13

Αρχική Δημοσίευση από unπαικτable:
$\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\geq \frac{1}{671}=\frac{3}{2013} \Rightarrow$
$\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\leq \frac{3}{x+y+z} \Rightarrow$
$(x+y+z)\frac{1}{x}+(x+y+z)\frac{1}{y}+(x+y+z)\frac{1}{z}\geq 3 \Rightarrow$
$1+\frac{y}{x}+\frac{z}{x}+\frac{x}{y}+1+\frac{z}{y}+\frac{x}{z}+\frac{y}{z}+1\geq 3 \Rightarrow$
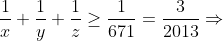
$\frac{y}{x}+\frac{z}{x}+\frac{x}{y}+\frac{z}{y}+\frac{x}{z}+\frac{y}{z}\geq 0$ ,που ισχυει αφου $x,y,z\succ 0$

α,β,γ,x,y πραγματικοι αριθμοι τετοιοι ωστε
${a}^{3}+ax+y=0$ , ${b}^{3}+bx+y=0$ , ${c}^{3}+cx+y=0$ με α $\neq$ β , β $\neq$ γ , α $\neq$ γ
Νδο α+β+γ=0 (Βαλκανιαδα Νεων 1999)

Έστω ${a}^{3}+ax+y=0 : (1)$ , ${b}^{3}+bx+y=0 : (2)$ και ${c}^{3}+cx+y=0 : (3)$ .

Παίρνουμε την $(1)$ και $(2)$ και έχουμε:

$\displaystyle{{a}^{3}+ax+y = {b}^{3}+bx+y \Leftrightarrow a^2 - b^3 + ax - bx = 0 \Leftrightarrow (a - b)(a^2 + ab + b^2) + x(a - b) = 0 \Leftrightarrow (a - b)(a^2 + ab + b^2 + x) = 0}$

Από την τελευταία παίρνουμε ότι $a^2 + ab + b^2 + x = 0 : (4)$ ,

αφού $a - b \neq 0$

Ομοίως από την $(1)$ και την $(3)$ παίρνουμε:

$a^2 + ac + c^2 + x = 0 : (5)$

Τώρα από τις $(4)$ και $(5)$ έχουμε:

$\displaystyle{a^2 + ab + b^2 + x = a^2 + ac + c^2 + x \Leftrightarrow b^2 - c^2 + ab - ac = 0 \Leftrightarrow (b - c)(b + c) + a(b - c) = 0 \Leftrightarrow (b - c)(a + b + c) = 0}$

Από την τελευταία παίρνουμε ότι $a + b + c = 0$ αφού $b - c \neq 0$

nikoslarissa · 04-09-13

Αρχική Δημοσίευση από Alejandro che 7:
αφου είναι μεγαλύτερο του 3/671 δεν θα ειναι και του 1/671; Μια απλή εφαρμογή της "Andreescu"(επίσημα BCS για τις συγκεκριμένες τριάδες) είναι η άσκηση προσωπικά θεωρώ ότι δεν θα έπεφτε σε κανέναν διαγωνισμό γιατί είναι πολύ εξειδικευμένη για Θαλή Ευκλείδη που συνήθως είναι επαρκείς οι σχολικές γνώσεις και πολύ απλή για Αρχιμήδη.

Ναι αλλά δεν μπορεί να ισχύει η ισότητα.Όχι οτι είναι λάθος έτσι απλά θα ήταν καλύτερο να είχε 3 αντί για 1 για να βγαίνει κατ ευθειαν από Andreescu.Συνήθως στις ανισοισότητες ζητάνε και πότε ισχύει η ισότητα.

raf616 · 04-09-13

Συγγνώμη, δικό μου λάθος... $\frac{3}{671}$ είναι το σωστό...

nikoslarissa · 04-09-13

Αν α,β,γ>0 νδο

raf616 · 04-09-13

Αρχική Δημοσίευση από nikoslarissa:
Αν α,β,γ>0 νδο

Από ΑΜ - ΓΜ έχω:

$a + 1 + \frac{1}{a} \geq 3\sqrt[3]{a \cdot 1 \cdot \frac{1}{a}} = 3$

Ομοίως:

$b + 1 + \frac{1}{b} \geq 3$

$c + 1 + \frac{1}{c} \geq 3$

Πολλαπλασιάζοντας κατά μέλη παίρνουμε τη ζητούμενη.

Alejandro che 7 · 04-09-13

Αρχική Δημοσίευση από nikoslarissa:
Αν α,β,γ>0 νδο

Αλλιώς $a+\frac{1}{a}\geq 2<br /> b+\frac{1}{b}\geq 2<br /> c+\frac{1}{c}\geq 2$

αφού α,β,γ>0 και η συνέχεια προφανής

nikosxdxd · 04-09-13

Αρχική Δημοσίευση από unπαικτable:
Πραγματικα δεν ειναι τοσο δυσκολη οσο ισςως να φαινεται... Ουτε ιδιαιτερα τεχνασματα χρειαζεται ουτε καποιες ιδιαιτερες γωνσεις.

Aυτο εννοω κι εγω... θυμαμαι οταν ασχολουμουν εντατικα στα 14-15 μου με μαθηματικη εταιρεια τα θεματα ηταν πολυ συνδυαστικα οχι αντικαταστασεις...

raf616 · 04-09-13

Εντάξει, μιλάμε για Θαλή και εισαγωγικά κυρίως θέματα...

raf616 · 05-09-13

Ας βάλω μία άσκση:

Να βρεθούν οι ακέραιες λύσεις της εξίσωσης:

$2x + 3y = 1993 - xy$

physicscrazy · 06-09-13

Αρχική Δημοσίευση από raf616:
Να βρεθούν οι ακέραιες λύσεις της εξίσωσης:

$2x + 3y = 1993 - xy$

2χ+3y=1993-χy<=>2χ+3y+χy+6=1993+6<=>(3+χ)(2+y)=1999

το 1999 ειναι πρωτος αρα οι παραγοντες θα ειναι 1 και 1999
1999 και 1
-1 και -1999
-1999 και -1

αρα 3+χ=1 και 2+y =1999<=>x=-2 και y=1997
3+x=1999 και 2+y=1<=>x=1996 και y=-1
3+x=-1 και 2+y=-1999<=>x=-4 και y=-2001
3+x=-1999 και 2+y=-1<=>x=-2002 και y=-3

nikoslarissa · 06-09-13

Μια ανισότητα δικής μου κατασκευής.Οποιος ήταν πριν από λίγο στο mathematica θα την είδε.
Για τους $x,y,z>0$ να δείξετε ότι

$2{x}^{6}+2{y}^{6}+2{z}^{6}+3\geq 3({x}^{2}yz+{y}^{2}xz+{z}^{2}xy)$

raf616 · 06-09-13

Tην είδα...

Αρχική Δημοσίευση από physicscrazy:
2χ+3y=1993-χy<=>2χ+3y+χy+6=1993+6<=>(3+χ)(2+y)=1999

το 1999 ειναι πρωτος αρα οι παραγοντες θα ειναι 1 και 1999
1999 και 1
-1 και -1999
-1999 και -1

αρα 3+χ=1 και 2+y =1999<=>x=-2 και y=1997
3+x=1999 και 2+y=1<=>x=1996 και y=-1
3+x=-1 και 2+y=-1999<=>x=-4 και y=-2001
3+x=-1999 και 2+y=-1<=>x=-2002 και y=-3

Σωστός.

POSITIVE · 08-09-13

Να βρεθεί ο μεγαλύτερος απ'τους $A=500^{999}$ , $B=999!$

Jonas · 14-09-13

Αρχίζουν τα μαθήματα στα κεντρικά της ΕΜΕ, στην Αθήνα. Καλή παρακολούθηση.

SonnY · 18-09-13

Παίδες ξέρουμε πότε είναι η 1η φάση φέτος??

POSITIVE · 20-09-13

Νομίζω 19 Οκτωβρίου.

SonnY · 22-09-13

positive απο που το μαθες αυτο?

POSITIVE · 22-09-13

Βασικά το υπέθεσα απ'το γεγονός ότι στις 19 (σύμφωνα με αυτό που ανέβασε ο Jonas) δεν θα γίνει μάθημα προετοιμασίας, αλλά πιθανόν να κάνω λάθος γιατί ούτε στις 9 και 16 Νοεμβρίου θα γίνει.

Jonas · 25-09-13

Η ΕΜΕ έβγαλε την ανακοίνωση με τις ημερομηνίες των φετινών διαγωνισμών.
Εγώ, λόγω Πανελλαδικών, φέτος δεν. ΚΑΛΗ ΕΠΙΤΥΧΙΑ σε όσους θα δώσουν.

raf616 · 25-09-13

Καλή επιτυχία σε όλους...

Ελληνική Μαθηματική Εταιρεία: Γενικό Θέμα

Νεοφερμένος

Δραστήριο μέλος

Νεοφερμένος

Δραστήριο μέλος

Νεοφερμένος

Πολύ δραστήριο μέλος

Διάσημο μέλος

Νεοφερμένος

Νεοφερμένος

Δραστήριο μέλος

Δραστήριο μέλος

Νεοφερμένος

Νεοφερμένος

Εκκολαπτόμενο μέλος

Εκκολαπτόμενο μέλος

Νεοφερμένος

Εκκολαπτόμενο μέλος

Νεοφερμένος

Εκκολαπτόμενο μέλος

Νεοφερμένος