Βοήθεια/Aπορίες στα Μαθηματικά Προσανατολισμού

Lost in the Fog · 18-02-14

να ρωτησω κατι ασχετο: γιατι καποιες ασκησεις που ειναι γραμμενες σε λατεξ δεν μπορω να τις δω?

rebel · 20-02-14

Αρχική Δημοσίευση από Lost in the Fog:
μια βοηθεια στις παρακατω ασκησεις...

Για την τρίτη το Α ερώτημα.
α)
Δίνεται ότι
$f( \eta \mu x ) = \sigma \upsilon \nu^2 x +x-1,\,\,(1)$
Παραγωγίζουμε και βγαίνει
$f'( \eta \mu x ) \sigma \upsilon \nu x =-2 \sigma \upsilon \nu x \eta \mu x +1,\,\,(2)$
Από την (1) και την (2) για $x=0$ βρίσκουμε $f(0)=0, f'(0)=1$ άρα πράγματι η $\left(\varepsilon\right)$ είναι η εφαπτομένη στο $(0,0)$
β)
Για να εφάπτεται η $\left(\varepsilon\right)$ στην γραφική παράσταση στο σημείο $M\left(x_0,h(x_0)\right)$ πρέπει και αρκεί το σύστημα
$(\Sigma):\begin{cases} M \in \left(\varepsilon\right) \\ h'\left(x_0\right)=\lambda_\varepsilon \end{cases}$
να έχει λύση. Το $(\Sigma)$ γράφεται:
$(\Sigma):\begin{cases} h(x_0)=x_0 \\ h'(x_0)=1\end{cases}$
και λύνοντάς το ( αποφεύγω τις λεπτομέρειες ) βρίσκουμε $x_0=0,\,\,a=1$ .
γ)
Μια που η $f'$ είναι συνεχής κάνουμε Bolzano για την $g(x)=f'(x)-x$ στο $\left[0, \frac{\sqrt{2}}{2}\right]$ . Για να βρούμε τo $f'\left(\frac{\sqrt{2}}{2}\right)$ βάζουμε στην (2) $x=\frac{\pi}{4}$
δ)
$\frac{f'(x)f(x)- \eta \mu 3 x }{\sqrt{x+1}-1}=\frac{\left(f'(x)f(x)- \eta \mu (3 x) \right)\left( \sqrt{x+1}+1 \right)}{\left( \sqrt{x+1}-1 \right)\left( \sqrt{x+1}+1 \right)}=\frac{\left(f'(x)f(x)- \eta \mu 3 x \right)\left( \sqrt{x+1}+1 \right)}{x}=\left( \frac{f(x)}{x} f'(x)-3 \frac{\eta \mu (3x)}{3x}\right)\left( \sqrt{x+1}+1 \right)$
oπότε
$\lim_{x \to 0} \frac{f'(x)f(x)- \eta \mu 3 x }{\sqrt{x+1}-1}=-4$
αφού
$\bigstar \lim_{x \to 0}\frac{f(x)}{x}=f'(0)=1 \bigstar \lim_{x \to 0} f'(x) = f'(0)=1 \bigstar \lim_{x \to 0} \frac{\eta \mu (3x)}{3x} = 1$

Mariaal · 20 Φεβρουαρίου 2014

Πώς αποδεικνυουμε οτι η συναρτηςη f(x) = (1+e^(2x))x+x^2+1 δε δεχεται ασύμπτωτες. Επιπλέον πως αποδεικνύω ότι η f(x)=0 ειπναι αδύνατη;

Civilara · 20-02-14

Αρχική Δημοσίευση από Mariaal:
Πώς αποδεικνυουμε οτι μια συναρτηση με πολυώνυμου 2ου βαθμου δε δεχεται ασύμπτωτες;

Μια πολυωνυμική συνάρτηση f(x)=αn*(x^n)+αn-1*(x^(n-1))+...+α1x+α0, αn διάφορο 0, οποιουδήποτε βαθμού n, n ανήκει N με n>=2 δεν έχει ασύμπτωτες. (Το ίδιο ισχύει και για την γραμμική συνάρτηση f(x)=α1*x+α0 και την σταθρή συνάρτηση f(x)=α0)

Επειδή η f είναι συνεχής στο R τότε η Cf δεν έχει κατακόρυφες ασύμπτωτες.

Αν αn>0 τότε lim(x->-oo)f(x)=-oo και lim(x->+oo)f(x)=+oo.
Αν αn<0 τότε lim(x->-oo)f(x)=+oo και lim(x->+oo)f(x)=-oo.
Άρα η Cf δεν έχει οριζόντιες ασύμπτωτες.

Αν αn>0 τότε lim(x->-oo)[f(x)/x]=+oo, lim(x->-oo)f(x)=-oo και lim(x->+oo)[f(x)/x]=0, lim(x->+oo)f(x)=+oo
Αν αn<0 τότε lim(x->-oo)[f(x)/x]=+oo, lim(x->-oo)f(x)=+oo και lim(x->+oo)[f(x)/x]=0, lim(x->+oo)f(x)=-oo
Άρα η Cf δεν έχει πλάγιες ασύμπτωτες.

lowbaper92 · 21-02-14

Αρχική Δημοσίευση από Mariaal:
Πώς αποδεικνυουμε οτι η συναρτηςη f(x) = (1+e^(2x))x+x^2+1 δε δεχεται ασύμπτωτες. Επιπλέον πως αποδεικνύω ότι η f(x)=0 ειπναι αδύνατη;

Επειδή το λάτεξ τα 'χει παίξει...

Dream Theater · 21-02-14

Θελω τη βοηθεια σας στον υπολογισμο του εξης ολοκληρωματος:

$\int_{4}^{9}(\sqrt{x})/(x+1)dx$

εφαρμοζω αντικατασταση και δε μπορω να το βγαλω με τιποτα!

rebel · 21 Φεβρουαρίου 2014

Γραψε λάθος.

DumeNuke · 21-02-14

Αρχική Δημοσίευση από styt_geia:
Με την αντικατάσταση $x=u^2,\,\,dx=2udu$ γίνεται
$\int_2^3 \frac{u}{u^2+1}du= \frac{1}{2}\int_2^3 \frac{2u}{u^2+1}du=\frac{1}{2}\int_2^3 \frac{\left(u^2+1\right)'}{u^2+1}du$
κλπ

Με αλλαγή των άκρων, μετά την αντικατάσταση: $2\rightarrow \sqrt{2}$ και $3\rightarrow \sqrt{3}$

rebel · 21-02-14

Με την αντικατάσταση $x=u^2,\,\,dx=2udu$ γίνεται
$\int_2^3 \frac{2u^2}{u^2+1}du=\int_2^3 \frac{2u^2+2-2}{u^2+1}du=\int_2^3 2 - \frac{2}{u^2+1}du$

Για το ολοκλήρωμα $\int_{2}^3 \frac{2}{u^2+1}du$ κάνουμε αντικατάσταση $u=\epsilon \phi t ,\,\,du=\frac{1}{\sigma \upsilon \nu ^2 t}dt$ και έχουμε

$\int_{2}^3 \frac{2}{u^2+1}du= \int_{\epsilon \phi ^{-1}(2)}^{\epsilon \phi ^{-1}(3)}\frac{2}{ \epsilon \phi^2 t+1}\frac{1}{\sigma \upsilon \nu ^2 t}dt= \int_{\epsilon \phi ^{-1}(2)}^{\epsilon \phi ^{-1}(3)} 2 dt= 2\left(\epsilon \phi ^{-1}(3)-\epsilon \phi ^{-1}(2)\right)$

Το αρχικό ολοκλήρωμα τελικά είναι $2(3-2)-2\left(\epsilon \phi ^{-1}(3)-\epsilon \phi ^{-1}(2)\right)$ και ελπίζω αυτή τη φορά να μην τα θαλάσσωσα.

Mariaal · 24 Φεβρουαρίου 2014

Ευχαριστώ!

aris-bas · 25-02-14

Θα ήθελα τη βοήθεια σας στις παρακάτω..
1)Έστω μια συνάρτηση f παραγωγισιμη στο (0,+00) με f(1)=e και

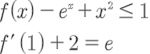
Να αποδειχθεί ότι f ' (1)+2=e

2)

i)Nα βρεθούν οι τιμές του α για τις οποίες η f δεν παρουσιαζει ακροτατα
ii)Για α=2 να βρεθεί το πλήθος των ριζών της f(x)=0

rebel · 25 Φεβρουαρίου 2014

1) Εφαρμογή του θεωρήματος Fermat για την $g(x)=f(x)-e^x+x^2$

2)
i) Είναι $f'(x)=3x^2+2(a-1)x+3$ με διακρίνουσα $\Delta = 4 (a-1)^2-4 \cdot 9$ οπότε η πρόταση «η f δεν έχει ακρότατα» είναι ισοδύναμη με τις προτάσεις
$\Delta \leq 0 \Leftrightarrow (a-1)^2 \leq 9 \Leftrightarrow |a-1| \leq 3 \Leftrightarrow -3 \leq a-1 \leq 3 \Leftrightarrow -2 \leq a \leq 4$
ii)
Έυκολα βρίσκουμε ότι $f(-1)f(-2)<0$ οπότε η f έχει τουλάχιστον μία ρίζα στο διάστημα $(-2,-1)$ . Η f επιπλέον είναι γνησίως αύξουσα για $a=2 \in [-2,4]$ οπότε η προηγούμενη ρίζα είναι και μοναδική.

Victoria Hislop · 25-02-14

Έχω ένα μεγάλο πρόβλημα. Οι εξετάσεις πλησιάζουν και εγώ δεν μπορω ακομα να μαθω απεξω τα τριγωνομετρικά (πχ ημπ/6=1/2 ). Ποτε δεν κατάφερα να τα μάθω. Έχετε καμια ιδέα για το πώς να βγαινουν αυτόματα;

aris-bas · 25-02-14

Αρχική Δημοσίευση από styt_geia:
1) Εφαρμογή του θεωρήματος Fermat για την $g(x)=f(x)-e^x+x^2$

2)
i) Είναι $f'(x)=3x^2+2(a-1)x+3$ με διακρίνουσα $\Delta = 4 (a-1)^2-4 \cdot 9$ οπότε η πρόταση «η f δεν έχει ακρότατα» είναι ισοδύναμη με τις προτάσεις
$\Delta \leq 0 \Leftrightarrow (a-1)^2 \leq 9 \Leftrightarrow |a-1| \leq 3 \Leftrightarrow -3 \leq a-1 \leq 3 \Leftrightarrow -2 \leq a \leq 4$
ii)
Έυκολα βρίσκουμε ότι $f(-1)f(-2)<0$ οπότε η f έχει τουλάχιστον μία ρίζα στο διάστημα $(-2,-1)$ . Η f επιπλέον είναι γνησίως αύξουσα για $a=2 \in [-2,4]$ οπότε η προηγούμενη ρίζα είναι και μοναδική.

Ευχαριστώ πολύ

vimaproto · 26-02-14

Αρχική Δημοσίευση από Victoria Hislop:
Έχω ένα μεγάλο πρόβλημα. Οι εξετάσεις πλησιάζουν και εγώ δεν μπορω ακομα να μαθω απεξω τα τριγωνομετρικά (πχ ημπ/6=1/2 ). Ποτε δεν κατάφερα να τα μάθω. Έχετε καμια ιδέα για το πώς να βγαινουν αυτόματα;

γωνία 0° 30° 45° 60° 90°
ημ √0/2 √1/2 √2/2 √3/2 √4/2
συν √4/2 √3/2 √2/2 √1/2 √0/2
Πιστεύω να καταλαβαίνεις τον πίνακα που απομνημονεύεται εύκολα
Για την εφαπτομένει διαιρείς τους δύο αντίστοιχους όρους του ημιτόνου και του συνημιτόνου

Dafni16 · 26-02-14

Kαλησπέρα!!Κάνω επανάληψη στα Μαθηματικά και έχω μία απορία!Όταν έχουμε μία συνάρτηση και ξέρουμε την μονοτονία και τη ρίζα της τότε ξέρουμε πάντα και το πρόσημο!Σωστά?Δηλαδή πείτε που έχουμε μία συνάρτηση f(x) η οποία είναι γνησίως αύξουσα στο R και έχει προφανή ρίζα το 0.Πως βρίσκουμε το προσημο της f(x)?

Effort · 26-02-14

Αφου η συναρτηση σου ειναι γνησιως αυξουσα στο R εχει και πεδιο ορισμου ολο το R.
Aφου η συναρτηση ειναι συνεχης και γνησιως αυξουσα τοτε εχει μοναδικη ριζα.Αρα η προφανης ριζα (που στην προκειμενη περιπτωση ειναι το 0) ειναι και μοναδικη.
Ετσι εχουμε:
-x>0 τοτε αφου η f ειναι γν.αυξουσα προκυπτει οτι f(x)>f(0)=0
-x<0 τοτε αφου η f ειναι γν,αυξουσα προκυπτει οτι f(x)<f(0)=0
-x=0 f(0)=0.
Eτσι εχεις το προσημο της f στο R.

methexys · 26-02-14

λες για παράδειγμα, αν η ρίζα είναι το 0: x<0 => (επειδή f αύξουσα)f(x)<f(0) => f(x)<0
x>0 => (επειδή f αύξουσα) f(x)>f(0) => f(x)>0

Dafni16 · 26-02-14

ok thnx!!!

aris-bas · 27-02-14

παιδια θα ηθελα τη βοηθεια στις παρακατω....
στην 1η ασκηση εχω κολλησει στο (γ) ερωτημα

και στην δευτερη παιρνω τις σχεσεις f(1)=2
f ' (0)=1
f(0)=0
ειναι σωστες ή κανω κατι λαθος??

υ.γ στη δευτερη ασκηση η f(x)=α(χ^3)+β(χ^2)+γχ

Βοήθεια/Aπορίες στα Μαθηματικά Προσανατολισμού

Νεοφερμένος

Πολύ δραστήριο μέλος

Εκκολαπτόμενο μέλος

Περιβόητο μέλος

Πολύ δραστήριο μέλος

Εκκολαπτόμενο μέλος

Πολύ δραστήριο μέλος

Τιμώμενο Μέλος

Πολύ δραστήριο μέλος

Εκκολαπτόμενο μέλος

Νεοφερμένος

Πολύ δραστήριο μέλος

Νεοφερμένος

Νεοφερμένος

Πολύ δραστήριο μέλος

Νεοφερμένος

Εκκολαπτόμενο μέλος

Τιμώμενο Μέλος

Νεοφερμένος

Νεοφερμένος