aris-bas
Νεοφερμένο μέλος


α) Ουσιαστικά ζητάει νδο υπάρχει χ1 ανήκει στο (α,β) ώστε f'(x1)=1
με ΘΜΤ στο (α,β) (επειδή είναι συνεχής και παρ/μη) έχουμε ότι υπάρχει ένα χ1 που ανήκει στο (α,β) ώστε f'(x1)=[f(β)-f(α)]/β-α=(β-α)/(β-α)=1 άρα ισχύει
σχετικά με το β ερώτημα,στο τέλος λέει αβ=4?
edit: τώρα είδα ότι υπάρχει και κώδικας latex,σόρυ!
στο τελος λεει αβ>0 ...συνγωμη για την κακη αναλυση..

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Demlogic
Πολύ δραστήριο μέλος


η δευτερή είναι πολύ εύκολη.
στο α απλά αναπτύσσεις την σχέση με τους μιγαδικούς που σου δίνει στο Α μέλος ( με την ιδιότητα |z|²=zz', με z' τον συζηγή)
και καταλήγεις στο (z1/z2)' = z1/z2
στο β αφου γνωρίζεις οτι z1/z2 ER , θα είναι Im(z1/z2)=0, όπου με λίγες πράξεις βρίσκεις το φανταστικό μέλος f(α)β-αf(β) και το μηδενίζεις
-------------
τωρα για την πρώτη άσκηση το τελευταιο ερώτημα, έχω
αβ>0 αρα α>0 β>0 ή β<0 α<0 με α<β λόγω έννοια διαστήματος ( βλέπε (α,β) )
μια τυχαια εφαπτομένη στο χο εχει τη μορφη y = f'(xo) x - f'(xo) xo + f(xo)
και για να διερχεται αυτη απο την Α.Α. πρεπει f(xo) - f'(xo)xo=0 -> f'(xo)xo - f(xo)=0
αν χο≠0 τότε έχω ( f'(xo) xo - f(xo) xo' )/xo² = 0 κατι που σημαινει οτι (f(xo)/xo)' = 0
ειτε β>α>0 είτε α<β<0, πληρούνται οι προϋποθέσεις του Θ. Rolle για την
f(x)/x στο (α,β)
αφου f(a)/a = a/a = 1 = b/b = f(b)/b
άρα υπάρχει xo τέτοιο ώστε (f(xo)/xo)' = 0 -> μπλα μπλα
Υ.Γ. θεώρησα χωρίς πρόβλημα οτι xo≠0 απο την στιγμή που στο διάστημα [α,β] δεν περιλαμβάνεται το 0
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Μάγδα Μάγδα
Νεοφερμένο μέλος


a) να βρείτε το lim {x->0} f(x)
b) να αποδείξετε ότι το lim {x->0} f(x)/ (ημx)^2 δεν υπάρχει
c) να βρείτε το lim{x->0} (x*f(x) - ημ3x)/ [(x^2 - x +4)^1/2 -2]
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Aristeidis
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


α)Δίνεται η συνάρτηση f:R->R για την οποία ισχύει : 6x-x^2<= f(x)<= x^2+6x , gia kathe xeR
a) να βρείτε το lim {x->0} f(x)
b) να αποδείξετε ότι το lim {x->0} f(x)/ (ημx)^2 δεν υπάρχει
c) να βρείτε το lim{x->0} (x*f(x) - ημ3x)/ [(x^2 - x +4)^1/2 -2]
β)
με
άρα από κριτήριο παρεμβολής
οπότε πάλι με την ίδια διαδικασία βρίσκουμε
γ)
οπότε
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Aristeidis
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
methexys
Τιμώμενο Μέλος


a) μπορείς να το κάνεις με πράξεις f(x1)=f(x2)....x1=x2 ή να δοκιμάσεις με μονοτονία, ώστε να βρεις αν η f είναι γν αυξουσα η φθινουσα
f-1(x)=0 => f(f-1(x))=f(0) => x=f(0) => x=1
b) πρέπει να βρεις το σύνολο τιμών
γ) (0,5)^χ-χ^3=1 => f(x)=1 προφανής ρίζα το 0 και επειδή η f είναι φθίνουσα θα είναι και μοναδική ρίζα
ελπίζω να καταλαβαίνεις τι γραφω και να μην έχω γράψει καμιά κοτσάνα, διαβάζω πολλή φυσική τις τελευταίες μέρες και είμαι λίγο εκτός κλίματος

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Aristeidis
Νεοφερμένο μέλος



Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Το πρώτο ερώτημα είναι απλές πράξεις:Και η άλλη. Ευχαριστώ εκ των προτέρων!
κλπ. Για το δεύτερο ερώτημα παρατήρησε ότι
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Aristeidis
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
meletis96
Νεοφερμένο μέλος


ο τυπος της f και να δειχθεί ότι η εξισωση f(χ)=0 εχει μοναδικη ρίζα στο (ο ,+οο). Mπορει κάποιος να με βοηθησει? ευχαριστω
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Gabriel97
Νεοφερμένο μέλος


α. Το μέσο Μ της πλευράς ΒΓ
β. Την εξίσωση της πλευράς ΒΓ
2. Δίνεται τρίγωνο ΑΒΓ με Α ( 2,1 ) και 3χ+Ψ-11=0 , χ-ψ+3=0 είναι οι εξισώσεις δύο υψών του.
α. Να βρεθεί το ορθόκεντρο Η
β. Να βρεθουν οι κοριφές Β,Γ
γ.Να βρεθούν οι εξισώσεις των πλευρών του .
δ. Να βρεθεί το εμβαδόν του τριγώνου.
3. Για διακεκριμένα σημεία Α,Β,Γ ισχύει 4ΟΑ+ΓΑ=3ΟΒ+ΟΓ ( ΟΑ,ΓΑ,ΟΒ,ΟΔ διανύσματα )
α. Να δείξετε ότι τα σημεία Α,Β,Γ ανήκουν στην ίδια ευθεία
Β. Να βρείτε τη σχετική θέση των Α,Β,Γ πάνω στην ε
γ. Αν Μ μέσο του ΑΓ να βρείτε την τιμή του Χ, ώστε να ισχύει ΑΜ ( διάνυσμα ) = χ * ΑΒ ( διάνυσμα ) και το Μ να είναι μέσο του ΑΓ
4.Δίνεται τρίγωνο ΑΒΓ με Α(-1,2) , Β(7,0) ΚΑΙ Γ (1,4) . Αν Δ το μέσο διαμέσου ΑΜ και για το σημείο Ε ισχύει 2ΑΕ( διάνυσμα ) = ΕΓ (διάνυσμα )
α. Να βρείτε τα σημεία Δ, Ε
Β. Να αποδείξετε ότι τα σημεία Β,Δ,Ε είναι συνευθειακά
παρακαώ αν μπορείτε να έχετε απαντήσει μέχρι και τις 05/01/2014
Τα έχω μπερδέψει τελείως

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
methexys
Τιμώμενο Μέλος


f(x/e) <= lnx <= f(x)-1
f(x/e) <= lnx
θέτω x/e=ψ>0 άρα f(ψ)<=ln(eψ) => f(x)<= lne + lnx => f(x)<= 1+lnx 1η σχεση)
και τωρα παιρνεις το αλλο μελος
lnx <= f(x) -1 => lnx+1 <= f(x) 2η σχεση)
απο 1 και 2, συμφωνα με την αντισυμμετρικη ιδιοτητα, f(x)=lnx + 1
f(x)=0 => lnx=-1 => e^{-1}=x
f'(x)= 1/x >0 επειδή x ανήκει στο 0,+οο άρα f γν. αύξουσα άρα η ρίζα που βρήκαμε είναι μοναδική
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


1.1. Δίνεται τρίγωνο ΑΒΓ με Α ( -1,2) , ορθόκεντρο Η(3,0) και βαρύκεντρο θ(1,4). Να βρείτε :
α. Το μέσο Μ της πλευράς ΒΓ
β. Την εξίσωση της πλευράς ΒΓ
2. Δίνεται τρίγωνο ΑΒΓ με Α ( 2,1 ) και 3χ+Ψ-11=0 , χ-ψ+3=0 είναι οι εξισώσεις δύο υψών του.
α. Να βρεθεί το ορθόκεντρο Η
β. Να βρεθουν οι κοριφές Β,Γ
γ.Να βρεθούν οι εξισώσεις των πλευρών του .
δ. Να βρεθεί το εμβαδόν του τριγώνου.
3. Για διακεκριμένα σημεία Α,Β,Γ ισχύει 4ΟΑ+ΓΑ=3ΟΒ+ΟΓ ( ΟΑ,ΓΑ,ΟΒ,ΟΔ διανύσματα )
α. Να δείξετε ότι τα σημεία Α,Β,Γ ανήκουν στην ίδια ευθεία
Β. Να βρείτε τη σχετική θέση των Α,Β,Γ πάνω στην ε
γ. Αν Μ μέσο του ΑΓ να βρείτε την τιμή του Χ, ώστε να ισχύει ΑΜ ( διάνυσμα ) = χ * ΑΒ ( διάνυσμα ) και το Μ να είναι μέσο του ΑΓ
4.Δίνεται τρίγωνο ΑΒΓ με Α(-1,2) , Β(7,0) ΚΑΙ Γ (1,4) . Αν Δ το μέσο διαμέσου ΑΜ και για το σημείο Ε ισχύει 2ΑΕ( διάνυσμα ) = ΕΓ (διάνυσμα )
α. Να βρείτε τα σημεία Δ, Ε
Β. Να αποδείξετε ότι τα σημεία Β,Δ,Ε είναι συνευθειακά
παρακαώ αν μπορείτε να έχετε απαντήσει μέχρι και τις 05/01/2014
Τα έχω μπερδέψει τελείως
α) Αν
και εξισώνοντας τις συντεταγμένες, βρίσκεις τα
β) Η ευθεία ΒΓ είναι κάθετη στο ύψος ΑΗ οπότε ξέρεις τον συντελεστή διεύθυνσης της ΒΓ. Επιπλέον ξέρεις και ένα σημείο της ΒΓ, το Μ από το προηγούμενο ερώτημα. Με βάση αυτά μπορείς να βρεις την εξίσωση της ΒΓ.
2.
Κατ' αρχάς οι συντεταγμένες του Α δεν επαληθεύουν καμία από τις εξισώσεις των υψών. Άρα οι εξισώσεις αυτές είναι των υψών που διέρχονται από τα σημεία Β και Γ. Έστω Ε το σημείο που το ύψος από το Γ τέμνει την ΑΒ και Δ το σημείο που το ύψος από το Β τέμνει την ΑΓ. Ας θεωρήσουμε χωρίς βλάβη της γενικότητας ότι η εξίσωση της ΓΕ ειναι η
α) Από την λύση του συστήματος των εξισώσεων των δύο υψών βρίσκεις τις συντεταγμένες του Η.
β) Η ΑΒ είναι κάθετη στην ΓΕ άρα ξέρεις τον συντελεστή διεύθυνσής της. Επιπλέον ξέρεις τις συντεταγμένες του Α οπότε μπορείς να βρεις την εξίσωση της ΑΒ. Αντίστοιχα η ΑΓ είναι κάθετη στην ΒΔ άρα ξέρεις τον συντελεστή διεύθυνσής της. Επιπλέον ξέρεις τις συντεταγμένες του Α οπότε μπορείς να βρεις την εξίσωση της ΑΓ.
Από την λύση του συστήματος των ΑΒ και ΒΔ βρίσκεις το Β και από την λύση του συστήματος των ΑΓ και ΕΓ βρίσκεις το Γ.
γ) Έχεις ήδη βρει τις δύο πλευρές στο ερώτημα β) και μένει μόνο η εξίσωση της ΒΓ η οποία είναι εύκολη αφού ξέρεις τα Β και Γ.
δ) Άμεση εφαρμογή του τύπου
3.
α)
Από την τελευταία σχέση προκύπτει ότι τα Α,Β,Γ είναι συνευθειακά.
β) Επειδή τα
γ) Είναι
όμως από το ερώτημα α) βρήκαμε
Και υποθέτωντας ότι τα Α και Β δεν συμπίπτουν, από την παραπάνω σχέση είναι
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Μάγδα Μάγδα
Νεοφερμένο μέλος


α)
(άμεσο από κριτήριο παρεμβολής)
β)
Για
και κοντά στο
είναι:
με
άρα από κριτήριο παρεμβολής
και αφού
για
και κοντά στο
, έχουμε
Ανάλογα για
και κοντά στο
είναι:
οπότε πάλι με την ίδια διαδικασία βρίσκουμεοπότε το όριο δεν υπάρχει αφού τα πλευρικά όρια δεν συμπίπτουν.
γ)
οπότε
=12)
styt_geia ευχαριστώ για την απάντηση! ωστόσο, δεν καταλαβαίνω καθόλου πως έλυσες το δεύτερο ερώτημα... γιατί το μηδενικό στην ανίσωση? πως προέκυψε?
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Gabriel97
Νεοφερμένο μέλος


1.
α) Αντο μέσο της ΒΓ τότε λόγω της γνωστής ιδιότητας του βαρυκέντρου, ισχύει
και εξισώνοντας τις συντεταγμένες, βρίσκεις τα
β) Η ευθεία ΒΓ είναι κάθετη στο ύψος ΑΗ οπότε ξέρεις τον συντελεστή διεύθυνσης της ΒΓ. Επιπλέον ξέρεις και ένα σημείο της ΒΓ, το Μ από το προηγούμενο ερώτημα. Με βάση αυτά μπορείς να βρεις την εξίσωση της ΒΓ.
2.
Κατ' αρχάς οι συντεταγμένες του Α δεν επαληθεύουν καμία από τις εξισώσεις των υψών. Άρα οι εξισώσεις αυτές είναι των υψών που διέρχονται από τα σημεία Β και Γ. Έστω Ε το σημείο που το ύψος από το Γ τέμνει την ΑΒ και Δ το σημείο που το ύψος από το Β τέμνει την ΑΓ. Ας θεωρήσουμε χωρίς βλάβη της γενικότητας ότι η εξίσωση της ΓΕ ειναι ηκαι ότι η εξίσωση της ΒΔ είναι η
.
α) Από την λύση του συστήματος των εξισώσεων των δύο υψών βρίσκεις τις συντεταγμένες του Η.
β) Η ΑΒ είναι κάθετη στην ΓΕ άρα ξέρεις τον συντελεστή διεύθυνσής της. Επιπλέον ξέρεις τις συντεταγμένες του Α οπότε μπορείς να βρεις την εξίσωση της ΑΒ. Αντίστοιχα η ΑΓ είναι κάθετη στην ΒΔ άρα ξέρεις τον συντελεστή διεύθυνσής της. Επιπλέον ξέρεις τις συντεταγμένες του Α οπότε μπορείς να βρεις την εξίσωση της ΑΓ.
Από την λύση του συστήματος των ΑΒ και ΒΔ βρίσκεις το Β και από την λύση του συστήματος των ΑΓ και ΕΓ βρίσκεις το Γ.
γ) Έχεις ήδη βρει τις δύο πλευρές στο ερώτημα β) και μένει μόνο η εξίσωση της ΒΓ η οποία είναι εύκολη αφού ξέρεις τα Β και Γ.
δ) Άμεση εφαρμογή του τύπου
3.
α)
Από την τελευταία σχέση προκύπτει ότι τα Α,Β,Γ είναι συνευθειακά.
β) Επειδή τακαι
είναι αντίρροπα, συμπεραίνουμε ότι το Α βρίσκεται μεταξύ των Β και Γ.
γ) Είναικαι
οπότε
,
όμως από το ερώτημα α) βρήκαμε. Από (1) και (2) είναι
Και υποθέτωντας ότι τα Α και Β δεν συμπίπτουν, από την παραπάνω σχέση είναι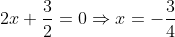
Σας ευχαριστώ πάρα πολύ !!
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Gabriel97
Νεοφερμένο μέλος


α. Να βρείτε τις συντεταγμένες των διανυσμάτων ΑΒ και ΑΓ
β. Να αποδείξετε ότι τα σημεία Α , Β , Γ είναι συνευθειακα
γ. Να βρείτε τη σχετική θέση των Α,Β,Γ
2. Δίνεται τρίγωνο ΑΒΓ με Α(-1,0) , Β (2,-3) και Γ(0,1)
Να βρείτε το διάνυσμα ν για το οποίο ισχύει:
2ν=ΑΒ-|ν|*ΑΓ (ν,ΑΒ,ΑΓ διανύσματα )
3. Δίνεται πετιτή , γνησίως μονότονη συνάρτηση φ, με πεδίο ορισμού το R και σύνολο τιμών το R , όπου η γραφική της παράσταση διέρχεται απο το Α(1,4) και Β(2,3)
α. Να αποδείξεται ότι η φ, είναι γνησίως φθίνουσα
β. Να λυθεί η ανίσωση φ(χ-3)<4γ
γ. Να αποδείξετε ότι
φ(-χ^2 - 1) + φ(χ^2+1)= 0 για κάθε χ e R
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Πχ στο δεξί πλευρικό όριο, γιαstyt_geia ευχαριστώ για την απάντηση! ωστόσο, δεν καταλαβαίνω καθόλου πως έλυσες το δεύτερο ερώτημα... γιατί το μηδενικό στην ανίσωση? πως προέκυψε?
κλπ. Η πιο απλά σκέψου δύο θετικούς αριθμούς πχ
Βασικά θα μπορούσα να αντιστρέψω όλη την ανισότητα και να γράψω
κτλ. Το όριο της μεσαίας πάλι 0 θα βγει από κ. παρεμβολής.
Απλά επέλεξα τον πρώτο τρόπο για να δείξω ότι χρειαζόμαστε μόνο την μία ανισότητα αλλά και για να φαίνεται καλύτερα το πρόσημο της
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Aristeidis
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 1 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 231 μέλη διάβασαν αυτό το θέμα:
- ChrisG152
- giorgos5002
- giannis06
- Panagiwths12
- mikke
- hristosdab
- trifasikodiavasma
- haji
- thepigod762
- Mariosm.
- soulatso
- oteletampis
- phleidhs
- AggelikiGr
- sir ImPeCaBlE
- veiNqh
- Scandal
- alekos
- Debugging_Daemon
- just some guy
- xristosgkm
- ismember
- Apocalypse
- arrow25
- rempelos42
- ggl
- GStef
- QWERTY23
- xrisamikol
- Σωτηρία
- nikoletaz57
- _Aggelos123
- Mariam38
- SlimShady
- strsismos88
- Georgekk
- Lia 2006
- igeorgeoikonomo
- marian
- tsiobieman
- constansn
- Xristosdimitra
- Panagiotis849
- ρενακι 13
- Memetchi
- eukleidhs1821
- Nikkkpat
- Unboxholics
- korlef
- kwstaseL
- Thanos_D
- the purge
- T C
- Giii
- Papachrist
- liaiscool
- Αννα Τσιτα
- globglogabgalab
- Pharmacist01
- otinanai123
- abcdefg12345
- nicole1982
- thecrazycretan
- kvstas92
- KingOfPop
- maria301
- papa2g
- stefan
- Κλημεντίνη
- TonyMontanaEse
- Lathy
- Alexecon1991
- Μάρκος Βασίλης
- Cortes
- το κοριτσι του μαη
- calliope
- ale
- panagiotis G
- Kleanth
- aggelosst9
- BioChemical
- spring day
- nucomer
- Georgia110
- LeoDel
- pink_panther
- Alexandros973
- marsenis
- den antexw allh apotyxia
- KaterinaL
- kiyoshi
- drosos
- Λαμπρινηη
- Bill22
- Chrysablac.
- giorgosp97
- Βλα
- Monster Hunter
- jul25
- xxxtolis
- Stroka
- nicks1999
- totiloz
- Earendil
- mitsakos
- tasost
- lnesb
- ssalex
- alan09
- Livaja10
- χημεια4λαιφ
- Viedo
- UncleJ
- Kostakis45
- Infrared
- Zgian
- pepatogourounaki
- hirasawayui
- GeoCommand
- Eleni54
- American Economist
- EiriniS20
- ΘανάσοςG4
- stamoul1s
- Αριάνα123
- uni77
- Libertus
- tasoss
- PanosCh002
- Unseen skygge
- Νικόλας Ραπ.
- cel123
- The Limit Does Not Exist
- don_vito
- suaimhneas
- Αλκης Κ.
- alexrami
- Baggelitsa36
- Νομικάριος13
- spinalgr1990
- d_th
- Adolfo valencia
- Πα.Κ
- Vasilis25
- Johnman97
- Steffie88
- rekcoR
- gwgw_5
- fockos
- Mariahj
- roud
- kostas83
- Cpt.Philips
- Makis45
- Χρησλου
- Panos_02
- Vold
- tymvorixos
- GiorgosAsi
- Neos167
- theodoraooo
- George187
- Άρτεμις Α.
- Μαρία2222
- christos87
- Idontknoww
- jimis2001
- Metamorph
- Γατόπαρδος.
- Johnsk
- mitsos14
- johnsiak
- Elel
- Dreamer_SW
- Γιαννης1987Θεσσ
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki




