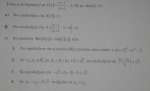Guest 018946
Επισκέπτης


Αν κατάλαβα καλά λες: Έστω. Αρκεί να δείξω ότι η εξίσωση
έχει τουλάχιστον μία λύση ως προς
. Έστω λοιπόν
μία λύση της (1). Τότε για
στην δοσμένη έχουμε
Μέχρι στιγμής έχω δείξει ότι αν η (1) έχει λύση τότε αυτή θα είναι ηπου βρήκα. Μένει όμως και το αντίστροφο. Πρέπει να επαληθεύσουμε δηλαδή ότι για
είναι πράγματι
=y)
για να ειμαστε ακριβεις δεν θεωρησα οτι υπαρχει αυτο το χ0 αλλα εβαλα οπου φ(χ) το ψ στην συναρτησιακη και μετα ελυσα ως προς χ ( δεν ηξερα οτι χρειαζεται σε αυτες τις ασκησεις και επαληθευση )
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
mary1269
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Lost in the Fog
Νεοφερμένο μέλος


α)θα ηθελα λιγη βοηθεια με την παρακατω ασκηση
β)
Εφαρμόζω τριγωνική ανισότητα στο
γ)1.
Βρίσκεις τα Re(f(z)) και Im(f(z)), τα εξισώνεις και καταλήγεις στη σχέση :
2.
3.
Από την εξίσωση κύκλου προκύπτει :
4.
Η τριγωνική ανισότητα στο |z1+z2| εφαρμόζεται κατά τον ίδιο τρόπο στο |z1-z2|.Όπως στο γ)2. από τριγωνική στο |z1-z2|:
Για το τελευταίο δεν είμαι καθόλου σίγουρος. Όποιος ξέρει ας διορθώσει ή επαληθεύσει.
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χαράλαμπος μβ
Νεοφερμένο μέλος



Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Lost in the Fog
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
panabarbes
Εκκολαπτόμενο μέλος


Να βρείτε συνάρτηση f ορισμένη στο (-π/2,π/2) για την οποία ισχύουν f(0)=2012 και συνx f'(x)+ημx f(x) = xσυνχσυνχ για κάθε χεR.
!
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Συνημμένα
M@r!@n@
Νεοφερμένο μέλος


Εφόσον η συνάρτηση f είναι ορισμένη και παραγωγίσιμη στο R και αφού η συνάρτηση g(x)=x+x^3 είναι ορισμένη και παραγωγίσιμη στο R ως πολυωνυμική, τότε ορίζεται και είναι παραγωγίσιμη στο R η σύνθεση των f και g.Επίσης, η πολυωνυμική στο δεξί μέλος είναι ορισμένη και παραγωγίσιμη στο R. Επομένως παραγωγίζοντας την σχέση κατά μέλη προκύπτει:
f'(x+x^3)(3x²+1)=3x² , για κάθε xεR
Επομένως για x=1: 4f'(2)=3 άρα f'(2)=3/4
ευχαριστωω! μας την ειχε βάλει καταλάθος δεν είχαμε προχωρήσει μέχρι συνθετες

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 018946
Επισκέπτης


Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
tipotas
Εκκολαπτόμενο μέλος



Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Schoolmate
Εκκολαπτόμενο μέλος




Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Schoolmate
Εκκολαπτόμενο μέλος


Στην φωτογραφία την πρώτη προς το τέλος στο πάνω σημείο είναι το Β δεν φαίνεται και από κάτω το Γ. Από την Β στην Α λέει υπάρχουν 0 τρόποι, ενώ κανονικά είναι ΒΑΒ δηλαδή ένας τρόπος, στην φωτογραφία 2 έχουνε βάλει 0 τρόπους , όπως και σε άλλα σημεία έχει λάθη.
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
giwrgossp
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rolingstones
Πολύ δραστήριο μέλος


f(f(x))=3x+2 Βρες αντιστροφη
( αποψη μου ειναι πως δεν μπορουμε να την βρουμε )
μην βιαζεσαι η ασκηση ειναι πολυ απλη στο απαντησα πιο πανω
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 018946
Επισκέπτης


Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Schoolmate
Εκκολαπτόμενο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Maria_Spring
Νεοφερμένο μέλος
rebel
Πολύ δραστήριο μέλος


Από κ. παρεμβολής είναι
από κ. παρεμβολής
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 10 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 227 μέλη διάβασαν αυτό το θέμα:
- hristosdab
- trifasikodiavasma
- haji
- thepigod762
- Mariosm.
- soulatso
- oteletampis
- phleidhs
- Hased Babis
- AggelikiGr
- sir ImPeCaBlE
- veiNqh
- Scandal
- alekos
- Debugging_Demon
- just some guy
- xristosgkm
- ismember
- Apocalypse
- arrow25
- rempelos42
- ggl
- GStef
- QWERTY23
- xrisamikol
- Σωτηρία
- nikoletaz57
- _Aggelos123
- Mariam38
- SlimShady
- strsismos88
- Georgekk
- Lia 2006
- igeorgeoikonomo
- marian
- tsiobieman
- constansn
- Xristosdimitra
- Panagiotis849
- ρενακι 13
- Memetchi
- eukleidhs1821
- Nikkkpat
- Unboxholics
- korlef
- kwstaseL
- Thanos_D
- the purge
- T C
- Giii
- Papachrist
- liaiscool
- Αννα Τσιτα
- globglogabgalab
- Pharmacist01
- thanahss
- abcdefg12345
- nicole1982
- thecrazycretan
- kvstas92
- KingOfPop
- maria301
- papa2g
- stefan
- Κλημεντίνη
- TonyMontanaEse
- Athens2002
- Alexecon1991
- Μάρκος Βασίλης
- Cortes
- το κοριτσι του μαη
- calliope
- ale
- panagiotis G
- Kleanth
- aggelosst9
- BioChemical
- spring day
- nucomer
- Georgia110
- LeoDel
- pink_panther
- Alexandros973
- marsenis
- den antexw allh apotyxia
- KaterinaL
- kiyoshi
- drosos
- Λαμπρινηη
- Bill22
- Chrysablac.
- giorgosp97
- Βλα
- Monster Hunter
- jul25
- xxxtolis
- Stroka
- nicks1999
- totiloz
- Earendil
- mitsakos
- tasost
- lnesb
- ssalex
- Vasilina93
- alan09
- Livaja10
- χημεια4λαιφ
- Viedo
- UncleJ
- Kostakis45
- Infrared
- Zgian
- pepatogourounaki
- hirasawayui
- GeoCommand
- Eleni54
- American Economist
- EiriniS20
- ΘανάσοςG4
- stamoul1s
- Αριάνα123
- uni77
- Libertus
- tasoss
- PanosCh002
- Unseen skygge
- Νικόλας Ραπ.
- cel123
- The Limit Does Not Exist
- don_vito
- suaimhneas
- Αλκης Κ.
- alexrami
- Baggelitsa36
- Νομικάριος13
- spinalgr1990
- d_th
- Adolfo valencia
- Πα.Κ
- Vasilis25
- Johnman97
- Steffie88
- rekcoR
- gwgw_5
- fockos
- Mariahj
- roud
- kostas83
- Cpt.Philips
- Makis45
- Χρησλου
- Panos_02
- Vold
- tymvorixos
- GiorgosAsi
- Neos167
- theodoraooo
- George187
- Άρτεμις Α.
- Μαρία2222
- christos87
- Idontknoww
- jimis2001
- Metamorph
- Γατόπαρδος.
- Johnsk
- mitsos14
- johnsiak
- Elel
- Dreamer_SW
- Γιαννης1987Θεσσ
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki