καλησπερα!θα ηθελα τη βοηθεια σας στις παρακατω ασκησεις:
1)δινεται η συναρτηση
 =xlnx-\lambda x+1,\quad \lambda \quad \in \quad R)
α)να βρειτε την ελαχιστη τιμη της f
β)να βρειτε το γεωμετρικο τοπο των σημειων Μ(x,f(x)) οπου χ η θεση ελαχιστου της f
γ)να βρειτε τη μεγαλυτερη τιμη του λ για την οποια ισχυει
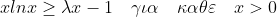
δ)για τη μεγαλυτερη τιμη του λ που θα βρειτε παραπανω ,να αποδειξετε οτι η ευθεια
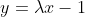
εφαπτεται της γραφικης παραστασης της συναρτησης
 =xlnx)
α) Η συνάρτηση f είναι συνεχής και παραγωγίσιμη στο (0,+οο) με πρώτη παράγωγο
f΄(x)=lnx+1-λ, x>0
f΄(x)=0 <=> lnx+1-λ=0 <=> lnx=λ-1 <=> x=e^(λ-1)
Η f είναι συνεχής στο (0,e^(λ-1)], παραγωγίσιμη στο (0,e^(λ-1)) και ισχύει f΄(x)<0 για κάθε x στο (0,e^(λ-1)). Άρα η f είναι γνησίως φθίνουσα στο (0,e^(λ-1)]. Η f είναι συνεχής στο [e^(λ-1),+οο), παραγωγίσιμη στο (e^(λ-1),+οο) και ισχύει f΄(x)>0 για κάθε x στο (e^(λ-1),+οο). Άρα η f είναι γνησίως αύξουσα στο [e^(λ-1),+οο).
Η f είναι συνεχής στο (0,+οο), γνησίως φθίνουσα στο (0,e^(λ-1)] και γνησίως αύξουσα στο [e^(λ-1),+οο). Επομένως η f παρουσιάζει ολικό ελάχιστο στο x0=e^(λ-1) με τιμή f(x0)=f(e^(λ-1))=1-(e^(λ-1))
β) Το σημείο Μ(x,y) ελαχίστου της Cf έχει συντεταγμένες:
x=e^(λ-1)
y=1-(e^(λ-1))
όπου λ ανήκει R
Άρα y=1-x. Επομένως το σημείο Μ βρίσκεται στην ευθεία (ε) y=-x+1 για τις διάφορες τιμές του λ ανήκει R.
γ) Έχουμε:
xlnx>=λx-1 <=> xlnx-λx+1>=0 <=> f(x)>=0 για κάθε x>0
Εφόσον η f παρουσιάζει ολικό ελάχιστο στο x0 τότε ισχύει f(x)>=f(x0) για κάθε x>0. Επομένως για να ισχύει f(x)>=0 για κάθε x>0 πρέπει να ισχύει f(x0)>=0. Έχουμε:
f(x0)=1-(e^(λ-1))=h(λ) όπου λ ανήκει R. Επομένως πρέπει να ισχύει g(λ)>=0
Η συνάρτηση h είναι συνεχής και παραγωγίσιμη στο R με πρώτη παράγωγο h΄(λ)=-e^(λ-1)<0 για κάθε λ ανήκει R.
Η h είναι συνεχής και παραγωγίσιμη στο R και ισχύει h΄(λ)<0 για κάθε λ ανήκει R. Άρα η h είναι γνησίως φθίνουσα στο R.
Έχουμε h(1)=0.
λ<1 => h(λ)>h(1) =>h(λ)>0
λ>1 => h(λ)<h(1) => h(λ)<0
Επομένως για λ<=1 ισχύει h(λ)>=0. Η μέγιστη τιμή του λ για την οποία f(x)>=0 για κάθε x>0 είναι η λmax=1.
δ) Για λ=1 η ευθεία είναι η (ζ) y=x-1
Η g είναι συνεχής και παραγωγίσιμη στο (0,+οο) με πρώτη παράγωγο g΄(x)=lnx+1, x>0
Θα προσδιορίσουμε την εφαπτομένη της Cg στο σημείο A(1,g(1)). Έχουμε g(1)=0 και g΄(1)=1. Συνεπώς
y-g(1)=g΄(1)(x-1) <=> y-0=1*(x-1) <=> y=x-1
Άρα η (ζ) είναι εφαπτομένη της Cg στο σημείο Α(1,g(1)).


 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

 )
)
 (νομίζω)
(νομίζω)
