1)Εστω μια συναρτηση
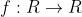
η οποια ειναι παραγωγισιμη και ισχυει
+f(x)={e}^{x}-x+1)
για καθε x που ανηκει στο R. Να εξετασετε την f ως προς τη μονοτονια και τα ακροτατα.
Θεωρούμε τη συνάρτηση g(x)=(x^3)+x, x ανήκει Dg=R. Η g είναι συνεχής και παραγωγίσιμη στο R με πρώτη παράγωγο:
g΄(x)=3(x^2)+1>=1>0 για κάθε x ανήκει R.
Η g είναι συνεχής και παραγωγίσιμη στο R με f΄(x)>0 για κάθε x ανήκει R. Άρα η g είναι γνησίως αύξουσα στο R, άρα και 1-1. Επομένως ισχύει η ισοδυναμία:
y=g(x) <=> x=(g-1)(y) για κάθε x ανήκει Dg=R, y ανήκει g(Dg)=R
Είναι g(1)=2 <=> (g-1)(2)=1
lim(x->-oo)g(x)=lim(x->-oo)[(x^3)+x]=lim(x->-oo)(x^3)=-oo
lim(x->+oo)g(x)=lim(x->+oo)[(x^3)+x]=lim(x->-oo)(x^3)=+oo
Η g είναι συνεχής και γνησίως αύξουσα στο R, οπότε g(Dg)=g(R)=(lim(x->-oo)g(x),lim(x->+oo)g(x))=(-oo,+oo)=R
Θεωρούμε την σύνθεση (gof)(x)=g(f(x))=[f(x)^3]+f(x). Για να ορίζεται η gof πρέπει x ανήκει Df=R και f(x) ανήκει Dg=R. Άρα Dgof=R. Επειδή η f είναι παραγωγίσιμη στο Df=R και η g είναι παραγωγίσιμη στο f(Df) υποσύνολο του R τότε η gof είναι παραγωγίσιμη στο R με πρώτη παράγωγο:
(gof)΄(x)=g΄(f(x))f΄(x)=[3(f(x)^2)+1]f΄(x), x ανήκει R
Θεωρούμε την συνάρτηση h(x)=(e^x)-x+1, x ανήκει Dh=R. Η h είναι συνεχής και παραγωγίσιμη στο R με πρώτη παράγωγο:
h΄(x)=(e^x)-1. Έχουμε h΄(0)=0.
Η h είναι συνεχής στο (-οο,0], παραγωγίσιμη στο (-οο,0) και ισχύει h΄(x)<0 για κάθε x ανήκει (-οο,0). Άρα η h είναι γνησίως φθίνουσα στο (-οο,0]. Η h είναι συνεχής στο [0,+οο), παραγωγίσιμη στο (0,+οο) και ισχύει h΄(x)>0 για κάθε x ανήκει (0,+οο). Άρα η h είναι γνησίως αύξουσα στο [0,+οο).
Η h είναι συνεχής στο R, γνησίως φθίνουσα στο (-οο,0] και γνησίως αύξουσα στο [0,+οο). Άρα η f παρουσιάζει ολικό ελάχιστο στο x0=0 με τιμή h(0)=2
h(x)>=h(0) <=> h(x)>=2>0 για κάθε x ανήκει R
Η εξίσωση [f(x)^3]+f(x)=(e^x)-x+1 γράφεται ισοδύναμα
(gof)(x)=h(x) <=> g(f(x))=h(x) για κάθε x ανήκει R
Επομένως
(gof)΄(x)=h΄(x) <=> [3(f(x)^2)+1]f΄(x)=h΄(x) <=> f΄(x)=h΄(x)/ [3(f(x)^2)+1]=[(e^x)-1]/[3(f(x)^2)+1]
Η f είναι συνεχής στο (-οο,0], παραγωγίσιμη στο (-οο,0) και ισχύει f΄(x)<0 για κάθε x ανήκει (-οο,0). Άρα η f είναι γνησίως φθίνουσα στο (-οο,0]. Η f είναι συνεχής στο [0,+οο), παραγωγίσιμη στο (0,+οο) και ισχύει f΄(x)>0 για κάθε x ανήκει (0,+οο). Άρα η f είναι γνησίως αύξουσα στο [0,+οο).
Η f είναι συνεχής στο R, γνησίως φθίνουσα στο (-οο,0] και γνησίως αύξουσα στο [0,+οο). Άρα η f παρουσιάζει ολικό ελάχιστο στο x0=0.
Για x=0 έχουμε
g(f(0))=h(0) <=> f(0)=(g-1)(h(0)) <=> f(0)=(g-1)(2) <=> f(0)=1
Άρα f(x)>=f(0) <=> f(x)>=1 για κάθε x ανήκει R.


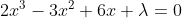 ,
, 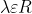
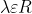 η εξισωση εχει μονο μια ριζα
η εξισωση εχει μονο μια ριζα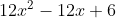 και μετα τη 2η
και μετα τη 2η 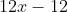 αρα εχω οτι η 1η παραγωγος ειναι γνησιως αυξουσα για καθε x>1 Μετα τι κανω για να δειξω τα παραπανω??
αρα εχω οτι η 1η παραγωγος ειναι γνησιως αυξουσα για καθε x>1 Μετα τι κανω για να δειξω τα παραπανω?? Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki
 1)Εστω μια συναρτηση
1)Εστω μια συναρτηση 

 . Λοιπόν η άσκηση έχει ως εξής: Δίνεται τετράγωνο ΑΒΓΔ με Α(-2,4) και Γ(1,2). Βρείτε τις άλλες δύο κορυφές του. Παρακαλώ απαντήστε μου σύντομα.
. Λοιπόν η άσκηση έχει ως εξής: Δίνεται τετράγωνο ΑΒΓΔ με Α(-2,4) και Γ(1,2). Βρείτε τις άλλες δύο κορυφές του. Παρακαλώ απαντήστε μου σύντομα.