Έχω την παρακάτω άσκηση την οποία έλυσα απλώς θέλω να τσεκάρω λύσεις. Το β,γ αναλυτικά παρακαλώ

Μια συνάρτηση
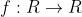
έχει την ιδιότητα:
\leq x^2-3x+2\leq f(x-3)+2x-4)
Έστω μεταβλητή ευθεία η οποία διέρχεται απο το σημείο
)
και τέμνει τη
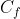
σε δύο διαφορετικά σημεία Α και Β.
α) Να βρεθεί ο τύπος της f
β) Να αποδειχθεί ότι οι εφαπτόμενες της
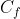
στα Α,Β τέμνονται κάθετα.
γ) Να αποδειχθεί ότι το σημείο τομής των παραπάνω εφαπτομένων κινείται στην σταθερή ευθεία με εξίσωση
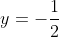
(α) Για κάθε x ανήκει R ισχύει f(x-2)<=(x^2)-3x+2. Επομένως έχουμε:
f((x+2)-2)<=((x+2)^2)-3(x+2)+2 <=> f(x)<=(x^2)+4x+4-3x-6+2 <=> f(x)<=(x^2)+x, x ανήκει R
Για κάθε x ανήκει R ισχύει f(x-3)+2x-4>=(x^2)-3x+2 <=> f(x-3)>=(x^2)-5x+6. Επομένως έχουμε:
f((x+3)-3)>=((x+3)^2)-5(x+3)+6 <=> f(x)>=(x^2)+6x+9-5x-15+6 <=> f(x)>=(x^2)+x, x ανήκει R
Επειδή (x^2)+x<=f(x)<=(x^2)+x για κάθε x ανήκει R τότε f(x)=(x^2)+x=x(x+1) για κάθε x ανήκει R.
Η συνάρτηση f είναι συνεχής και παραγωγίσιμη στο R ως πολυωνυμική με πρώτη παράγωγο f΄(x)=2x+1.
(β) Εφόσον η ευθεία (ζ) τέμνει την Cf σε δύο διαφορετικά σημεία A(x1,f(x1)), B(x2,f(x2)) με x1<x2 τότε η ευθεία (ζ) δεν είναι κατακόρυφη. Επομένως αν η ευθεία (ζ) έχει συντελεστή διεύθυνσης λ και διέρχεται από το σημείο (0,β) τότε έχει εξίσωση της μορφής:
(ζ): y=λx+β
Η (ζ) διέρχεται από το Μ(-1/2,0) οπότε έχουμε:
0=λ*(-1/2)+β <=> β=λ/2
Επομένως η εξίσωση της (ζ) έχει τη μορφή:
(ζ): y=λx+λ/2 <=> y=λ(x+(1/2)), λ ανήκει R
Για να βρούμε τα σημεία τομής της Cf με την (ζ) λύνουμε την εξίσωση y=f(x) όπου y=λ(x+(1/2)). Έχουμε:
f(x)=λ(x+(1/2)) <=> (x^2)+x=λx+(λ/2) <=> (x^2)+(1-λ)x-(λ/2)=0 <=> 2(x^2)+2(1-λ)x-λ=0
Η διακρίνουσα της παραπάνω εξίσωσης είναι:
Δ=[(2(1-λ))^2]-4*2*(-λ)=4((λ^2)+1)>0 για κάθε λ ανήκει R => SQRT(Δ)=2SQRT((λ^2)+1)
Άρα η εξίσωση f(x)=y έχει για κάθε λ ανήκει R δύο άνισες πραγματικές ρίζες:
x1=[-(2(1-λ))-2SQRT((λ^2)+1)]/4=[λ-1-SQRT((λ^2)+1)]/2
x2=[-(2(1-λ))+2SQRT((λ^2)+1)]/4=[λ-1+SQRT((λ^2)+1)]/2
Έχουμε
f(x1)=x1(x1+1)=...=[(λ-1-SQRT((λ^2)+1))(λ+1-SQRT((λ^2)+1))]/4
f(x2)=x2(x2+1)=...=[(λ-1+SQRT((λ^2)+1))(λ+1+SQRT((λ^2)+1))]/4
f΄(x1)=2x1+1=...=λ-SQRT((λ^2)+1)
f΄(x2)=2x2+1=...=λ+SQRT((λ^2)+1)
Τα σημεία τομής της (ζ) με την Cf είναι τα Α(x1,f(x1)), Β(x2,f(x2)) και οι εφαπτομένες (ε1) και (ε2) της Cf στα Α και Β έχουν συντελεστή διεύθυνσης λ1=f΄(x1)=λ-SQRT((λ^2)+1) και λ2=f΄(x2)=λ-+QRT((λ^2)+1) αντίστοιχα.
Παρατηρούμε ότι
λ1λ2=[λ-SQRT((λ^2)+1)][λ+SQRT((λ^2)+1)]=(λ^2)-((λ^2)+1)=-1
Άρα λ1λ2=-1 για κάθε λ ανήκει R, που σημαίνει ότι οι (ε1) και (ε2) είναι κάθετες
(γ) Οι εξισώσεις των (ε1) και (ε2) είναι οι εξής:
(ε1): y-f(x1)=f΄(x1)(x-x1) <=> y=f΄(x1)x+f(x1)-x1f΄(x1) <=>
<=> y=[λ-SQRT((λ^2)+1)]x+{[(λ-1-SQRT((λ^2)+1))(λ+1-SQRT((λ^2)+1))]/4}-[{λ-1-SQRT((λ^2)+1)]/2}[λ-SQRT((λ^2)+1)] <=>
<=> y=[λ-SQRT((λ^2)+1)]x-{[(λ-1-SQRT((λ^2)+1))^2]/4}
(ε2): y-f(x2)=f΄(x2)(x-x2) <=> y=f΄(x2)x+f(x2)-x2f΄(x2) <=>
<=> y=[λ+SQRT((λ^2)+1)]x+{[(λ-1+SQRT((λ^2)+1))(λ+1+SQRT((λ^2)+1))]/4}-[{λ-1+SQRT((λ^2)+1)]/2}[λ+SQRT((λ^2)+1)] <=>
<=> y=[λ+SQRT((λ^2)+1)]x-{[(λ-1+SQRT((λ^2)+1))^2]/4}
Οι συντεταγμένες του σημείου τομής Γ(x0,y0) των (ε1) και (ε2) (οι οποίες τέμνονται εφόσον είναι κάθετες) ικανοποιεί τις εξισώσεις και των δύο ευθειών:
y0=[λ-SQRT((λ^2)+1)]x0-{[(λ-1-SQRT((λ^2)+1))^2]/4} (1)
y0=[λ+SQRT((λ^2)+1)]x0-{[(λ-1+SQRT((λ^2)+1))^2]/4} (2)
Εξισώνοντας τα μέλη των εξισώσεων (1) και (2) προκύπτει:
[λ-SQRT((λ^2)+1)]x0-{[(λ-1-SQRT((λ^2)+1))^2]/4} =[λ+SQRT((λ^2)+1)]x0-{[(λ-1+SQRT((λ^2)+1))^2]/4}
................
2SQRT((λ^2)+1)x0=(λ-1)SQRT((λ^2)+1) <=> x0=(λ-1)/2
Αντικαθιστώντας την x0=(λ-1)/2 είτε στην (1) είτε στην (2) προκύπτει και μετά την εκτέλεση των πράξεων προκύπτει ότι y0=-1/2 για κάθε λ ανήκει R.
Άρα το σημείο Μ((λ-1)/2,-1/2) κινείται στην ευθεία y=-1/2 για κάθε λ ανήκει R.



 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki





