Βοήθεια/Aπορίες στα Μαθηματικά Προσανατολισμού

P@NT?LO$ · 15-01-13

Αρχική Δημοσίευση από styt_geia:
Το μόνο που μπορώ να σκεφτώ είναι να πας να βρεις διαστήματα μονοτονίας κλπ για να δείξεις ότι έχει ακριβώς δύο ρίζες, όμως τα νούμερα δεν βολεύουν. Ίσως κάποιος έχει κάποια καλλίτερη ιδέα.

ετσι πηγα εγω να το κανω αλλα δεν βολευουν οπως λες κι εσυ τα νουμερα... στηνπαραγωγισιμη δεν μπορω ναβρω λυσεις!! :worry:

Χαρουλιτα · 15-01-13

Μπορει καποιος να υπολογισει το ολοκληρωμα του συν^2(χ)?
Εχω κολλησει ασχημα!

lowbaper92 · 15-01-13

Αρχική Δημοσίευση από Χαρουλιτα:
Μπορει καποιος να υπολογισει το ολοκληρωμα του συν^2(χ)?
Εχω κολλησει ασχημα!

${cos}^{2}x=\frac{1+cos2x}{2}$

$\int cos2x\, dx=\frac{1}{2}sin2x+c$

Civilara · 15-01-13

Αρχική Δημοσίευση από Χαρουλιτα:
Μπορει καποιος να υπολογισει το ολοκληρωμα του συν^2(χ)?
Εχω κολλησει ασχημα!

$\int {cos}^{2}xdx=\int \frac{1+cos2x}{2}dx=\frac{1}{2}\int 1dx+\frac{1}{4}\int 2cos2xdx=\frac{1}{2}x+\frac{1}{4}sin2x+c=\frac{2x+sin2x}{4}+c=\frac{x+sinxcosx}{2}+c$

όπου

cosx=συνx
sinx=ημx

Χαρουλιτα · 15-01-13

Αντε μωρε, εμεις δεν εχουμε κανει τριγωνομετρικα, γι' αυτο δεν μου εβγαινε...
Και ενα ακομα: Ολοκληρωμα 1/(χ^2-1)^2 dx

Civilara · 15-01-13

Αρχική Δημοσίευση από Χαρουλιτα:
Αντε μωρε, εμεις δεν εχουμε κανει τριγωνομετρικα, γι' αυτο δεν μου εβγαινε...
Και ενα ακομα: Ολοκληρωμα 1/(χ^2-1)^2 dx

Θεωρούμε την συνάρτηση f με τύπο f(x)=1/[((x^2)-1)^2] με πεδίο ορισμού Α=(-00,-1)U(-1,1)U(1,+oo). Η f είναι συνεχής στο Α ως ρητή, επομένως είναι ολοκληρώσιμη σε κάθε διάστημα Δ που είναι υποσύνολο του Α. Για κάθε x ανήκει Α έχουμε:

f(x)=1/[((x^2)-1)^2]=1/[((x-1)(x+1))^2]=1/[((x-1)^2)((x+1)^2)]

Στη συνέχεια θα προσδιοριστούν οι πραγματικοί αριθμοί Α, Β, Γ, Δ έτσι ώστε για κάθε x ανήκει Α να ισχύει:
f(x)=[A/(x-1)]+[B/((x-1)^2)]+[Γ/(x+1)]+[Δ/((x+1)^2)]

Έχουμε για κάθε x ανήκει Α:

[A/(x-1)]+[B/((x-1)^2)]+[Γ/(x+1)]+[Δ/((x+1)^2)]=1/[((x-1)^2)((x+1)^2)
A((x+1)^2)(x-1)+B((x+1)^2)+Γ((x-1)^2)(x+1)+Δ((x-1)^2)=1
........
(Α+Γ)(x^3)+(Α+Β-Γ+Δ)(x^2)+(-Α+2Β-Γ-2Δ)x+(-Α+Β+Γ+Δ-1)=0 για κάθε x ανήκει Α

Επομένως πρέπει να ισχύουν οι σχέσεις:

Α+Γ=0 (1)
Α+Β-Γ+Δ=0 (2)
-Α+2Β-Γ-2Δ=0 (3)
-Α+Β+Γ+Δ-1=0 (4)

Από την επίλυση του παραπάνω συστήματος βρίσκουμε ότι Α=-1/4 και Β=Γ=Δ=1/4. Συνεπώς:

f(x)=1/[((x^2)-1)^2]=1/[((x-1)^2)((x+1)^2)]=-(1/4)[1/(x-1)]+(1/4)[1/((x-1)^2)]+(1/4)[1/(x+1)]+(1/4)[1/((x+1)^2)]

Λαμβάνοντας υπόψη τα ολοκληρώματα:

$\int \frac{1}{x-\alpha }dx=\int \frac{(x-\alpha )'}{(x-\alpha) }dx=\int \left(ln|x-\alpha | \right)'dx=ln|x-\alpha |+c$
$\int \frac{1}{{(x-\alpha )}^{2}}dx=-\int \left(\frac{1}{x-\alpha } \right)'dx=-\frac{1}{x-\alpha }+c$

Έχουμε

$\int f(x)dx=-\frac{1}{4}ln|x-1|-\frac{1}{4(x-1)}+\frac{1}{4}ln|x+1|-\frac{1}{4(x+1)}+c=\frac{1}{4}ln\left|\frac{x+1}{x-1} \right|-\frac{x}{2\left({x}^{2}-1 \right)}+c$

φρι · 16-01-13

αν θελω να χρησιμοποιησω τη μονοτονια της αντιστροφης πρεπει αποδειξη;

Civilara · 16-01-13

Αρχική Δημοσίευση από φρι:
αν θελω να χρησιμοποιησω τη μονοτονια της αντιστροφης πρεπει αποδειξη;

Ναι. Η απόδειξη είναι απλή και την έχω παραθέσει κάπου εδώ μέσα.

Civilara · 16-01-13

Αρχική Δημοσίευση από JKaradakov:
Έχω την παρακάτω άσκηση την οποία έλυσα απλώς θέλω να τσεκάρω λύσεις. Το β,γ αναλυτικά παρακαλώ
Μια συνάρτηση $f:R\rightarrow R$ έχει την ιδιότητα: $f(x-2)\leq x^2-3x+2\leq f(x-3)+2x-4$
Έστω μεταβλητή ευθεία η οποία διέρχεται απο το σημείο $M(-\frac{1}{2},0)$ και τέμνει τη $C_f$ σε δύο διαφορετικά σημεία Α και Β.
α) Να βρεθεί ο τύπος της f
β) Να αποδειχθεί ότι οι εφαπτόμενες της $C_f$ στα Α,Β τέμνονται κάθετα.
γ) Να αποδειχθεί ότι το σημείο τομής των παραπάνω εφαπτομένων κινείται στην σταθερή ευθεία με εξίσωση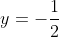 $y=-\frac{1}{2}$

(α) Για κάθε x ανήκει R ισχύει f(x-2)<=(x^2)-3x+2. Επομένως έχουμε:
f((x+2)-2)<=((x+2)^2)-3(x+2)+2 <=> f(x)<=(x^2)+4x+4-3x-6+2 <=> f(x)<=(x^2)+x, x ανήκει R

Για κάθε x ανήκει R ισχύει f(x-3)+2x-4>=(x^2)-3x+2 <=> f(x-3)>=(x^2)-5x+6. Επομένως έχουμε:

f((x+3)-3)>=((x+3)^2)-5(x+3)+6 <=> f(x)>=(x^2)+6x+9-5x-15+6 <=> f(x)>=(x^2)+x, x ανήκει R

Επειδή (x^2)+x<=f(x)<=(x^2)+x για κάθε x ανήκει R τότε f(x)=(x^2)+x=x(x+1) για κάθε x ανήκει R.

Η συνάρτηση f είναι συνεχής και παραγωγίσιμη στο R ως πολυωνυμική με πρώτη παράγωγο f΄(x)=2x+1.

(β) Εφόσον η ευθεία (ζ) τέμνει την Cf σε δύο διαφορετικά σημεία A(x1,f(x1)), B(x2,f(x2)) με x1<x2 τότε η ευθεία (ζ) δεν είναι κατακόρυφη. Επομένως αν η ευθεία (ζ) έχει συντελεστή διεύθυνσης λ και διέρχεται από το σημείο (0,β) τότε έχει εξίσωση της μορφής:

(ζ): y=λx+β

Η (ζ) διέρχεται από το Μ(-1/2,0) οπότε έχουμε:
0=λ*(-1/2)+β <=> β=λ/2

Επομένως η εξίσωση της (ζ) έχει τη μορφή:

(ζ): y=λx+λ/2 <=> y=λ(x+(1/2)), λ ανήκει R

Για να βρούμε τα σημεία τομής της Cf με την (ζ) λύνουμε την εξίσωση y=f(x) όπου y=λ(x+(1/2)). Έχουμε:

f(x)=λ(x+(1/2)) <=> (x^2)+x=λx+(λ/2) <=> (x^2)+(1-λ)x-(λ/2)=0 <=> 2(x^2)+2(1-λ)x-λ=0

Η διακρίνουσα της παραπάνω εξίσωσης είναι:
Δ=[(2(1-λ))^2]-4*2*(-λ)=4((λ^2)+1)>0 για κάθε λ ανήκει R => SQRT(Δ)=2SQRT((λ^2)+1)

Άρα η εξίσωση f(x)=y έχει για κάθε λ ανήκει R δύο άνισες πραγματικές ρίζες:

x1=[-(2(1-λ))-2SQRT((λ^2)+1)]/4=[λ-1-SQRT((λ^2)+1)]/2
x2=[-(2(1-λ))+2SQRT((λ^2)+1)]/4=[λ-1+SQRT((λ^2)+1)]/2

Έχουμε

f(x1)=x1(x1+1)=...=[(λ-1-SQRT((λ^2)+1))(λ+1-SQRT((λ^2)+1))]/4
f(x2)=x2(x2+1)=...=[(λ-1+SQRT((λ^2)+1))(λ+1+SQRT((λ^2)+1))]/4

f΄(x1)=2x1+1=...=λ-SQRT((λ^2)+1)
f΄(x2)=2x2+1=...=λ+SQRT((λ^2)+1)

Τα σημεία τομής της (ζ) με την Cf είναι τα Α(x1,f(x1)), Β(x2,f(x2)) και οι εφαπτομένες (ε1) και (ε2) της Cf στα Α και Β έχουν συντελεστή διεύθυνσης λ1=f΄(x1)=λ-SQRT((λ^2)+1) και λ2=f΄(x2)=λ-+QRT((λ^2)+1) αντίστοιχα.

Παρατηρούμε ότι

λ1λ2=[λ-SQRT((λ^2)+1)][λ+SQRT((λ^2)+1)]=(λ^2)-((λ^2)+1)=-1
Άρα λ1λ2=-1 για κάθε λ ανήκει R, που σημαίνει ότι οι (ε1) και (ε2) είναι κάθετες

(γ) Οι εξισώσεις των (ε1) και (ε2) είναι οι εξής:

(ε1): y-f(x1)=f΄(x1)(x-x1) <=> y=f΄(x1)x+f(x1)-x1f΄(x1) <=>
<=> y=[λ-SQRT((λ^2)+1)]x+{[(λ-1-SQRT((λ^2)+1))(λ+1-SQRT((λ^2)+1))]/4}-[{λ-1-SQRT((λ^2)+1)]/2}[λ-SQRT((λ^2)+1)] <=>
<=> y=[λ-SQRT((λ^2)+1)]x-{[(λ-1-SQRT((λ^2)+1))^2]/4}

(ε2): y-f(x2)=f΄(x2)(x-x2) <=> y=f΄(x2)x+f(x2)-x2f΄(x2) <=>
<=> y=[λ+SQRT((λ^2)+1)]x+{[(λ-1+SQRT((λ^2)+1))(λ+1+SQRT((λ^2)+1))]/4}-[{λ-1+SQRT((λ^2)+1)]/2}[λ+SQRT((λ^2)+1)] <=>
<=> y=[λ+SQRT((λ^2)+1)]x-{[(λ-1+SQRT((λ^2)+1))^2]/4}

Οι συντεταγμένες του σημείου τομής Γ(x0,y0) των (ε1) και (ε2) (οι οποίες τέμνονται εφόσον είναι κάθετες) ικανοποιεί τις εξισώσεις και των δύο ευθειών:

y0=[λ-SQRT((λ^2)+1)]x0-{[(λ-1-SQRT((λ^2)+1))^2]/4} (1)
y0=[λ+SQRT((λ^2)+1)]x0-{[(λ-1+SQRT((λ^2)+1))^2]/4} (2)

Εξισώνοντας τα μέλη των εξισώσεων (1) και (2) προκύπτει:

[λ-SQRT((λ^2)+1)]x0-{[(λ-1-SQRT((λ^2)+1))^2]/4} =[λ+SQRT((λ^2)+1)]x0-{[(λ-1+SQRT((λ^2)+1))^2]/4}
................
2SQRT((λ^2)+1)x0=(λ-1)SQRT((λ^2)+1) <=> x0=(λ-1)/2

Αντικαθιστώντας την x0=(λ-1)/2 είτε στην (1) είτε στην (2) προκύπτει και μετά την εκτέλεση των πράξεων προκύπτει ότι y0=-1/2 για κάθε λ ανήκει R.

Άρα το σημείο Μ((λ-1)/2,-1/2) κινείται στην ευθεία y=-1/2 για κάθε λ ανήκει R.

φρι · 16-01-13

Αρχική Δημοσίευση από Civilara:
Ναι. Η απόδειξη είναι απλή και την έχω παραθέσει κάπου εδώ μέσα.

Οκ,θα το ψαξω. Σε ευχαριστωωωω

antonisd95 · 16-01-13

Αρχική Δημοσίευση από φρι:
αν θελω να χρησιμοποιησω τη μονοτονια της αντιστροφης πρεπει αποδειξη;

Υπάρχουν κάποιες ασκήσεις στις οποίες μπορείς να αποφύγεις την μονοτονία της αντίστροφης.
Δες όμως την απόδειξη:

Έστω f:Δ-->R .Έστω ότι η f είναι γνησίως αύξουσα.(ανάλογα την άσκησή σου)

Για κάθε χι,χ2 ε Δ με χ1<χ2 έχω : f(χ1)<f(χ2) παίρνω f^-1 και διακρίνω τις περιπτώσεις: ( την αντίστροφη της f , την συμβολίζω με g με Dg=f(Df) )

i) g(f(x1))<g(f(x2)) -->χ1<χ2
ii) g(f(x1))>g(f(x2)) -->χ1>χ2 άτοπο
iii) g(f(x1))=g(f(x2)) -->X1=X2 άτοπο.

άρα g γνησίως αύξουσα.( ενδέχεται να μου έχει ξεφύγει κανένα σάλιο)

P@NT?LO$ · 17-01-13

Εστω μια συνεχης συναρτηση $f:[0,+\propto )\rightarrow R$ η οποια ειναι παραγωγισιμη στο $(0,+\propto )$ . Αν $f(0)=1$ $f'(x)>1$ και $f''(x)>0$ για καθε $x>0$ να δειξετε οτι $x+1<f(x)<xf'(x) +1$ για καθε $x>0$

HELP PLEASE!! :/:

Civilara · 17-01-13

Αρχική Δημοσίευση από P@NT?LO$:
Εστω μια συνεχης συναρτηση $f:[0,+\propto )\rightarrow R$ η οποια ειναι παραγωγισιμη στο $(0,+\propto )$ . Αν $f(0)=1$ $f'(x)>1$ και $f''(x)>0$ για καθε $x>0$ να δειξετε οτι $x+1<f(x)<xf'(x) +1$ για καθε $x>0$

HELP PLEASE!!

Έχει λυθεί στο μήνυμα #6143

P@NT?LO$ · 17-01-13

ευχαριστω πολυ φιλε!!!

mary-blackrose · 18-01-13

καλησπερα!Θα ηθελα τη βοηθεια σας στα παρακατω ολοκληρωματα.....υπαρχει καποια μεθοδολογια που μπορω να ακολουθησω στα ολοκληρωματα με πολυωνυμα..??? :hmm:

$i)\int { \frac { x+1 }{ { x }^{ 2 }-4x+3 } } dx\\ ii)\int { \frac { 1 }{ { x }^{ 3 }-{ 3x }^{ 2 }+2x } } dx\\ iii)\int { \frac { { x }^{ 3 } }{ x-1 } } dx\\ iv)\int { \frac { x }{ { x }^{ 2 }-1 } } dx$

aris-bas · 18-01-13

Αρχική Δημοσίευση από mary-blackrose:
καλησπερα!Θα ηθελα τη βοηθεια σας στα παρακατω ολοκληρωματα.....υπαρχει καποια μεθοδολογια που μπορω να ακολουθησω στα ολοκληρωματα με πολυωνυμα..???

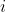$i)\int { \frac { x+1 }{ { x }^{ 2 }-4x+3 } } dx\\ ii)\int { \frac { 1 }{ { x }^{ 3 }-{ 3x }^{ 2 }+2x } } dx\\ iii)\int { \frac { { x }^{ 3 } }{ x-1 } } dx\\ iv)\int { \frac { x }{ { x }^{ 2 }-1 } } dx$

με αφορμη το ποστ της κοπελας θα ηθελα να ρωτησω και γω με τη σειρα μου τι κανουμε στην περιπτωση που ο βαθμος του αριθμητη ειναι μεγαλυτερος απο του παρονομαστη..??
$1)\int { \frac { { x }^{ 3 } }{ x-1 } dx\\ } \\ 2)\int { \frac { { x }^{ 3 }+x+2 }{ { x }^{ 2 }-4 } } dx$

Civilara · 18-01-13

Αρχική Δημοσίευση από mary-blackrose:
$i)\int { \frac { x+1 }{ { x }^{ 2 }-4x+3 } } dx\\$

i) Θεωρούμε το πολυώνυμο P(x)=(x^2)-4x+3, x ανήκει R. Επειδή P(1)=P(3)=0 τότε P(x)=(x-1)(x-3).
Θεωρούμε την συνάρτηση f(x)=(x+1)/((x^2)-4x+3)=(x+1)/P(x)=(x+1)/[(x-1)(x-3)] με πεδίο ορισμού Α=(-οο,1)U(1,3)U(3,+oo). Η f είναι συνεχής στο Α ως ρητή. Συνεπώς είναι ολοκληρώσιμη σε κάθε κλειστό διάστημα Δ υποσύνολο του Α.

Αναζητούμε πραγματικούς αριθμούς Α, Β ώστε για κάθε x ανήκει Α να ισχύει:
f(x)=[A/(x-1)]+[B/(x-3)] <=> (x+1)/[(x-1)(x-3)]=[A/(x-1)]+[B/(x-3)] <=> A(x-3)+B(x-1)=x+1 <=> (A+B)x+(-3A-B)=x+1

Επομένως πρέπει να ισχύουν οι σχέσεις:
A+B=1 <=> B=1-A
-3A-B=1 <=> B=-1-3A
Άρα 1-A=-1-3A <=> 2A=-2 <=> A=-1 και επομένως B=2

Συνεπώς
f(x)=-[1/(x-1)]+[2/(x-3)] για κάθε x ανήκει Α
Επομένως στο διάστημα Δ έχουμε:

$\int f(x)dx=-\int \frac{1}{x-1}dx+2\int \frac{1}{x-3}dx=-ln|x-1|+2ln|x-3|+c$

Civilara · 19 Ιανουαρίου 2013

Αρχική Δημοσίευση από mary-blackrose:
$ii)\int { \frac { 1 }{ { x }^{ 3 }-{ 3x }^{ 2 }+2x } } dx\\$

ii) Θεωρούμε το πολυώνυμο P(x)=(x^2)-3x+2, x ανήκει R. Επειδή P(1)=P(2)=0 τότε P(x)=(x-1)(x-2).
Θεωρούμε το πολυώνυμο Q(x)=xP(x)=x[(x^2)-3x+2]=(x^3)-3(x^2)+2x, x ανήκει R το οποίο γράφεται ισοδύναμα Q(x)=x(x-1)(x-2), x ανήκει R.

Θεωρούμε την συνάρτηση f(x)=1/Q(x)=1/[(x^3)-3(x^2)+2x]=1/[x(x-1)(x-2)] με πεδίο ορισμού A=(-oo,0)U(0,1)U(1,2)U(2,+oo). Η f είναι συνεχής στο Α ως ρητή και επομένως είναι ολοκληρώσιμη σε κάθε κλειστό διάστημα Δ υποσύνολο του Α.

Αναζητούμε πραγματικούς αριθμούς Α, Β, Γ ώστε για κάθε x ανήκει A να ισχύει:

f(x)=(A/x)+[B/(x-1)]+[Γ/(x-2)] <=> 1/[x(x-1)(x-2)]=(A/x)+[B/(x-1)]+[Γ/(x-2)] <=> A(x-1)(x-2)+Bx(x-2)+Γx(x-1)=1 <=>
<=> (A+B+Γ)(x^2)+(-3A-2B-Γ)x+2Α=1

Επομένως πρέπει να ισχύουν οι σχέσεις:
Α+Β+Γ=0 (1)
-3Α-2Β-Γ=0 (2)
2Α=1 (3)

Από την (3) έχουμε Α=1/2 και αν αντικαταστήσουμε στις (1) και (2) προκύπτουν οι εξής σχέσεις:

Β+Γ=-1/2 <=> Γ=-Β-(1/2) (4)
2Β+Γ=-3/2 <=> Γ=-2Β-(3/2) (5)

Από τις (4) και (5) προκύπτει
-Β-(1/2)=-2Β-(3/2) <=> Β=-1, επομένως Γ=1/2

Άρα
f(x)=[1/(2x)]-[1/(x-1)]+[1/(2(x-2))] για κάθε x ανήκει A
Ολοκληρώνοντας την f στο διάστημα Δ έχουμε:

$\int f(x)dx=\frac{1}{2}\int \frac{1}{x}dx-\int \frac{1}{x-1}dx+\frac{1}{2}\int \frac{1}{x-2}dx=\frac{1}{2}ln|x|-ln|x-1|+\frac{1}{2}ln|x-2|+c$

Civilara · 18-01-13

Αρχική Δημοσίευση από mary-blackrose:
$iii)\int { \frac { { x }^{ 3 } }{ x-1 } } dx\\$

iii) Θεωρούμε την συνάρτηση f(x)=(x^3)/(x-1) με πεδίο ορισμού το Α=(-οο,1)U(1,+οο). Η f είναι συνεχής στο Α ως ρητή και συνεπώς είναι ολοκληρώσιμη σε κάθε κλειστό διάστημα Δ υποσύνολο του Α. Για κάθε x ανήκει Α έχουμε:

f(x)=(x^3)/(x-1)=[(x^3)-1+1]/(x-1)={[(x^3)-1]/(x-1)}+[1/(x-1)]={[(x-1)[(x^2)+x+1)]/(x-1)}+[1/(x-1)]=(x^2)+x+1+[1/(x-1)]

Ολοκληρώνοντας την f στο Δ έχουμε:

$\int f(x)dx=\int {x}^{2}dx+\int xdx+\int 1dx+\int \frac{1}{x-1}dx=\frac{{x}^{3}}{3}+\frac{{x}^{2}}{2}+x+ln|x-1|+c$

Civilara · 18-01-13

Αρχική Δημοσίευση από mary-blackrose:
$iv)\int { \frac { x }{ { x }^{ 2 }-1 } } dx$

Θεωρούμε την συνάρτηση f(x)=x/[(x^2)-4]=x/[(x-2)(x+2)] με πεδίο ορισμού το A=(-oo,-2)U(-2,2)U(2,+oo). Η f είναι συνεχής στο Α ως ρητή και επομένως είναι ολοκληρώσιμη σε κάθε κλειστό διάστημα Δ υποσύνολο του Α.

Ολοκληρώνοντας την f στο Δ έχουμε:

$\int f(x)dx=\int \frac{x}{{x}^{2}-4}dx=\frac{1}{2}\int \frac{2x}{{x}^{2}-4}dx=\frac{1}{2}\int \frac{\left( {x}^{2}-4\right)'}{{x}^{2}-4}dx=\frac{1}{2}ln\left|{x}^{2}-4 \right|+c$

Βοήθεια/Aπορίες στα Μαθηματικά Προσανατολισμού

Νεοφερμένος

Διάσημο μέλος

Πολύ δραστήριο μέλος

Περιβόητο μέλος

Διάσημο μέλος

Περιβόητο μέλος

Διάσημο μέλος

Περιβόητο μέλος

Περιβόητο μέλος

Διάσημο μέλος

Δραστήριο μέλος

Νεοφερμένος

Περιβόητο μέλος

Νεοφερμένος

Εκκολαπτόμενο μέλος

Νεοφερμένος

Περιβόητο μέλος

Περιβόητο μέλος

Περιβόητο μέλος

Περιβόητο μέλος