

γινεται;;
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


απλά το έγραψα κατευθείαν και μάλλον μπερδεύτηκες.
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


Αν έχειςκαι
τότε δεν ισχύει ότι
; Έτσι λοιπόν κι εδώ είναι
απλά το έγραψα κατευθείαν και μάλλον μπερδεύτηκες.
αναμεσα δε μπαινει διπλη συνεπαγωγη <=>?
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


αα...
αλλο ενα πραγμα που μπερδευομαι!με την ισοδυναμια και την συνεπαγωγη :\
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος



Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


Αν είναι μεγάλες οι παραστάσεις προτιμώ κατακόρυφα. Αλλιώς οριζόντια. Είναι καθαρά θέμα καλαισθησίας και κανείς δεν θα σε κατηγορήσει γιαυτό. Η αλήθεια βέβαια είναι ότι ένα ευπαρουσίαστο γραπτό προδιαθέτει ευχάριστα
ναι,εχεις δικιο..σε ευχαριστω για ολα!
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
antonisd95
Δραστήριο μέλος


Άρα με τριγωνική βγαίνει.Τι μου ελεγαν οτι δεν μπορώ να αξιοποιήσω την τριγωνική .
Η ολοκληρωμένη εκφώνηση είναι :
Δίνεται συνάρτησημε

για την οποία ισχύει : οριο της g(x) όταν το χ τείνει στο +απειρο ειναι ισο με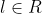
α) Να βρείτε το
β) Γιανα αποδείξετε οτι
=\frac{1+\frac{1}{x}}{\sqrt{1+\frac{1}{x}+\frac{1}{{x}^{2}}}+1} +\beta)
και επίσης οτι.
Δίνονται επίσης οι μιγαδικοίκαι η συνάρτηση :
για την οποία ισχύουν :
οριο της f(x) όταν το χ τείνει στο +απειρο ειναι ίσο μεκαι
.
α)Να αποδείξετε οτι ο γτ της εικονας του ειναι ο κύκλος με κέντρο το σημείο Kκαι ακτίνα
.
β)Να βρείτε το γτ της εικόνας του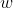
γ)Να αποδείξετε οτι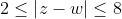
δ) Να αποδείξετε οτι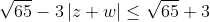
Την άσκηση την έλυσα ολη εκτος απο το δ που ρώτησα ,αν και το ειχα λυσει στο προχειρο με ανισοτητα .Απλα ανεβασα ολο το θεμα για να δειτε αν χρειαζεται κατι για το ερωτημα που ρωτησα,αν και δε νομιζω .
Κάπου είχα διαβάσει οτι απαιτούνται κάποιες προυποθέσεις ωστε να χρησιμοποιήσει κανεις τριγωνικη ανισοτητα στους μιγαδικούς.Ισχύει κάτι τέτοιο ή μπορώ να λυσω το ερωτημα χωρις να γραψω τιποτα παραπάνω;
Σε τι βιβλία υπάρχουν αυτές οι ασκήσεις;...ρωτάω γιατί λύνω ασκήσεις από παπαδάκη,μπάρλα και που και που από στεργίου, αλλά δεν είμαι ικανοποιημένος με το επίπεδο.(όχι ότι αυτή είναι δύσκολη, απλά είναι μεγάλη)
Επίσης θα μπορούσε κάποιος να με παραπέμψει σε παρόμοια θέματα με μιγαδικούς που έχουν γραφεί στο φόρουμ;(π.χ. τέτοια που δημιουργούμε εμείς την ανισότητα ή ασκήσεις που τις λύνουμε με γεωμετρικό τρόπο)
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Aris90
Εκκολαπτόμενο μέλος


για καθε χεR και
i)να αποδειξετε οτι ηf(x) διατηρει προσημο το οποιο και να βρειτε
ii)να βρειτε την τιμη f(o)
σας παρακαλω θελω βοηθεια σε αυτη την ασκηση και αν γινεται θα ηθελα αναλυτικα καθε βημα που πρεπει να κανουμε
ευχαριστω εκ των προτερων
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


εστω συνεχης συναρτησητετοια ωστε να ισχυει :
για καθε χεR και
i)να αποδειξετε οτι ηf(x) διατηρει προσημο το οποιο και να βρειτε
ii)να βρειτε την τιμη f(o)
σας παρακαλω θελω βοηθεια σε αυτη την ασκηση και αν γινεται θα ηθελα αναλυτικα καθε βημα που πρεπει να κανουμε
ευχαριστω εκ των προτερων
Από την αρχική σχέση έχουμε:
(f(x)^2)-2f(x)ημx=((ημx)^4)+((ημx)^2)+1
(f(x)^2)-2f(x)ημx+((ημx)^2)=((ημx)^4)+2((ημx)^2)+1
(f(x)-ημx)^2=(((ημx)^2)+1)^2
[(f(x)-ημx)^2]-[(((ημx)^2)+1)^2]=0
[f(x)-ημx+((ημx)^2)+1][f(x)-ημx-((ημx)^2)-1]=0
[f(x)+((ημx)^2)-ημx+1][f(x)-((ημx)^2)-ημx-1]=0
Η τελευταία σχέση γράφεται στη μορφή [f(x)-g(x)][f(x)-h(x)]=0 για κάθε x ανήκει R όπου
g(x)=-((ημx)^2)+ημx-1
h(x)=((ημx)^2)+ημx+1
x ανήκει R
Άρα για κάθε x ανήκει R ισχύει f(x)=g(x) ή f(x)=h(x) και επειδή η f είναι συνάρτηση θα ισχύει η μία από τις δύο ισότητες για κάθε x ανήκει R.
Θεωρούμε τα πολυώνυμα:
G(x)=-(x^2)+x-1
H(x)=(x^2)+x+1
Θα προσδιοριστεί το πρόσημο των πολυωνύμων G και H για κάθε x ανήκει R. Γι αυτό υπολογίζονται αρχικά οι διακρίνουσες των εξισώσεων G(x)=0 και H(x)=0. Έχουμε
G(x)=0: Δ1=((-1)^2)-4*(-1)*(-1)=1-4=-3<0 => G(x)<0 για κάθε x ανήκει R
H(x)=0: Δ2=(1^2)-4*1*1=1-4=-3<0 => H(x)>0 για κάθε x ανήκει R
Επειδή g(x)=G(ημx) τότε για κάθε x ανήκει R ισχύει g(x)<0
Επειδή h(x)=H(ημx) τότε για κάθε x ανήκει R ισχύει h(x)>0
Επειδή για κάθε x ανήκει R ισχύει είτε f(x)=g(x)<0 είτε f(x)=h(x)>0 τότε προκύπτει ότι για κάθε x ανήκει R είναι f(x) διάφορο 0. Συνεπώς η f διατηρεί σταθερό πρόσημο στο R αφού είναι συνεχής σε αυτό και ισχύει f(x) διάφορο 0 για κάθε x ανήκει R.
Γνωρίζουμε ότι f(π/2)=3>0. Επομένως f(x)>0 για κάθε x ανήκει R αφού η f διατηρεί σταθερό πρόσημο. Συνεπώς f(x)=h(x) για κάθε x ανήκει R. Έτσι λοιπόν έχει βρεθεί ότι:
f(x)=h(x)=((ημx)^2)+ημx+1, x ανήκει R
Για x=0 προκύπτει f(0)=((ημ0)^2)+ημ0+1=1
Παρατηρούμε ότι επαληθεύεται f(π/2)=((ημ(π/2))^2)+ημ(π/2)+1=3
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Aris90
Εκκολαπτόμενο μέλος


Από την αρχική σχέση έχουμε:
(f(x)^2)-2f(x)ημx=((ημx)^4)+((ημx)^2)+1
(f(x)^2)-2f(x)ημx+((ημx)^2)=((ημx)^4)+2((ημx)^2)+1
(f(x)-ημx)^2=(((ημx)^2)+1)^2
[(f(x)-ημx)^2]-[(((ημx)^2)+1)^2]=0
[f(x)-ημx+((ημx)^2)+1][f(x)-ημx-((ημx)^2)-1]=0
[f(x)+((ημx)^2)-ημx+1][f(x)-((ημx)^2)-ημx-1]=0
Η τελευταία σχέση γράφεται στη μορφή [f(x)-g(x)][f(x)-h(x)]=0 για κάθε x ανήκει R όπου
g(x)=-((ημx)^2)+ημx-1
h(x)=((ημx)^2)+ημx+1
x ανήκει R
Άρα για κάθε x ανήκει R ισχύει f(x)=g(x) ή f(x)=h(x) και επειδή η f είναι συνάρτηση θα ισχύει η μία από τις δύο ισότητες για κάθε x ανήκει R.
Θεωρούμε τα πολυώνυμα:
G(x)=-(x^2)+x-1
H(x)=(x^2)+x+1
Θα προσδιοριστεί το πρόσημο των πολυωνύμων G και H για κάθε x ανήκει R. Γι αυτό υπολογίζονται αρχικά οι διακρίνουσες των εξισώσεων G(x)=0 και H(x)=0. Έχουμε
G(x)=0: Δ1=((-1)^2)-4*(-1)*(-1)=1-4=-3<0 => G(x)<0 για κάθε x ανήκει R
G(x)=0: Δ2=(1^2)-4*1*1=1-4=-3<0 => H(x)>0 για κάθε x ανήκει R
Επειδή g(x)=G(ημx) τότε για κάθε x ανήκει R ισχύει g(x)<0
Επειδή h(x)=H(ημx) τότε για κάθε x ανήκει R ισχύει h(x)>0
Επειδή για κάθε x ανήκει R ισχύει είτε f(x)=g(x)<0 είτε f(x)=h(x)>0 τότε προκύπτει ότι για κάθε x ανήκει R είναι f(x) διάφορο 0. Συνεπώς η f διατηρεί σταθερό πρόσημο στο R αφού είναι συνεχής σε αυτό και ισχύει f(x) διάφορο 0 για κάθε x ανήκει R.
Γνωρίζουμε ότι f(π/2)=3>0. Επομένως f(x)>0 για κάθε x ανήκει R αφού η f διατηρεί σταθερό πρόσημο. Συνεπώς f(x)=h(x) για κάθε x ανήκει R. Έτσι λοιπόν έχει βρεθεί ότι:
f(x)=h(x)=((ημx)^2)+ημx+1, x ανήκει R
Για x=0 προκύπτει f(0)=((ημ0)^2)+ημ0+1=1
Παρατηρούμε ότι επαληθεύεται f(π/2)=((ημ(π/2))^2)+ημ(π/2)+1=3
αρα
αρα συνεχης στo R
η f διατηρει προσημο σταθερο επειδη
ii)απο τη σχεση (f(x)^2)-2f(x)ημx=((ημx)^4)+((ημx)^2)+1 βαζουμε οπου χ=0
και καταληγουμε f²(0)-1=0
(f(0)-1)(f(0)+1)=0
f(0)=1 δεκτο και f(0)=-1 αδυνατο γιατι f(x)>0
σε ευχαριστω για την αμμεση απαντηση σου αλλα εχω παρει και αλλη μια απαντηση και θελω να ρωτησω αν ειναι σωστη και αν ειναι σωστη
εχω καποιες χαζες αποριες λοιπον αν θελω να την εξηγησω σε καποιον
αρχικα θα πουμε οτι το ημ^χ+ημ^2χ+1>0 αυτο ειναι θετικο αρα και το πρωτο μελος θα ειναι θετικο
κανουμε τις πραξεις και καταληγουμε f(χ)<>0 το οτι ειναι διαφορετικο του μηδενος αυτο το συμπερασμα το βγαζουμε επειδη ειναι ειναι θετικο το f(x)?
και γιατι λεμε οτι ειναο συνεχης στο R τι συμπερασμα βγαζουμε?
και τελος για να δικαιολογησουμε οτι διατηρει προσημο θα πουμε επειδη f(χ)>0 και ισχυει f(π/2)=3?
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


αρχικα θα πουμε οτι το ημ^χ+ημ^2χ+1>0 αυτο ειναι θετικο αρα και το πρωτο μελος θα ειναι θετικο
κανουμε τις πραξεις και καταληγουμε f(χ)<>0 το οτι ειναι διαφορετικο του μηδενος αυτο το συμπερασμα το βγαζουμε επειδη ειναι ειναι θετικο το f(x)?
και γιατι λεμε οτι ειναο συνεχης στο R τι συμπερασμα βγαζουμε?
και τελος για να δικαιολογησουμε οτι διατηρει προσημο θα πουμε επειδη f(χ)>0 και ισχυει f(π/2)=3?
Αν μία συνάρτηση F (χρησιμοποιώ άλλο σύμβολο για να μην γίνει σύγχυση με την συνάρτηση f της άσκησης) είναι συνεχής σε ένα διάστημα Δ και ισχύει F(x) διάφορο 0 για κάθε x στο Δ τότε η F διατηρεί σταθερό πρόσημο στο Δ, δηλαδή F(x)<0 για κάθε x ανήκει Δ ή F(x)>0 για κάθε x ανήκει Δ.
Γνωρίζουμε ότι η f είναι συνεχής και βρίσκουμε ότι f(x) διάφορο 0 για κάθε x στο R. Άρα η f διατηρεί σταθερό πρόσημο. Επειδή ξέρουμε ότι f(π/2)=3>0 και επειδή η f διατηρεί σταθερό πρόσημο στο R τότε f(x)>0 για κάθε x στο R.
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Αυτό δεν ισχύει. Θα μπορούσε για παράδειγμα να είναιΆρα για κάθε x ανήκει R ισχύει f(x)=g(x) ή f(x)=h(x) και επειδή η f είναι συνάρτηση θα ισχύει η μία από τις δύο ισότητες για κάθε x ανήκει R.
Άλλωστε αν είχες εξαρχής αυτό το αποτέλεσμα, αυτό σημαίνει ότι θα ήξερες πως η f διατηρεί πρόσημο οπότε με βάση την τιμή
Σωστή είναι η δεύτερη. Γενικά ισχύει το εξής:αρχικα θα πουμε οτι το ημ^χ+ημ^2χ+1>0 αυτο ειναι θετικο αρα και το πρωτο μελος θα ειναι θετικο
κανουμε τις πραξεις και καταληγουμε f(χ)<>0 το οτι ειναι διαφορετικο του μηδενος αυτο το συμπερασμα το βγαζουμε επειδη ειναι ειναι θετικο το f(x)?
Αν
Το υπερανάλυσα για να το χωνέψεις αλλά στην πραγματικότητα εκείνο που αρκεί να πεις είναι ότι εφ' όσον η παράσταση στο δεξί μέλος είναι διάφορη του 0 τότε υποχρεωτικά θα είναι και
Κι εδώ θα προσπαθήσω να είμαι αναλυτικός και ελπίζω να το πετύχω με το παρακάτω παράδειγμα. Ας θεωρήσουμε την συνάρτησηκαι γιατι λεμε οτι ειναο συνεχης στο R τι συμπερασμα βγαζουμε?
Η
Η
Μήπως η
Φαίνεται λίγο περίεργη αλλά και αυτή την κάνει την δουλειά. Ας πάρουμε αυτή την τελευταία να την δούμε λίγο προσεκτικά.
Αυτή η συνάρτηση λοιπόν η τελευταία τι χαρακτηριστικά έχει; Ισχύει για παράδειγμα ότι
Τι άλλο μπορούμε να πούμε για την
Ας προσθέσουμε τώρα στις (*) την επιπλέον υπόθεση της συνέχειας για την g σε όλο το [-1,1] και ας ονομάσουμε τις καινούριες υποθέσεις (**). Τι άλλαξε τώρα; Μπορώ να δεχθώ πλέον την
Το ότι διατηρεί πρόσημο το συμπεραίνειςκαι τελος για να δικαιολογησουμε οτι διατηρει προσημο θα πουμε επειδη f(χ)>0 και ισχυει f(π/2)=3?
α) Επειδή έχεις δείξει ότι
β) Επειδή η f είναι συνεχής στους πραγματικούς.
Μέχρι τώρα λοιπόν ξέρουμε ότι είτε
Για να αποφασίσουμε τι από τα δύο ισχύει τελικά πρέπει οπωσδήποτε να ξέρω την τιμή της f σε ένα οποιοδήποτε σημείο. Το πρόσημο της τιμής αυτής θα είναι προφανώς και το πρόσημο όλων των τιμών της f (αφού είπαμε η f διατηρεί πρόσημο). Εδώ έχουμε
Απορίες;

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


Αυτό δεν ισχύει. Θα μπορούσε για παράδειγμα να είναι
Άλλωστε αν είχες εξαρχής αυτό το αποτέλεσμα, αυτό σημαίνει ότι θα ήξερες πως η f διατηρεί πρόσημο οπότε με βάση την τιμήθα συμπέραινες ότι
και τελειώσαμε. Δεν θα χρειαζόταν δηλαδή ότι γράφεις παρακάτω.
Το ίδιο πράγμα λέμε ρε Κώστα. Για κάθε x ανήκει R θα ισχύει ή f(x)=g(x) ή f(x)=h(x). Δεν μπορεί να ισχύουν και οι 2 σχέσεις για το ίδιο x. Σαφέστατα μπορούν να υπάρχουν εξ αρχής x1 διάφορο x2 με f(x1)=g(x1) και f(x2)=h(x2) αλλά δεν μπορεί να υπάρχει x3 με f(x3)=g(x3) και f(x3)=h(x3) με g(x3) διάφορο h(x3).
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.



Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


και μια ακομα..
z1,z2 E C w=( z1+z2)/(z1-z2)
Nδο,1)|z1+z2|² + |z1-z2|² = 2|z1|² + 2|z2|²
2)ΑΝ w E R ν.δ.ο z1=λz2
θε΄λω το δευτερο ερωτημα..το πρωτο το εχω λυσει.. οποιος μπορει..θενκς
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Aris90
Εκκολαπτόμενο μέλος


χιλια ευχαρστω με βοηθησες παρα πολυΑν μία συνάρτηση F (χρησιμοποιώ άλλο σύμβολο για να μην γίνει σύγχυση με την συνάρτηση f της άσκησης) είναι συνεχής σε ένα διάστημα Δ και ισχύει F(x) διάφορο 0 για κάθε x στο Δ τότε η F διατηρεί σταθερό πρόσημο στο Δ, δηλαδή F(x)<0 για κάθε x ανήκει Δ ή F(x)>0 για κάθε x ανήκει Δ.
Γνωρίζουμε ότι η f είναι συνεχής και βρίσκουμε ότι f(x) διάφορο 0 για κάθε x στο R. Άρα η f διατηρεί σταθερό πρόσημο. Επειδή ξέρουμε ότι f(π/2)=3>0 και επειδή η f διατηρεί σταθερό πρόσημο στο R τότε f(x)>0 για κάθε x στο R.

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Aris90
Εκκολαπτόμενο μέλος


Αυτό δεν ισχύει. Θα μπορούσε για παράδειγμα να είναι
Άλλωστε αν είχες εξαρχής αυτό το αποτέλεσμα, αυτό σημαίνει ότι θα ήξερες πως η f διατηρεί πρόσημο οπότε με βάση την τιμήθα συμπέραινες ότι
και τελειώσαμε. Δεν θα χρειαζόταν δηλαδή ότι γράφεις παρακάτω.
Σωστή είναι η δεύτερη. Γενικά ισχύει το εξής:
Ανμε
τότε ισχύει ότι
. Αυτό συμβαίνει γιατί αν το α ήταν 0 τότε προφανώς και το c θα ήταν 0, οποίο είναι άτοπο. Κατ' αναλογία έχουμε
με
για κάθε
. Αυτό σημαίνει ότι
για κάθε
. Γιατί συμβαίνει αυτό; Γιατί αν υπήρχε
με
τότε αν βάλουμε στην σχέση όπου
το
θα πάρουμε
κάτι το οποίο είναι άτοπο.
Το υπερανάλυσα για να το χωνέψεις αλλά στην πραγματικότητα εκείνο που αρκεί να πεις είναι ότι εφ' όσον η παράσταση στο δεξί μέλος είναι διάφορη του 0 τότε υποχρεωτικά θα είναι καιγια κάθε
. Τα υπόλοιπα τα έχεις απλά στο μυαλό σου σαν εξήγηση.
Κι εδώ θα προσπαθήσω να είμαι αναλυτικός και ελπίζω να το πετύχω με το παρακάτω παράδειγμα. Ας θεωρήσουμε την συνάρτηση(το διάστημα [-1,1] είναι τυχαίο. Θα μπορούσα να πάρω κάποιο άλλο) για την οποία ισχύει ότι
για κάθε
(*). Δεν ξέρω τίποτε άλλο γι'αυτήν πέρα απ' το ότι
αφού
. Ούτε αν είναι συνεχής ούτε τίποτα. Αν σου έλεγα να μου βρεις κάποιες τέτοιες συναρτήσεις που ικανοποιούν τις υποθέσεις (*) ποια θα ήταν η απάντησή σου;
Η; Βεβαίως!
Η; Γιατί όχι;!
Μήπως η
Φαίνεται λίγο περίεργη αλλά και αυτή την κάνει την δουλειά. Ας πάρουμε αυτή την τελευταία να την δούμε λίγο προσεκτικά.

Αυτή η συνάρτηση λοιπόν η τελευταία τι χαρακτηριστικά έχει; Ισχύει για παράδειγμα ότι. Φυσικά! Δεν μηδενίζεται πουθενά, φαίνεται άλλωστε. Διατηρεί πρόσημο στο [-1,1]; ΟΧΙ Για άλλες τιμές είναι θετική για άλλες αρνητική.
Τι άλλο μπορούμε να πούμε για την; Δεν είναι συνεχής σε όλο το διάστημα [-1,1] . Πράγματι η
δεν είναι συνεχής στο 0 αφού
. Αυτές οι τρεις συναρτήσεις λοιπόν όλες ικανοποιούν τις υποθέσεις (*), άρα η απάντηση θα μπορούσε να είναι οποιαδήποτε από αυτές.
Ας προσθέσουμε τώρα στις (*) την επιπλέον υπόθεση της συνέχειας για την g σε όλο το [-1,1] και ας ονομάσουμε τις καινούριες υποθέσεις (**). Τι άλλαξε τώρα; Μπορώ να δεχθώ πλέον τηνσαν υποψήφια συνάρτηση; Φυσικά και όχι, αφού αυτή δεν είναι συνεχής όπως είδαμε. Η g που ψάχνω πλέον είναι συνεχής και διάφορη του 0 στο διάστημα [-1,1]. Άρα λόγω του γνωστού πορίσματος (σελ 192 πρώτο σχόλιο μετά το θεώρημα Βοlzano ) θα διατηρεί πρόσημο στο [-1,1]. Τι σημαίνει αυτό; Θα είναι είτε
οπότε
είτε
οπότε
. Χμ αν είχα μαζί με τις υποθέσεις (**) και μία τιμή για την g για κάποιο
ίσως να μπορούσα τελικά να καταλήξω στον τύπο της g. Πχ αν μου δίνει
μπορώ με σιγουριά να πω ότι
. Άρα λοιπόν και για να απαντήσω επιτέλους στο ερώτημα που έβαλες, η συνέχεια σ'αυτές τις περιπτώσεις είναι καταλυτική. Μου εξασφαλίζει μέσω του πορίσματος του Bolzano ότι μία συνάρτηση με άγνωστο τύπο, που δεν μηδενίζεται πουθενά σε ένα διάστημα και συνεχής, θα βρίσκεται είτε ολόκληρη πάνω από τον άξονα των χ είτε ολόκληρη κάτω απ' αυτόν. Ότι δεν θα σπάει δηλαδή σε ασυνεχή κομμάτια όπως στην περίπτωση της
Το ότι διατηρεί πρόσημο το συμπεραίνεις
α) Επειδή έχεις δείξει ότιγια κάθε χ πραγματικό.
β) Επειδή η f είναι συνεχής στους πραγματικούς.
Μέχρι τώρα λοιπόν ξέρουμε ότι είτεείτε
Για να αποφασίσουμε τι από τα δύο ισχύει τελικά πρέπει οπωσδήποτε να ξέρω την τιμή της f σε ένα οποιοδήποτε σημείο. Το πρόσημο της τιμής αυτής θα είναι προφανώς και το πρόσημο όλων των τιμών της f (αφού είπαμε η f διατηρεί πρόσημο). Εδώ έχουμεάρα υποχρεωτικά
.
Απορίες;
με καλυψες πληρως
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 4 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 227 μέλη διάβασαν αυτό το θέμα:
- hristosdab
- trifasikodiavasma
- haji
- thepigod762
- Mariosm.
- soulatso
- oteletampis
- phleidhs
- Hased Babis
- AggelikiGr
- sir ImPeCaBlE
- veiNqh
- Scandal
- alekos
- Debugging_Demon
- just some guy
- xristosgkm
- ismember
- Apocalypse
- arrow25
- rempelos42
- ggl
- GStef
- QWERTY23
- xrisamikol
- Σωτηρία
- nikoletaz57
- _Aggelos123
- Mariam38
- SlimShady
- strsismos88
- Georgekk
- Lia 2006
- igeorgeoikonomo
- marian
- tsiobieman
- constansn
- Xristosdimitra
- Panagiotis849
- ρενακι 13
- Memetchi
- eukleidhs1821
- Nikkkpat
- Unboxholics
- korlef
- kwstaseL
- Thanos_D
- the purge
- T C
- Giii
- Papachrist
- liaiscool
- Αννα Τσιτα
- globglogabgalab
- Pharmacist01
- thanahss
- abcdefg12345
- nicole1982
- thecrazycretan
- kvstas92
- KingOfPop
- maria301
- papa2g
- stefan
- Κλημεντίνη
- TonyMontanaEse
- Athens2002
- Alexecon1991
- Μάρκος Βασίλης
- Cortes
- το κοριτσι του μαη
- calliope
- ale
- panagiotis G
- Kleanth
- aggelosst9
- BioChemical
- spring day
- nucomer
- Georgia110
- LeoDel
- pink_panther
- Alexandros973
- marsenis
- den antexw allh apotyxia
- KaterinaL
- kiyoshi
- drosos
- Λαμπρινηη
- Bill22
- Chrysablac.
- giorgosp97
- Βλα
- Monster Hunter
- jul25
- xxxtolis
- Stroka
- nicks1999
- totiloz
- Earendil
- mitsakos
- tasost
- lnesb
- ssalex
- Vasilina93
- alan09
- Livaja10
- χημεια4λαιφ
- Viedo
- UncleJ
- Kostakis45
- Infrared
- Zgian
- pepatogourounaki
- hirasawayui
- GeoCommand
- Eleni54
- American Economist
- EiriniS20
- ΘανάσοςG4
- stamoul1s
- Αριάνα123
- uni77
- Libertus
- tasoss
- PanosCh002
- Unseen skygge
- Νικόλας Ραπ.
- cel123
- The Limit Does Not Exist
- don_vito
- suaimhneas
- Αλκης Κ.
- alexrami
- Baggelitsa36
- Νομικάριος13
- spinalgr1990
- d_th
- Adolfo valencia
- Πα.Κ
- Vasilis25
- Johnman97
- Steffie88
- rekcoR
- gwgw_5
- fockos
- Mariahj
- roud
- kostas83
- Cpt.Philips
- Makis45
- Χρησλου
- Panos_02
- Vold
- tymvorixos
- GiorgosAsi
- Neos167
- theodoraooo
- George187
- Άρτεμις Α.
- Μαρία2222
- christos87
- Idontknoww
- jimis2001
- Metamorph
- Γατόπαρδος.
- Johnsk
- mitsos14
- johnsiak
- Elel
- Dreamer_SW
- Γιαννης1987Θεσσ
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

