1) Aν
={3x}^{2}+5)
να αποδειχθει οτι ειναι συνεχης στο R η
=\frac{f(x)-f(xo)}{x-xo},x\neq xo)
= 6xo,x=xo)
Για x, x0 ανήκουν R ισχύει:
f(x)-f(x0)=3(x^2)+5-3(x0^2)-5=3((x^2)-(x0^2))=3(x+x0)(x-X0)
Επομένως για x διάφορο x0 ισχύει:
g(x)=(f(x)-f(x0))/(x-x0)=3(x+x0)(x-x0)/(x-x0)=3(x+x0)
Άρα η g είναι συνεχής στο (-άπειρο,x0)U(x0,+άπειρο) ως πολυωνυμική
Γνωρίζουμε ότι g(x0)=6x0
lim(x->x0)g(x)=lim(x->x0)[3(x+x0)]=3(x0+x0)=3*2x0=6x0=g(x0)
Επομένως η g είναι συνεχής στο x0. Συνεπώς η g είναι συνεχής στο R.
δινεται η συναρτηση
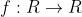
τετοια ωστε για καθε χΕR να ισχυει:
|f(x)-a|<=(x-a)²
ι) να αποδειξεται οτι η f ειναι συνεχης στο xo=α
ιι) να εξετασετε αν ειναι συνεχης στο χο=α η συναρτηση
=\frac{f(x)-a}{x-a},x\neq a)
=f(a),x=a)
ι) |f(x)-a|<=(x-a)^2 <=> -(x-a)^2<=f(x)-a<=(x-a)^2 <=> a-(x-a)^2<=f(x)<=a+(x-a)^2
lim(x->a)[(x-a)^2]=(a-a)^2=0 => lim(x->a)[-(x-a)^2]=-lim[(x-a)^2]=-0=0
Επειδή lim(x->a)[-(x-a)^2]=lim(x->a)[(x-a)^2]=0 τότε σύμφωνα με το κριτήριο παρεμβολής τότε lim(x->a)(f(x)-a)=0 <=> lim(x->a)f(x)=a
Για x=a προκύπτει a-(a-a)^2<=f(a)<=a+(a-a)^2 <=> a<=f(a)<=a <=> f(a)=a
Επομένως lim(x->a)f(x)=f(a). Άρα η f είναι συνεχής στο a
ιι) -(x-a)^2<=f(x)-a<=(x-a)^2
Έχουμε:
lim(x->a)(x-a)=a-a=0 <=> lim(x->a-)(x-a)=lim(x->a+)(x-a)=0
lim(x->a)[-(x-a)]=-(a-a)=0 <=> lim(x->a-)[-(x-a)]=lim(x->a+)[-(x-a)]=0
Αν x<a τότε
x-a<=(f(x)-a)/(x-a)<=-(x-a)
lim(x->a-)(x-a)=lim(x->a-)[-(x-a)]=0 οπότε σύμφωνα με το κριτήριο παρεμβολής lim(x->a-)[(f(x)-a)/(x-a)]=0
Αν x>a τότε
-(x-a)<=(f(x)-a)/(x-a)<=x-a
lim(x->a+)[-(x-a)]=lim(x->a+)(x-a)=0 οπότε σύμφωνα με το κριτήριο παρεμβολής lim(x->a+)[(f(x)-a)/(x-a)]=0
lim(x->a-)[(f(x)-a)/(x-a)]=lim(x->a+)[(f(x)-a)/(x-a)]=0 <=> lim(x->a)[(f(x)-a)/(x-a)]=0
Άρα lim(x->a)g(x)=lim(x->a)[(f(x)-a)/(x-a)]=0. Γνωρίζουμε ότι g(a)=f(a)=a
Αν a=0 τότε g(0)=f(0)=0 και επομένως lim(x->0)g(x)=g(0) που σημαίνει ότι η g είναι συνεχής στο a=0.
Αν a διάφορο 0 τότε g(a)=a διάφορο lim(x->a)g(x)=0 που σημαίνει ότι η g δεν είναι συνεχής στο a για a διάφορο 0.


 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki


 => -3<β-3<0 (αφαιρω και στα δυο μελη το 3)
=> -3<β-3<0 (αφαιρω και στα δυο μελη το 3)


