Βοήθεια/Aπορίες στα Μαθηματικά Προσανατολισμού

[vavlas]

Έστω και .
α)Αν να δειξετε οτι
β)Αν = 5 να βρειτε :
ι)το γεωμετρικο τοπο των εικονων .
ιι)τη μεγιστη τιμη του και την ελαχιστη του .


εχει κανενας καμια ιδεα;;;

Εκμεταλεύσου οτι πάρε δηλαδή οτι f(z)=f(zσυζυγές),αντικατέστησε και θα καταλήξεις σε z=-zσυζυγές

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Θάλεια]

Εκμεταλεύσου οτι πάρε δηλαδή οτι f(z)=f(zσυζυγές),αντικατέστησε και θα καταλήξεις σε z=-zσυζυγές

Μαλιστααα..
Μηπως εχεις + για το 2ο καμια ιδεαα;

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[vavlas]

Μαλιστααα..
Μηπως εχεις + για το 2ο καμια ιδεαα;

Ξέρεις απο την εκφώνηση το άρα ξέρεις και το εξισώνεις το γινόμενο τους με το 5,βάζεις όπου βάζεις χ+yi και καταλήγεις σε ευθεία η σε κάποια κωνική τομή.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[vavlas]

Για να δείξω οτι 2 γραφικές παραστάσεις έχουν μόνο ένα κοινό σημείο,αρκεί να δείξω οτι οι 2 συναρτήσεις f(x) και g(χ) είναι γνησίος μονότονες,και η ισότητα f(x)=g(x) έχει μία προφανής λύση;

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Ricky]

Για να δείξω οτι 2 γραφικές παραστάσεις έχουν μόνο ένα κοινό σημείο,αρκεί να δείξω οτι οι 2 συναρτήσεις f(x) και g(χ) είναι γνησίος μονότονες,και η ισότητα f(x)=g(x) έχει μία προφανής λύση;

Για να δείξεις ότι 2 συναρτήσεις έχουν μόνο ένα κοινό σημείο αρκεί να δείξεις ότι η εξίσωση f(x)=g(x) έχει ακριβώς μία λύση.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[vavlas]

Για να δείξεις ότι 2 συναρτήσεις έχουν μόνο ένα κοινό σημείο αρκεί να δείξεις ότι η εξίσωση f(x)=g(x) έχει ακριβώς μία λύση.

Ναι αλλά αν έχω f(x)=e^(x-1)+ln(x+1) και g(x)=x³+ln2x δεν μπορώ να αποδείξω οτι η f(x)=g(x) οτι έχει μοναδική λύση,απλά μπορώ να δω οτι έχω προφανής ρίζα το χ=1 και να δω αν είναι γνησίος μονότονες για να δω αν είναι μοναδική.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Ricky]

Ναι αλλά αν έχω f(x)=e^(x-1)+ln(x+1) και g(x)=x³+ln2x δεν μπορώ να αποδείξω οτι η f(x)=g(x) οτι έχει μοναδική λύση,απλά μπορώ να δω οτι έχω προφανής ρίζα το χ=1 και να δω αν είναι γνησίος μονότονες για να δω αν είναι μοναδική.

Ναι, πολύ σωστά.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[rebel]

Αν θεωρήσεις την μπορείς να δείξεις κατασκευαστικά ( κτλ) ότι αυτή είναι 1-1 και άρα έχει μοναδική ρίζα;Γιατί με μονοτονία δηλ παραγώγιση και έλεγχο προσήμου λίγο δύσκολο το βλέπω

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[petroskaz]

Δίνονται οι πραγματικοί αριθμοί α,β με β διάφορο του 0 και οι συναρτήσεις f,g:R->R ώστε:
(gog)(x)=ag(x)+bf(x^3+x+2000) για κάθε χ ανήκει στο R
Αν η f είναι 1-1,να αποδείξετε οτι και η g είναι 1-1.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Civilara]

Δίνονται οι πραγματικοί αριθμοί α,β με β διάφορο του 0 και οι συναρτήσεις f,g:R->R ώστε:
(gog)(x)=ag(x)+bf(x^3+x+2000) για κάθε χ ανήκει στο R
Αν η f είναι 1-1,να αποδείξετε οτι και η g είναι 1-1.

Θεωρώ την συνάρτηση h(x)=x³+x+2000. Η h είναι συνεχής και παραγωγίσιμη στο R ως πολυωνυμική με πρώτη παράγωγο h΄(x)=3x²+1. Επειδή h'(x)>0 για κάθε x στο R, τότε η h είναι γνησίως αύξουσα στο R και συνεπώς 1-1.

Η f είναι 1-1, οπότε για κάθε x1,x2 στο R ισχύει f(x1)=f(x2) => χ1=χ2.
Η βασική εξίσωση γράφεται g(g(x))=αg(x)+βf(h(x)), για κάθε x στο R.

Θεωρώ x1, x2 στο R τέτοια ώστε g(x1)=g(x2) => g(x1)-g(x2)=0. Έχουμε:

g(x1)=g(x2) => g(g(x1))=g(g(x2)) => αg(x1)+βf(h(x1))=αg(x2)+βf(h(x2)) => α[g(x1)-g(x2)]=β[f(h(x2))-f(h(x1))] => 0=β[f(h(x2))-f(h(x1))] => f(h(x2))-f(h(x1))=0 => f(h(x1))=f(h(x2))

Επειδή η f είναι 1-1 ισχύει: f(h(x1))=f(h(x2)) => h(x1)=h(x2)
Επειδή η h είναι 1-1 ισχύει: h(x1)=h(x2) => x1=x2

Άρα προκύπτει g(x1)=g(x2) => x1=x2

Συνεπώς η g είναι 1-1.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[akiroskirios]

Ναι αλλά αν έχω f(x)=e^(x-1)+ln(x+1) και g(x)=x³+ln2x δεν μπορώ να αποδείξω οτι η f(x)=g(x) οτι έχει μοναδική λύση,απλά μπορώ να δω οτι έχω προφανής ρίζα το χ=1 και να δω αν είναι γνησίος μονότονες για να δω αν είναι μοναδική.

δεν ισχύει αυτό που λες...αν οι συναρτήσεις είναι γνησίως μονότονες και δεν έχουν την ίδια μονοτονία τότε κάτι γίνεται, απλά δεν έχεις διδαχτεί κάπου ένα τέτοιο θεώρημα...Άρα θέσε συνάρτηση Κ= f - g και δείξε πως έχει μοναδική λύση...

ΥΓ: Βασικά αν αποδείξεις πως η f και η g είναι γνησίως μονότονες και έχουν διαφορετική μονοτονία τότε η -g θα έχει ίδια μονοτονία με την f άρα η f-g θα είναι γνησίως μονότονη και θα έχει τη μονοτονία της f ( x1>x2 κλπ)..Αλλά δεν υπάρχει λόγος να περιπλέκουμε την άσκηση...

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[evangeline]

έχω κολλήσει...
ψάχνω να βρω μια συνάρτηση που να είναι 1-1 αλλά όχι γνησίως μονότονη....

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[vavlas]

δεν ισχύει αυτό που λες...αν οι συναρτήσεις είναι γνησίως μονότονες και δεν έχουν την ίδια μονοτονία τότε κάτι γίνεται, απλά δεν έχεις διδαχτεί κάπου ένα τέτοιο θεώρημα...Άρα θέσε συνάρτηση Κ= f - g και δείξε πως έχει μοναδική λύση...

ΥΓ: Βασικά αν αποδείξεις πως η f και η g είναι γνησίως μονότονες και έχουν διαφορετική μονοτονία τότε η -g θα έχει ίδια μονοτονία με την f άρα η f-g θα είναι γνησίως μονότονη και θα έχει τη μονοτονία της f ( x1>x2 κλπ)..Αλλά δεν υπάρχει λόγος να περιπλέκουμε την άσκηση...

Γενικά 2 γνησίος μονότονες συναρτήσεις μπορούν να έχουν πάνω από ένα σημείο τομής;

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Ricky]

έχω κολλήσει...
ψάχνω να βρω μια συνάρτηση που να είναι 1-1 αλλά όχι γνησίως μονότονη....

Δοκίμασε τη συνάρτηση

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Ricky]

Γενικά 2 γνησίος μονότονες συναρτήσεις μπορούν να έχουν πάνω από ένα σημείο τομής;

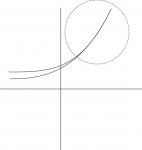
Ναι γίνεται. Για παράδειγμα δες το συνειμμένο που ανέβασα. Έχουμε 2 διαφορετικές συναρτήσεις, γνησίως αύξουσες, που όμως έχουν άπειρα κοινά σημεία (όλα τα σημεία μέσα στον κύκλο).

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[rebel]

f(x)=x, αν χ<1 ή χ>=2
3-χ, αν 1<=χ<2

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Dias]

...συνάρτηση που να είναι 1-1 αλλά όχι γνησίως μονότονη....

Δες στο βιβλίο: σελ. 153 σχήμα (34). Αν δεις αυτό, μετά φτιάχνεις όποια άλλη θέλεις.
Θα σου πω τι μου λένε οι καθηγητές μου: "Πρώτα θα κοιτάς το σχολικό βιβλίο και μετά όλα τα άλλα".

Γενικά 2 γνησίως μονότονες συναρτήσεις μπορούν να έχουν πάνω από ένα σημείο τομής;

Ω, ναι. Δες ένα απλό παράδειγμα: y = x και y = x³

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[vavlas]

Ευχαριστώ πολύ.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[akiroskirios]

Γενικά 2 γνησίος μονότονες συναρτήσεις μπορούν να έχουν πάνω από ένα σημείο τομής;

έντιτ: σε κάλυψε ο Ξένιος

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Ricky]

Ναι αλλά αν έχω f(x)=e^(x-1)+ln(x+1) και g(x)=x³+ln2x δεν μπορώ να αποδείξω οτι η f(x)=g(x) οτι έχει μοναδική λύση,απλά μπορώ να δω οτι έχω προφανής ρίζα το χ=1 και να δω αν είναι γνησίος μονότονες για να δω αν είναι μοναδική.

Μήπως η άσκηση λέει για x>0?

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.