metalmaniac
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
\pi
Νεοφερμένο μέλος


και πώς το ξέρουμε αυτο?
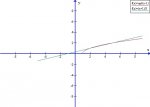
Ένας πρακτικός τρόπος να επαληθεύσεις τη λύση σου είναι να κάνεις τις γραφικές παραστάσεις(δες το συνημμένο).
Ο πιο αλγεβρικός τρόπος είναι να θεωρήσεις τη συνάρτηση h(x)=g(x)-f(x) και να ελέγξεις το πρόσημό της.


Άρα το εμβαδόν που ψάχνεις είναι το άθροισμα του εμβαδού του τριγώνου που σχηματίζεται από την g(x) τον y'y και τις χ=-1,χ=1 και του εμβαδού του χωρίου ανάμεσα στις g(x),f(x), x=1,x=2.
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Συνημμένα
rafaa
Νεοφερμένο μέλος


to be continued...
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


π.ο.f=(0,+oo)δινεται η συναρτηση
to be continued...
Στο π.ο.f η 1/χ και η lnx είναι συνεχείς.
Άρα f συνεχής ως άθροισμα συνεχών.
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
gimli
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lowbaper92
Πολύ δραστήριο μέλος


καλησπερα το ολοκληρωμα lnx/(x+1)^2 dx πως να αρχισω να το υπολογιζω;; ευχαριστω
Οπότε ξεκίνα με παραγοντική.
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
παυλος1
Εκκολαπτόμενο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
forakos
Νεοφερμένο μέλος


g(x)=-xlnx f'(x) και f(x)=-xlnx g'(x)
Aν f(e)=0 και g(e)=-2 να αποδειχθει οτι
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
\pi
Νεοφερμένο μέλος


Η άσκηση που έδωσες έχει ένα μικρό λάθος. Για να ισχύειΓια δυο συναρτησεις f,g: (1,+00)-->R ισχουν:
g(x)=-xlnx f'(x) και f(x)=-xlnx g'(x)
Aν f(e)=0 και g(e)=-2 να αποδειχθει οτικαι
=\frac{1}{lnx}+lnx)
Παρατηρούμε ότι αυτό που θέλουμε ν'αποδείξουμε είναι ότι
Άρα αν προσθέσουμε κατά μέλη τις δύο σχέσεις θα προκύψει
Δουλεύοντας όμοια με αφαίρεση κατά μέλη προκύπτει ότι g(x)-f(x)=2lnx.
Λύνεις το σύστημα και βρίσκεις τους ζητούμενους τύπους.
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
spartgst
Νεοφερμένο μέλος


thnks!Να βαλω μα ακομη πιο δυσκολη τωρα?Δεν εχω λυση παρομοια με αυτη...αν εχετε χρονο βοηθηστε με μια μεθοδολογια!!
ΑΝ Μ1,Μ2 οι εικονες Ζ1,Ζ2 αντιστοιχως και Ζ2=Ζ1+1/Ζ1.Ν.δ.ο¨:οταν το Μ1 κινειται στον κυκλο με κεντρο 0(0.0) και ρ=1.τοτε το Μ2 κινειτα στο ευθυγραμμο τμημα με Α(-2,0),Β(2.0)
Ευχαριστω πρωκαταβολικα!
Ισχύει πως ο z2 είναι πραγματικός |z1|^2=1 άρα z1bar=1/z1
όμως z2=z+1/z=z+zbar
και z2bar=zbar+1/zbar=zbar+z
άρα z2=z2bar οπότε z2 πραγματικός
Ισχύει τώρα ότι |z2|=|z+zbar|
από τριγωνική ανισότητα: |z2|=|z+zbar|<= |z|+|zbar|
άρα |z2|<=2 ,αφού o z2 είναι πραγματικός --> -2<z2<2 άρα o z2 κινείται στην ευθεία A(-2,0)-B(2,0)
Τις μισώ τις αναλύσεις σε x+yi....

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Dias
Επιφανές μέλος


Το ίδιο λέει και ο μαθηματικός μου.Τις μισώ τις αναλύσεις σε x+yi....
 Όμως μερικές φορές δίνουν πιο γρήγορες λύσεις.
Όμως μερικές φορές δίνουν πιο γρήγορες λύσεις. 
 Για να γράφεις πιο καλά δες και πως βγαίνουν σύμβολα κατευθείαν από ελληνικό πληκτρολόγιο:
Για να γράφεις πιο καλά δες και πως βγαίνουν σύμβολα κατευθείαν από ελληνικό πληκτρολόγιο:Δυνάμεις: ² :CTRL+ALT+2, ³ :CTRL+ALT+3, Μοίρες: ° :CTRL+ALT+0, ± : CTRL+ALT+"-",
½ : CTRL+ALT+"+".
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rafaa
Νεοφερμένο μέλος


α) να βρειτε το συνολο τιμων
β) να δειξετε οτι αντιστρεφεται και οτι η f^-1 ειναι γνησιως φθινουσα
γ) να υπολογιστει το lim f(x)-x^2 oπου το lim τεινει στο χ->0+ αν f^-1 ειναι συνεχης.
x+f(x)^-1
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Manthak47
Νεοφερμένο μέλος


Δινεται μια συναρτηση f(x)= 1/x - lnx
α) να βρειτε το συνολο τιμων
β) να δειξετε οτι αντιστρεφεται και οτι η f^-1 ειναι γνησιως φθινουσα
γ) να υπολογιστει το lim f(x)-x^2 oπου το lim τεινει στο χ->0+ αν f^-1 ειναι συνεχης.
x+f(x)^-1
Μπορώ να λύσω μόνο το β:
Αν η συνάρτηση είναι ένα προς ένα, τότε αντιστρέφεται.
Είναι
Με πρόσθεση κατά μέλη των 1 και 2 προκύπτει
Για να είναι γνησίως φθίνουσα:
Από εδώ προκύπτει με πρόσθεση κατά μέλη ότι για κάθε x που ανήκει στο πεδίο ορισμού της f, ισχύει
-------------
εδιτ: Και μόνο να αποδείξουμε ότι είναι γνησίως φθίνουσα φτάνει, επειδή μια μονότονη συνάρτηση είναι 1-1.
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lowbaper92
Πολύ δραστήριο μέλος


Στα υπογραμμισμενα δεν καταλαβαίνω τι ζηταςΔινεται μια συναρτηση f(x)= 1/x - lnx
α) να βρειτε το συνολο τιμων
β) να δειξετε οτι αντιστρεφεται και οτι η f^-1 ειναι γνησιως φθινουσα
γ) να υπολογιστει το lim f(x)-x^2 oπου το lim τεινει στο χ->0+ αν f^-1 ειναι συνεχης.
x+f(x)^-1
α)
Άρα η f γνησίως φθίνουσα.
Όμως
Άρα
Η f γνησίως φθίνουσα και συνεχής άρα
β) Η f ως γνησίως μονότονη είναι και 1-1, άρα αντιστρέφεται.
Η αντίστροφη έχει το ίδιο είδος μονοτονίας με την f.
Απόδειξη: Έστω ότι η αντίστροφη δεν έχει το ίδιο μονοτονίας με την f. Δηλαδή έστω ότι η αντίστροφη είναι γνησίως αύξουσα. Τότε για δύο τυχαία χ1,χ2 του (0,+οο) (έστω χ1<χ2) θα ισχύει
Άρα και η αντίστροφη είναι γνησίως φθίνουσα
γ) Εφόσον ξέρουμε το όριο της f στο 0+ , ξέρουμε και το ζητούμενο.
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
metalmaniac
Νεοφερμένο μέλος


Αν z ανήκει στο c*και ισχυει |((z^3)+1/z)|<=2 να βρείτε τον γεωμετρικό τοπο του όταν |(z+1/z)|=2
An για καθε χ ανηκει R ισχυέι (ολοκλήρωμα απο 0 ως χ)|z|f(t)dt=(e^x)-1.Nα βρείτε τον z όταν f(x)=(e^x)/|z-i|
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rafaa
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
forakos
Νεοφερμένο μέλος


Πως αποδεικνυω οτι f(x)+g(x) διαφορο του μηδενος για να διαιρεσω;Η άσκηση που έδωσες έχει ένα μικρό λάθος. Για να ισχύειθα πρέπει να είναι g(e)=2.
Παρατηρούμε ότι αυτό που θέλουμε ν'αποδείξουμε είναι ότιενώ g(x)-f(x)=2lnx. Δηλαδή από τις σχέσεις που μας δίνουν θέλουμε να προκύψει σύστημα με άθροισμα και διαφορά.
Άρα αν προσθέσουμε κατά μέλη τις δύο σχέσεις θα προκύψει
Δουλεύοντας όμοια με αφαίρεση κατά μέλη προκύπτει ότι g(x)-f(x)=2lnx.
Λύνεις το σύστημα και βρίσκεις τους ζητούμενους τύπους.
Και πως θα βγαλω το προσημο των f(x)+g(x) και g(x)-f(x) για να βγαλω τα απολυτα;
Ευχαριστω παρα πολυ για τη βοηθεια...

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Dias
Επιφανές μέλος


 Τα σημεία Μ1, Μ2, Μ3 είναι εικόνες των μιγαδικών z1, z2, z3 που ικανοποιούν τη σχέση:
Τα σημεία Μ1, Μ2, Μ3 είναι εικόνες των μιγαδικών z1, z2, z3 που ικανοποιούν τη σχέση:
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
djimmakos
Διάσημο μέλος


2) Κάνε κατάλληλες διασπάσεις
3) Κάνε παραγοντοποίηση
4) Σκέψου ότι δεν είσαι στους πραγματικούς.
Αυτά. Τα υπόλοιπα πιστεύω θα τα βρεις και μόνος σου. :p
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Dias
Επιφανές μέλος


Τα έκανα ήδη όλα αυτά. Έβγαλα:1) Πολλαπλασίασε με το 2
2) Κάνε κατάλληλες διασπάσεις
3) Κάνε παραγοντοποίηση
4) Σκέψου ότι δεν είσαι στους πραγματικούς.
Αυτά. Τα υπόλοιπα πιστεύω θα τα βρεις και μόνος σου. :p
(z1 - z2)² + (z2 - z3)² + (z3 - z1)² = 0
Και? Για να είναι ισόπλευρο θα ήθελα να βρω ότι:
|z1 - z2| = |z2 - z3| = |z3 - z1|

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 16 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 231 μέλη διάβασαν αυτό το θέμα:
- ChrisG152
- giorgos5002
- giannis06
- Panagiwths12
- mikke
- hristosdab
- trifasikodiavasma
- haji
- thepigod762
- Mariosm.
- soulatso
- oteletampis
- phleidhs
- Hased Babis
- AggelikiGr
- sir ImPeCaBlE
- veiNqh
- Scandal
- alekos
- Debugging_Demon
- just some guy
- xristosgkm
- ismember
- Apocalypse
- arrow25
- rempelos42
- ggl
- GStef
- QWERTY23
- xrisamikol
- Σωτηρία
- nikoletaz57
- _Aggelos123
- Mariam38
- SlimShady
- strsismos88
- Georgekk
- Lia 2006
- igeorgeoikonomo
- marian
- tsiobieman
- constansn
- Xristosdimitra
- Panagiotis849
- ρενακι 13
- Memetchi
- eukleidhs1821
- Nikkkpat
- Unboxholics
- korlef
- kwstaseL
- Thanos_D
- the purge
- T C
- Giii
- Papachrist
- liaiscool
- Αννα Τσιτα
- globglogabgalab
- Pharmacist01
- thanahss
- abcdefg12345
- nicole1982
- thecrazycretan
- kvstas92
- KingOfPop
- maria301
- papa2g
- stefan
- Κλημεντίνη
- TonyMontanaEse
- Lathy
- Alexecon1991
- Μάρκος Βασίλης
- Cortes
- το κοριτσι του μαη
- calliope
- ale
- panagiotis G
- Kleanth
- aggelosst9
- BioChemical
- spring day
- nucomer
- Georgia110
- LeoDel
- pink_panther
- Alexandros973
- marsenis
- den antexw allh apotyxia
- KaterinaL
- kiyoshi
- drosos
- Λαμπρινηη
- Bill22
- Chrysablac.
- giorgosp97
- Βλα
- Monster Hunter
- jul25
- xxxtolis
- Stroka
- nicks1999
- totiloz
- Earendil
- mitsakos
- tasost
- lnesb
- ssalex
- alan09
- Livaja10
- χημεια4λαιφ
- Viedo
- UncleJ
- Kostakis45
- Infrared
- Zgian
- pepatogourounaki
- hirasawayui
- GeoCommand
- Eleni54
- American Economist
- EiriniS20
- ΘανάσοςG4
- stamoul1s
- Αριάνα123
- uni77
- Libertus
- tasoss
- PanosCh002
- Unseen skygge
- Νικόλας Ραπ.
- cel123
- The Limit Does Not Exist
- don_vito
- suaimhneas
- Αλκης Κ.
- alexrami
- Baggelitsa36
- Νομικάριος13
- spinalgr1990
- d_th
- Adolfo valencia
- Πα.Κ
- Vasilis25
- Johnman97
- Steffie88
- rekcoR
- gwgw_5
- fockos
- Mariahj
- roud
- kostas83
- Cpt.Philips
- Makis45
- Χρησλου
- Panos_02
- Vold
- tymvorixos
- GiorgosAsi
- Neos167
- theodoraooo
- George187
- Άρτεμις Α.
- Μαρία2222
- christos87
- Idontknoww
- jimis2001
- Metamorph
- Γατόπαρδος.
- Johnsk
- mitsos14
- johnsiak
- Elel
- Dreamer_SW
- Γιαννης1987Θεσσ
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki