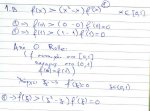α)ψ=0 στην f(x+ψ)= f(χ)+f(ψ)+χημψ+ψημχ => f(x)+f(-x)=2xημχΚαλησπέρα.
ασκ. 60 Μπάρλας 2, σελ 296.
Συνάρτηση f συνεχής στο [-π/2,π/2] για κάθε χ.ψ eR
Ισχύει: f(x+ψ)= f(χ)+f(ψ)+χημψ+ψημχ
α) νδο f(x)+f(-x)=2xημχ
β) να υπολογίσετε το ολοκλήρωμα. (δεν ξέρω να βάζω ψαράκι)
ολοκλήρωμα ορισμένο από π/2 έως -π/2 του f(x)dx
Ευχαριστώ.
β)ολοκλήρωσε τη σχέση αυτή και χώρισε το ολοκήρωμα του αριστερού μέλους στα 4 επιμέρους: της f(x) και f(-x) από -π/2 έως 0 και από ο έως π/2.
Αλλαγή μεταβλητής στο στα ολοκληρώματα με f(-x): u=-x du=-dx.
Τελικά βρίσκεις το ολοκλήρωμα ίσο με 2 αν το έκανα σωστά.
f συνεχής στο [α,β] άρα έχει ένα μέγιστο (M στο χ_μ) και ένα ελάχιστο (m στο χ_ε) στο [α,β]: m=f(x_ε)=<f(x)=<f(x_μ)=Μ.1.Θεωρούμε τις συνεχείς συναρτήσεις f,g:[α,β]->R.Αν για καθε χε[α,β] ισχύει g(x)>0 νδο υπάρχει ξε(α,β) ωστεg(x)dx=f(\xi ) \int_{\alpha }^{\beta }g(x)dx)
Πολλαπλασιάζουμε με την g(x). Επειδή είναι θετική δεν αλλάζει η φορά της ανισότητας και φεύγουν τα "=" (αφού g όχι 0): mg(x)<f(x)g(x)<Μg(x). Άρα ισχύει και η mΣg(x)<Σf(x)g(x)<ΜΣg(x), όπου Σ το ολοκλήρωμα ως προς χ από α έως β.
Διαιρούμε με Σg(x) και έχουμε: m=f(x_ε)<(Σf(x)g(x))/Σg(x)<f(x_μ)=M.
Από το θεώρημα ενδιαμέσων τιμών έχεις ότι υπάρχει ένα ξ στο (χ_ε,χ_μ) που είναι όμως υποσύνολο του (α,β) για το οποίο ισχύει f(ξ)=Σf(x)g(x))/Σg(x).
Και το ζητούμενο απεδείχθη.
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
χρηστοσ17
Νεοφερμένο μέλος


f''(x)=2/(x-1)^3
εχει ασυμπτ. οταν χ--> +00
την 27χ+y-1=0
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Harry0000
Εκκολαπτόμενο μέλος


Μεγαλη χαρη σου κανω
Ευχαριστώ πολύ
β. Ένα κινητό κινείται στην καμπύλη f(x)=lnx. Καθώς περνάει από το σημείο Α(e^1/2 , 1/2) η τετμημένη του x ελαττώνεται με ρυθμό 2 μονάδες ανά sec. Να βρείτε το ρυθμό μεταβολής της γωνίας θ=MOX , τη χρονική στιγμή που το κινητό περνάει από το Α.
Μήπως μπορεί να με βοηθήσει κανείς;
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
forakos
Νεοφερμένο μέλος


α)ψ=0 στην f(x+ψ)= f(χ)+f(ψ)+χημψ+ψημχ => f(x)+f(-x)=2xημχ
β)ολοκλήρωσε τη σχέση αυτή και χώρισε το ολοκήρωμα του αριστερού μέλους στα 4 επιμέρους: της f(x) και f(-x) από -π/2 έως 0 και από ο έως π/2.
Αλλαγή μεταβλητής στο στα ολοκληρώματα με f(-x): u=-x du=-dx.
Τελικά βρίσκεις το ολοκλήρωμα ίσο με 2 αν το έκανα σωστά.
f συνεχής στο [α,β] άρα έχει ένα μέγιστο (M στο χ_μ) και ένα ελάχιστο (m στο χ_ε) στο [α,β]: m=f(x_ε)=<f(x)=<f(x_μ)=Μ.
Πολλαπλασιάζουμε με την g(x). Επειδή είναι θετική δεν αλλάζει η φορά της ανισότητας και φεύγουν τα "=" (αφού g όχι 0): mg(x)<f(x)g(x)<Μg(x). Άρα ισχύει και η mΣg(x)<Σf(x)g(x)<ΜΣg(x), όπου Σ το ολοκλήρωμα ως προς χ από α έως β.
Διαιρούμε με Σg(x) και έχουμε: m=f(x_ε)<(Σf(x)g(x))/Σg(x)<f(x_μ)=M.
Από το θεώρημα ενδιαμέσων τιμών έχεις ότι υπάρχει ένα ξ στο (χ_ε,χ_μ) που είναι όμως υποσύνολο του (α,β) για το οποίο ισχύει f(ξ)=Σf(x)g(x))/Σg(x).
Και το ζητούμενο απεδείχθη.
M στο χ_μ) και ένα ελάχιστο (m στο χ_ε)
Τι είναι τα χ_μ και χ_ε; Διαστήματα;

Ευχαριστω παρα πολυ παντως

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


Παρακαλώ.M στο χ_μ) και ένα ελάχιστο (m στο χ_ε)
Τι είναι τα χ_μ και χ_ε; Διαστήματα;
Ευχαριστω παρα πολυ παντως

Όχι δεν είναι διαστήματα.
Η f επειδή είναι συνεχής έχει μία ελάχιστη τιμή την m και μία μέγιστη την Μ τις οποίες παίρνει για τιμή του χ: χ_ε και χ_μ αντίστοιχα. Δηλαδή: f(x_ε)=m και f(x_μ)=Μ.
Τα ε και μ είναι δείκτες.
Πάντως δε νομίζω να πέσει κάτι τέτοιο στις πανελλήνιες.
----------------------------------------------------------------------
@Harry0000:
Ποια είναι η γωνία θ; Ποια είναι τα σημεία Μ, Ο, Χ;
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Harry0000
Εκκολαπτόμενο μέλος


Πάντως δε νομίζω να πέσει κάτι τέτοιο στις πανελλήνιες.
----------------------------------------------------------------------
@Harry0000:
Ποια είναι η γωνία θ; Ποια είναι τα σημεία Μ, Ο, Χ;
Η γωνία θ είναι η γωνία που ορίζουν οι πλευρές ΜΟ και ΟΧ
Μ είναι το κινητό, Ο η αρχή των αξόνων.
τώρα το Χ δεν ξέρω μάλλον το όποιο σημείο.
Βασικά μας το έδωσε στο σχολείο για ένα διαγώνισμα για το σπίτι......
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


Μάλιστα... Προφανώς τότε έπρεπε να βάλει το χ μικρό και όχι κεφαλαίο γιατί μάλλον εννοεί τον θετικό ημιάξονα των χ.Η γωνία θ είναι η γωνία που ορίζουν οι πλευρές ΜΟ και ΟΧ
Μ είναι το κινητό, Ο η αρχή των αξόνων.
τώρα το Χ δεν ξέρω μάλλον το όποιο σημείο.
Βασικά μας το έδωσε στο σχολείο για ένα διαγώνισμα για το σπίτι......
Λοιπόν:
Ο ρυθμός μεταβολής της τετμημένης ως προς το χρόνος δίνεται: dx/dt=-2
Θέτω y=lnx για διευκόλυνση. Και θ=u
dy/dt=(dy/dx)(dx/dt)=(1/x)(-2)=-2/x
tanu=dy/dx=(dy/dt)(dt/dx)=(-2/x)(1/[-2])=1/x
Παραγωγίζεις αυτή την εξίσωση: (1/(cosu)^2)(du/dt)=(-1/x^2)(dx/dt)=2/x^2=>du/dt=(2/x^2)(cosu)^2.
Όμως (cosu)^2=x^2/(x^2+y^2).
Άρα: du/dt=2/(χ^2+y^2).
Στο σημείο Α(χ,υ)=(e^(1/2),1/2): du/dt=8/(4e+1).
Αυτή είναι η διαδικασία. Ίσως, όμως, να έχω κανένα λάθος στις πράξεις.
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
manouno
Εκκολαπτόμενο μέλος


Μήπως θυμάστε πόσο είναι η παράγωγος της παρακάτω συνάρτησης ??
f(x)=
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
coheNakatos
Δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Harry0000
Εκκολαπτόμενο μέλος


tanu=dy/dx=(dy/dt)(dt/dx)=(-2/x)(1/[-2])=1/x
Παραγωγίζεις αυτή την εξίσωση: (1/(cosu)^2)(du/dt)=(-1/x^2)(dx/dt)=2/x^2=>du/dt=(2/x^2)(cosu)^2.
Όμως (cosu)^2=x^2/(x^2+y^2).
Άρα: du/dt=2/(χ^2+y^2).
Στο σημείο Α(χ,υ)=(e^(1/2),1/2): du/dt=8/(4e+1).
Μήπως μπορείς να μου εξηγήσεις τι έχει κάνει στα υπογραμμισμένα;
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


Αν έχεις την tanf(x), πώς θα την παραγωγίσεις;Μήπως μπορείς να μου εξηγήσεις τι έχει κάνει στα υπογραμμισμένα;
Προφανώς ως εξής: [-1/(cosf(x))^2]*f '(x), έτσι δεν είναι;
Σε αυτήν την περίπτωση έχεις u=u(t).
---
Αν έχεις: y=y(x) και x=x(t) και θέλεις να παραγωγίζεις την y ως προς t, τότε παραγωγίζεις την y ως προς χ και πολλαπλασιάζεις με την παράγωγο του χ ως προς t, άρα: dy/dt=[dy/dx][dx/dt]: κατι που βγαίνει και πολύ εύκολα αν χρησιμοποιήσεις την γραφή του Leibniz και τα διαφορικά ως οποιονδήποτε αριθμό και πολλαπλασιάσεις και διαιρέσεις με το dx.
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Harry0000
Εκκολαπτόμενο μέλος


Αν έχεις την tanf(x), πώς θα την παραγωγίσεις;
Προφανώς ως εξής: [-1/(cosf(x))^2]*f '(x), έτσι δεν είναι;
Σε αυτήν την περίπτωση έχεις u=u(t).
---
Αν έχεις: y=y(x) και x=x(t) και θέλεις να παραγωγίζεις την y ως προς t, τότε παραγωγίζεις την y ως προς χ και πολλαπλασιάζεις με την παράγωγο του χ ως προς t, άρα: dy/dt=[dy/dx][dx/dt]: κατι που βγαίνει και πολύ εύκολα αν χρησιμοποιήσεις την γραφή του Leibniz και τα διαφορικά ως οποιονδήποτε αριθμό και πολλαπλασιάσεις και διαιρέσεις με το dx.
Ευχαριστώ, γιατί είχα ψιλομπερδευτεί....
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
sakishrist
Νεοφερμένο μέλος


Θα ήθελα λίγη βοήθεια με την παρακάτω άσκηση:

Κατ΄αρχάς το πρώτο δεν είναι συνέπεια του κλειστού διαστήματος στο οποίο ορίζεται η συνάρτηση;
Ευχαριστώ εκ των προτέρων
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Συνημμένα
coheNakatos
Δραστήριο μέλος


Γεια σας,
Θα ήθελα λίγη βοήθεια με την παρακάτω άσκηση:
Κατ΄αρχάς το πρώτο δεν είναι συνέπεια του κλειστού διαστήματος στο οποίο ορίζεται η συνάρτηση;
Ευχαριστώ εκ των προτέρων
Για το Α αυτο που ειπες και εσυ
Για το Β μια λυση ειναι ΘΜΤ στα [0,χ] και [χ,1] (πριν βρισκεις οτι f(0)>0 και f(1)>0 με αντικατασταση)
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
sakishrist
Νεοφερμένο μέλος


Ευχαριστώ εκ των προτέρων
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
sakishrist
Νεοφερμένο μέλος


Όσων αφορά το δεύτερο ερώτημα έχω φτάσει μέχρι εδώ και από εκεί και πέρα δεν μου έρχεται τι πρέπει να κάνω.


Once again, thanks in advance!
EDIT: Oops ... έχω και ορθογραφικά εκεί πάνω.

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Συνημμένα
coheNakatos
Δραστήριο μέλος


Πρώτων για το Α ερώτημα από ότι είδα δεν αρκεί να πούμε πως είναι ορισμένη σε κλειστό διάστημα καθώς η αρχική και η τελική τιμή είναι ίσες, άρα θα μπορούσε να είναι σταθερή και άρα να μην παρουσιάζει ακρότατα.
Όσων αφορά το δεύτερο ερώτημα έχω φτάσει μέχρι εδώ και από εκεί και πέρα δεν μου έρχεται τι πρέπει να κάνω.

Once again, thanks in advance!
EDIT: Oops ... έχω και ορθογραφικά εκεί πάνω.
1ον ) το βιβλιο αν δεις τον ορισμο δεν κανει κανει Κανεναν διαχωρισμο για το αν ειναι σταθερη .. επειτα το οτι υπαρχει ξ ωστε f'(j)=0 δεν αρκει ΠΡΕΠΕΙ να αλλαζει το προσημο της f' εκατερωθεν της ριζας !
Για το β Κανεις ΘΜΤ στα διαστηματα που σου ειπα και λυνεις ως προς f(x) Και βγαινει f(x)>(κατι θετικο) !
Π.Σ : Πως βγαινει οτι f(0)=f(1) ?
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


Τι θέλεις να πεις, δηλαδή ότι μία συνάρτηση για να έχει ρίζα κάπου πρέπει να αλλάζει και πρόσημο; Δηλαδή για εσένα η φ(χ)=χ^2 δεν έχει ρίζα;1ον ) το βιβλιο αν δεις τον ορισμο δεν κανει κανει Κανεναν διαχωρισμο για το αν ειναι σταθερη .. επειτα το οτι υπαρχει ξ ωστε f'(j)=0 δεν αρκει ΠΡΕΠΕΙ να αλλαζει το προσημο της f' εκατερωθεν της ριζας !
Για το β Κανεις ΘΜΤ στα διαστηματα που σου ειπα και λυνεις ως προς f(x) Και βγαινει f(x)>(κατι θετικο) !
Π.Σ : Πως βγαινει οτι f(0)=f(1) ?
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
coheNakatos
Δραστήριο μέλος


Τι θέλεις να πεις, δηλαδή ότι μία συνάρτηση για να έχει ρίζα κάπου πρέπει να αλλάζει και πρόσημο; Δηλαδή για εσένα η φ(χ)=χ^2 δεν έχει ρίζα;
Αν ειδες μιλαμε για ακροτατο .. διαβασε και μην βγαζεις συμπερασματα
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
nbp92
Νεοφερμένο μέλος


Αν η f ειναι παραγωγισιμη στο R και η ευθεια y=x-3 εφαπτεται της γραφικης παραστασης της f στο M(0. f(0)) και g(x)=f(x*e^x) για καθε x που ανηκει στο R, τοτε
α) Να υπολογισετε τα f(0), f'(0), g'(0)
β) Να αποδειξετε οτι η ευθεια y=x-3 εφαπτεται και στην γραφικη παρασταση τησ g στο σημειο M(0, f(0))
Ευχαριστω για την βοηθεια σασ
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 0 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 232 μέλη διάβασαν αυτό το θέμα:
- Hased Babis
- ChrisG152
- giorgos5002
- giannis06
- Panagiwths12
- mikke
- hristosdab
- trifasikodiavasma
- haji
- thepigod762
- Mariosm.
- soulatso
- oteletampis
- phleidhs
- AggelikiGr
- sir ImPeCaBlE
- veiNqh
- Scandal
- alekos
- Debugging_Demon
- just some guy
- xristosgkm
- ismember
- Apocalypse
- arrow25
- rempelos42
- ggl
- GStef
- QWERTY23
- xrisamikol
- Σωτηρία
- nikoletaz57
- _Aggelos123
- Mariam38
- SlimShady
- strsismos88
- Georgekk
- Lia 2006
- igeorgeoikonomo
- marian
- tsiobieman
- constansn
- Xristosdimitra
- Panagiotis849
- ρενακι 13
- Memetchi
- eukleidhs1821
- Nikkkpat
- Unboxholics
- korlef
- kwstaseL
- Thanos_D
- the purge
- T C
- Giii
- Papachrist
- liaiscool
- Αννα Τσιτα
- globglogabgalab
- Pharmacist01
- otinanai123
- abcdefg12345
- nicole1982
- thecrazycretan
- kvstas92
- KingOfPop
- maria301
- papa2g
- stefan
- Κλημεντίνη
- TonyMontanaEse
- Lathy
- Alexecon1991
- Μάρκος Βασίλης
- Cortes
- το κοριτσι του μαη
- calliope
- ale
- panagiotis G
- Kleanth
- aggelosst9
- BioChemical
- spring day
- nucomer
- Georgia110
- LeoDel
- pink_panther
- Alexandros973
- marsenis
- den antexw allh apotyxia
- KaterinaL
- kiyoshi
- drosos
- Λαμπρινηη
- Bill22
- Chrysablac.
- giorgosp97
- Βλα
- Monster Hunter
- jul25
- xxxtolis
- Stroka
- nicks1999
- totiloz
- Earendil
- mitsakos
- tasost
- lnesb
- ssalex
- alan09
- Livaja10
- χημεια4λαιφ
- Viedo
- UncleJ
- Kostakis45
- Infrared
- Zgian
- pepatogourounaki
- hirasawayui
- GeoCommand
- Eleni54
- American Economist
- EiriniS20
- ΘανάσοςG4
- stamoul1s
- Αριάνα123
- uni77
- Libertus
- tasoss
- PanosCh002
- Unseen skygge
- Νικόλας Ραπ.
- cel123
- The Limit Does Not Exist
- don_vito
- suaimhneas
- Αλκης Κ.
- alexrami
- Baggelitsa36
- Νομικάριος13
- spinalgr1990
- d_th
- Adolfo valencia
- Πα.Κ
- Vasilis25
- Johnman97
- Steffie88
- rekcoR
- gwgw_5
- fockos
- Mariahj
- roud
- kostas83
- Cpt.Philips
- Makis45
- Χρησλου
- Panos_02
- Vold
- tymvorixos
- GiorgosAsi
- Neos167
- theodoraooo
- George187
- Άρτεμις Α.
- Μαρία2222
- christos87
- Idontknoww
- jimis2001
- Metamorph
- Γατόπαρδος.
- Johnsk
- mitsos14
- johnsiak
- Elel
- Dreamer_SW
- Γιαννης1987Θεσσ
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki