Βοήθεια/Aπορίες στα Μαθηματικά Προσανατολισμού

[kvgreco]

Βασικα και εγω ετσι την ελυσα..αλλα εχω μια απορια..στην συναρτηση που εχουμε θεσει κανοντας bolzano...λεμε οτι f(a)-a>=0 και f(b)<=0..για να πεις τελικα οτι το γινομενο ειναι μικροτερο η ισο του μηδενος..αλλα απο Θ.μεγιστης ελαχιστης τιμης αφου η f ειναι συνεχης συναρτηση δεν ισχυει οτι f(a)=a k f(b)=b..?

Δεν νομίζω ότι αυτό λέει το θεώρημα μέγιστης και ελάχιστης τιμής.Απλά γιά μιά συνεχή συνάρτηση η εικόνα ενός κλειστού διαστήματος είναι ένα κλειστό διάστημα που σημαίνει άρα ότι η f(x) παρουσιάζει ολικά ακρότατα αλλά δεν προκύπτει κατ ανάγκη από κάπου ότι f(a)=a k f(b)=b.Αν π.χ η συνάρτηση ειναι γνησίως φθίνουσα τότε θα ισχύει f(a)=b και f(b)=a! Ή είναι ακόμη δυνατόν να ισχύει f(a)=f(b).Αν κάνω λάθος ας με διορθώσει κάποιος ειδικός.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[KONNOS]

Ναι οκ λαθος εκανα..η ασκηση παει κανονικα με bolzano..

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[kvgreco]

Πώς υπολογίζεται ρε παιδιά το παρακάτω ολοκλήρωμα;

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[manos66]

Πώς υπολογίζεται ρε παιδιά το παρακάτω ολοκλήρωμα;

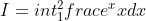
Δεν υπολογίζεται με μεθόδους που ξέρετε

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[In Flames]

βασικα οντως προσπαθησα με καθε μεθοδο που ηξερα και δε μου βγηκε κατι.

υπαρχει και κατι ακομη που αν αποδειξεις δεν ξερω αν σου βγει:
ολοκληρωμα απο b σε a της H(x)dx= ολοκληρωμα απο b σε a της H(a+b-x)dx
δε νομιζω να βγαινει ετσι ομως

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[mostel]

Γενικώς αυτά υπολογίζονται προσεγγιστικά (βλ σειρές Taylor/McLaurin). Δεν παίζει να μπει κάτι τέτοιο εξετάσεις. Μη τα ψιρίζετε τόσο πολύ.... Λύστε εύκολα θέματα, γιατί αν την πατήσετε, εκεί θα την πατήσετε

Τώρα, για τη συγκεκριμένη συνάρτηση, για τους περίεργους:

https://en.wikipedia.org/wiki/Exponential_integral


- Στέλιος

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[kvgreco]

Γενικώς αυτά υπολογίζονται προσεγγιστικά (βλ σειρές Taylor/McLaurin). Δεν παίζει να μπει κάτι τέτοιο εξετάσεις. Μη τα ψιρίζετε τόσο πολύ.... Λύστε εύκολα θέματα, γιατί αν την πατήσετε, εκεί θα την πατήσετε

Τώρα, για τη συγκεκριμένη συνάρτηση, για τους περίεργους:

https://en.wikipedia.org/wiki/Exponential_integral


- Στέλιος

Στέλιο δεν το πολυψάχνω αλλά μάλλον παίζει με το πόνο μας ο καθηγητής.Ίσως όμως να είναι καλό έτσι γιατί εμείς νομίζαμε πως όλα τα ολοκληρώματα βγαίνουν με τις γνωστές μεθόδους.Μας είπε ο άνθρωπος ότι δεν μπορούμε εμείς να το βγάλουμε.Αλλά το πείσμα, πείσμα.Έχασα κάμποση ώρα με αυτό το ολοκλήρωμα.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[leobakagian]

Μπορεί κάποιος να μου πει τους τύπους τριγωνομετρία που χρειάζονται για την φυσική κατ και τα μαθ κατ στην 3η λυκείου;

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[baki]

βασικα ολοι χρειαζονται

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[cheery]

Η τριγωνομετρία και οι λογάριθμοι είναι τα πιο βασικά κεφάλαια (απο την ύλη της β) για για την γ λυκ

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[mtsilp]

Μπορείς να δεις ένα τυπολόγιο στη διεύθυνση
https://www.emathisis.gr/course/category.php?id=7

(στείλε πρώτα τη φόρμα δωρεάν εγγραφής στη Β΄ Λυκείου https://www.emathisis.gr/form88446/form.html)

Στο www.emathisis.gr υπάρχει πληθώρα υλικού -κυρίως για τα μαθηματικά - για το Λύκειο.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[ΓιώργοςΒ]

:no1:

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[_ann_]

να ρωτησω κατι?...εχουμε την:


μπορω να πω οτι ο τυπος της ειναι ο F(x) = lnx - ln1?
και αν οχι ,γιατι δεν μπορω?

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[ΛΑΓΟΔΗΜΟΣ ΜΑΡΙΟΣ]

αν θές το f΄ θα είναι 1 δια χ σύμφωνα με γνωστή ιδίοτητα τώρα την παράγουσα δεν μπορείς βρείς αφού θα πρέπει να βρείς μια συνάρτηση που αν την παραγωγίσεις να πέρνεις το ολοκλήρωμα αλλά δεν ξέρεις μια τέτοια συνάρτηση αφου την f την έχεις ως προς χ ενώ το ολοκλήρωμα είναι ως προς t !!!!!!! αυτό που έχεις γράψει αν παραγωγιστεί δίνει 1 δια χ και όχι την F(χ)

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[_ann_]

και κατι ακομα..
αν εχω την

μπορω να πω οτι F(x) =


αν οχι..γιατι?
-----------------------------------------
αυτο που εχω γραψει αν παραγωγισθει δινει το 1/χ που ειναι σωστο..δεν καταλαβαινω γιατι δεν μπορω να βρω την F με τον γνωστο τροπο απο τα ορισμενα...μεταβλητη θεωρουμε το t η το x?του ολοκληρωματος το t και ως προς την F το x..σωστα?

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Xenofon]

Μπορείς να το κάνεις και στις 2 περιπτώσεις. Τα ορισμένα ολοκληρώματα με μεταβλητά άκρα είναι όπως τα ορισμένα ολοκληρώματα με αριθμούς στα άκρα. Δεν υπάρχει πρόβλημα να ακολουθήσεις το Θεμελιώδες Θεώρημα του Ολοκληρωτικού Λογισμού ότι και να έχεις στο άκρο. Ωστόσο, πρέπει να προσέξεις στη 2η περίπτωση, εάν θέλεις να παραγωγήσεις τη F τότε θα πρέπει να φέρεις το ολοκλήρωμα στη μορφή που έχει και το θεώρημα, δηλαδή με συνάρτηση του x ΜΟΝΟ στο πάνω άκρο σπάζοντας και κάνοντας τις κατάλληλες τροποποιήσεις.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[_ann_]

ευχαριστω!αλλη μια απορια...πως βγαζουμε το συμπερασμα οτι αν η f΄ ειναι συνεχεις τοτε η F ειναι παραγωγισιμη?(ισχυει και το αντιστροφο?)δεν το λεει καπου η θεωρια..θα πρεπει αν ζητηθει να αποδειχθει δλδ?

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[bomberman13]

φ(Χ)=lnχ ή φ(χ)=ln(-x)

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[bomberman13]

αν θέσεις u=lnx δε γίνεται τίποτα?

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[katerinaisc]

να δείξετε οτι f(x)=x/(x^2+4) εχει τρία σημεία καμπής τα οποία ειναι συνευθειακά.
Κ το πεδιο ορισμου της f.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.