Βοήθεια/Aπορίες στα Μαθηματικά Προσανατολισμού

mostel · 26-10-07

Αρχική Δημοσίευση από exc:
Άσκηση:
Σας δίνω την παρακάτω σχέση: $f(x)=x^2+2|z_1-z_2|x+(1+|z_1|^2)(1+|z_2|^2)$ , όπου $z_1,z_2in C$ .
Νδο $f(x)ge0$ , για κάθε $xin R$ .

Είναι κλασική άσκηση. Έχουν τεθεί παρόμοιες κατά καιρούς σε περιοδικά της Ε.Μ.Ε. Αν δεν απατώμαι, η άσκηση αυτούσια υπάρχει στο βοηθητικό του Στεργίου-Νάκη. Η λύση είναι απλή. Αρκεί να δείξουμε ότι η διακρίνουσα του παραπάνω τριωνύμου είναι αρνητική.

exc · 26-10-07

Δεν έχω καταλάβει γιατί αν η διακρίνουσα (στην συγκεκριμένη περίπτωση) είναι αρνητική ισχύει αυτό που ζητάται να αποδειχθεί. Τέτοια άσκηση εμείς δεν λύσαμε στο σχολείο, δεν πηγαίνω και σε φροντηστήριο και την είδα πρώτη φορά χθές στο διαδίκτυο και δεν μπορούσα να τη λύσω. Σκέφτηκα, όμως, ότι ο mostel θα βοηθήσει...:xixi:
===
edit: Εντάξει, κατάλαβα γιατί...

mostel · 26-10-07

Απλώς το σημείο που πρέπει να προσέξεις εδώ είναι άλλο. Σου λέει μεγαλύτεορ ίσο. Αν έλεγε μόνο "μεγαλύτερο" τότε θα αρκούσε να δείξεις ότι η διακρίνουσα σου είναι αρνητική. Επειδή μας λέει και ίσο, θα πρέπει να βρούμε για ποια τιμή της διακρίνουσάς του τριωνύμου, το πολυώνυμο έχει λύση. Θέλει λίγο προσοχή!

Δες μία από έναν Ευκλείδη του 1979, η οποία είναι παρόμοια με την προηγούμενη, άλλα λίγο πιο δύσκολη:

Έστω οι μιγαδικοί $z_1=a+bi$ και $z_2=c+di$ , με $a,b,c,d$ θετικούς αριθμούς ώστε $|z_1|=|z_2|=1$ . Έστω η εξίσωση: $x^2-2|z_1-z_2|x+2=0$ , που έχει ρίζες $x_1,x_2$ . Να δείξετε ότι:

i) Οι ρίζες $x_1,x_2$ δεν είναι πραγματικές.
ii) Ισχύει: $|x_1|=|x_2|=\sqrt{2}$
iii) Ισχύει: $|x_1-x_2|^2+4|z_1-z_2|^2=8$ .
iv) Ο μιγαδικός $w=\frac{x_1}{x_2}+\frac{x_2}{x_1}$ είναι πραγματικός και να βρεθεί η μικρότερη τιμή του.

exc · 27-10-07

Mostel, δώσε τις λύσεις των iii & iv να δω αν καταλάθος τα έλυσα σωστά...:xixi: Ολόκληρες τις απαντήσεις, αν μπορείς, για να δω και τον τρόπο με τον οποίο τα έλυσες σε περίπτωση που τα έχω λύσει λανθασμένα...

mostel · 27-10-07

Έχουμε και λέμε:

Για το i)

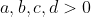
Παίρνεις διακρίνουσα, κάνεις πράξεις, αντικατάσταση των μιγαδικών με την διανυσματική τους μορφή, όπως δίδεται στην εκφώνηση και καταλήγεις στο $D=-8(ac+bd)<0$ (επειδή $a,b,c,d>0$ ). Άρα, επειδή η διακρίνουσα είναι αρνητική, δε δύναται να 'χει πραγματικές λύσεις η εξίσωση.

Για το ii)

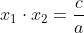
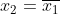
Επειδή οι ρίζες τις εξίσωσεις θα 'ναι μιγαδικές, θα 'ναι και συζυγείς μεταξύ τους. Από Vieta ισχύει: $x_1\cdot x_2=\frac{c}{a}$ . Όμως $x_2=\overline{x_1}$ . Άρα $x_1\cdot\overline{x_1}=2$ . Έτσι προκύπτει: $|x_1|=\sqrt{2}$ .

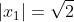
Για το iii)
$<br /> |x_1-x_2|^2=|x_1|^2+|x_2|^2-2Re(x_1\overline x_2)\stackrel{(ii)}{=} 2 + 2 -2\frac{x_1\cdot\overline{x_2}+\overline{x_2}\cdot x_1}{2}=\\=4-(x_1^2-x_2^2)=4-\left( (x_1+x_2)^2-2x_1\cdot x_2\right)=4-(4|z_1-z_2|^2-4)=8-4|z_1-z_2|^2$ .

Άρα $|x_1-x_2|^2 + 4|z_1-z_2|^2=8-4|z_1-z_2|^2+4|z_1-z_2|^2=8$ .

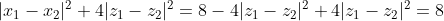
Για το iv)

Το να δείξεις ότι είναι πραγματικός, πάρε το συγυζή του, κάνε αντικατάσταση τα συζυγή με την άλλη ρίζα της εξίσωσης (αφού οι ρίζες είναι συζυγείς) και προκύπτει εύκολα το ζητούμενο. Τώρα για το δεύτερο σκέλος:

$w=\frac{x_1}{x_2}+\frac{x_2}{x_1}=\frac{x_1^2+x_2^2}{x_1\cdot x_2}=\frac{(x_1+x_2)^2-2x_1\cdot x_2}{x_1\cdot x_2}\stackrel{vieta}{=}\frac{4|z_1-z_2|^2-4}{2}=2|z_1-z_2|^2-2$ .

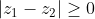
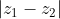
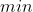
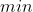
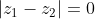
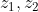
Ψάχνουμε όμως την ελάχιστη τιμή. Όμως $|z_1-z_2|\geq0$ . Επομένως, ψάχνουμε πότε το $|z_1-z_2|$ γίνεται $min$ . Αυτό γίνεται $min$ , όταν $|z_1-z_2|=0$ , το οποίο είναι δυνατόν να ισχύει αφού τα $z_1,z_2$ , κινούνται σε μοναδιαίο κύκλο και αυτό επιτυγχάνεται όταν συμπίπτουν.

exc · 28-10-07

Είμαι βαθύτατα συγκινημένος... :'(

Έλυσα σωστά την άσκηση!

Πάντως mostel, δεν βρίσκω καμία ομοιότητα ανάμεσα στις δύο ασκήσεις και αυτός ήταν ο λόγος που νόμιζα ότι είχα κάνει λάθος.

mostel · 28-10-07

Διακρίνουσα κλπ... δεν έχει πραγματικές λύσεις, άρα το τριώνυμο είναι θετικό στους πραγματικούς

!Δημητρα! · 31-10-07

View attachment 1.doc
Θα ηθελα αν μπορει καποιος να μου λυσει τις ασκησεις γιατι με μπερδεψαν..
ΤHANKS!

exc · 31-10-07

1)1)Εδώ το πρώτο βγαίνει από τον τύπο της 2βαθμιας εξίσωσης στο σύνολο των μιγαδικών: Οι δύο ρίζες είναι συζυγείς: $x_{1,2}=\frac{-b\pm i\sqrt{D}}{2a}$ . Για το άλλο: Ξέρεις πλέον ότι οι ρίζες της 2βαθμιας είναι συζυγείς. Πρέπει να "παίξεις" με τους τύπους του Vieta οι οποίοι είναι: $x_1+x_2=-\frac{b}{a}$ και $x_1*x_2=\frac{g}{a}$ , όπου $x_1 & x_2$ οι ρίζες της εξίσωσης.
2)Δεν μπορώ να τη λύσω, έχουμε κάνει μόνο μέχρι και τους μιγαδικούς λόγω καταλήψεων.
3)Γνωρίζουμε ότι: $\overline{w}=-w \Leftrightarrow w\in{I}$ (είναι ευνόητη η απόδειξη), συνεπώς αντικαθιστάς το w στην $\overline{w}=-w$ , φτάνεις σε μία απλή μορφή χωρίς κλάσματα κλπ, θέτεις $z=x+yi$ και φτάνεις στον κύκλο που θέλεις. Ο οποίος σε αυτήν την περίπτωση είναι ο $(K(0,1),r=\sqrt{3})$ , αν έκανα σωστά τις πράξεις.

Επίτηδες δεν σου δίνω ολόκληρες απαντήσεις, για να ασχοληθείς εσύ ο ίδιος με την άσκηση, αλλά και γιατί κουράζομαι με το $\LaTeX$

nova · 07-11-07

Για τη 2η

α) $f(f(x))+f(x)=2x+3$

Για $x_1,x_2 \in R$ με $f(x_1)=f(x_2) \ (1)$ έχουμε

$f(f(x_1)) = f(f(x_2)) \ (2)$

Προσθέτοντας τις $(1),(2)$ κατά μέλη παίρνουμε

$f(f(x_1)) +f(x_1)= f(f(x_2))+f(x_2)\Rightarrow$

$2x_1+3 = 2x_2+3 \Rightarrow$

$x_1= x_2$

Άρα η f είναι "1-1"

β) $f(2x^3+x)=f(4-x)$
Αφού η f είναι "1-1" έχουμε $2x^3+x = 4-x \Leftrightarrow$

$2(x^3+x-2)=0$

Προφανής λύση το $x=1$ και μετά από Horner βρίσκουμε ότι $x^3+x-2=(x-1)(x^2+x+2)$

Το τριώνυμο στην παρένθεση δεν παραγοντοποιείται, άρα μοναδική λύση το $x=1$

exc · 12-11-07

Άσκηση σε διαγώνισμα που γράψαμε σήμερα:
$3z\overline{z}^7+2\overline{z}z^7=5$
νδο
a// $z\overline{z}^7=1$
b// $|z|=1$
c//Δεν θυμάμαι...

Οκ. Για το δεύτερο χρησιμοποιούμε το πρώτο. Αν μετά χρησιμοποιήσουμε το δεύτερο για να βρούμε το πρώτο είναι σωστό; Εγώ έτσι έκανα, γιατί μας είπε ότι μπορούμε να χρησιμοποιούμε τα αποτελέσματα των υπολοίπων υποερωτημάτων.

Πώς λύνεται χωρίς τη χρήση του δευτέρου το πρώτο;

Scandal · 12-11-07

Αρχική Δημοσίευση από exc:
Πώς λύνεται χωρίς τη χρήση του δευτέρου το πρώτο;

Μην αφήνετε την αβεβαιότητα να σας τυφλώνει και τα εύκολα σας φαίνονται δύσκολα και πολύπλοκα.

$3z\overline{z}^7+2\overline{z}z^7=5$
$5z\overline{z}^7=5$
$z\overline{z}^7=5/5$
$z\overline{z}^7=1$

:iagree:

-petros

mostel · 12-11-07

Αναρωτιέμαι ποιος είναι τυφλός.... :lol:

Scandal · 12-11-07

Αρχική Δημοσίευση από mostel:
Αναρωτιέμαι ποιος είναι τυφλός....

Ναι έχεις δίκιο

(κι εγώ λάθος είμαι μου το είπε στο MSN

).

-petros

mostel · 12-11-07

Αρχική Δημοσίευση από Petros:
Ναι έχεις δίκιο
(κι εγώ λάθος είμαι μου το είπε στο MSN ).

-petros

Δεν είσαι ακριβώς λάθος...

Αρχικά, από τη δοσμένη έχεις:
$<br /> 3z\overline{z}^7 + 2\overline{z}z^7 =5$ (1)

Άρα και η συζυγής παράσταση αυτής θα 'ναι ίση με 5.

Δηλαδή:

$3\overline{z}z^7+2z\overline{z}^7=5$ (2)

Αφαιρείς τις (1) και (2) κατά μέλη και παίρνεις:

$z\overline{z}^7=\overline{z}z^7$

Πας κάνεις αντικατάσταση στην 1 και... άμπρα κατάμπρα

mostel · 13-11-07

Αρχική Δημοσίευση από exc:
Οκ. Για το δεύτερο χρησιμοποιούμε το πρώτο. Αν μετά χρησιμοποιήσουμε το δεύτερο για να βρούμε το πρώτο είναι σωστό; Εγώ έτσι έκανα, γιατί μας είπε ότι μπορούμε να χρησιμοποιούμε τα αποτελέσματα των υπολοίπων υποερωτημάτων.

Πώς λύνεται χωρίς τη χρήση του δευτέρου το πρώτο;

Αλήθεια, το δεύτερο πώς το έδειξες χωρίς να αποδείξεις το πρώτο ;

miv · 13-11-07

Ολα τα προηγουμενα υποερωτηματα χρησιμοποιουνται ως θεωρια, αν δεν λυθουν, κι εφαρμοζονται αναποδεικτα σε ολα τα επομενα.
Αν εχω πχ.
1) Δειξτε χ=υ
2) Δειξτε 1+χ=1+υ

Αν δε δειξεις το πρωτο, αποδεχεσαι απλα οτι ισχυει για το δευτερο και χανεις μονο το βαθμο του 1).

exc · 13-11-07

Σήμερα μπαίνοντας η καθηγήτρια των μαθηματικών, μας λέει "άντε. ρωτήστε με πώς λυνόταν το πρώτο ερώτημα"... Πιθανόν να το θεώρησε δύσκολο και η ίδια...

Αλήθεια, το δεύτερο πώς το έδειξες χωρίς να αποδείξεις το πρώτο ;

Είναι αυτό ακριβώς που λέει ο miv. Βέβαια εγώ το προχώρησα λίγο και απέδειξα και το πρώτο, αλλά δε νομίζω να επιτρέπεται αυτό που έκανα: απέδειξα το δεύτερο βάσει του πρώτου και το πρώτο βάσει του δεύτερου...

miv · 13-11-07

Το πρωτο οχι, αποδεικνυεται ανεξαρτητα. Λαθος ηταν που απεδειξες το πρωτο βαση του δευτερου. Αποδεικνυεις το δευτερο με βαση το πρωτο, το τριτο με βαση τα 1,2, το τεταρτο με βαση 1,2,3 και παει λεγοντας, αλλα ΠΟΤΕ το αντιστροφο.

mostel · 13-11-07

Αρχική Δημοσίευση από exc:
Σήμερα μπαίνοντας η καθηγήτρια των μαθηματικών, μας λέει "άντε. ρωτήστε με πώς λυνόταν το πρώτο ερώτημα"... Πιθανόν να το θεώρησε δύσκολο και η ίδια...

Είναι αυτό ακριβώς που λέει ο miv. Βέβαια εγώ το προχώρησα λίγο και απέδειξα και το πρώτο, αλλά δε νομίζω να επιτρέπεται αυτό που έκανα: απέδειξα το δεύτερο βάσει του πρώτου και το πρώτο βάσει του δεύτερου...

Πιθανόν να μη μπορούσε να το λύσει και η ίδια, αλλά αναγκάστηκε να κάνει copy/paste την άσκηση από κάνα βοήθημα :lol:

Βοήθεια/Aπορίες στα Μαθηματικά Προσανατολισμού

Πολύ δραστήριο μέλος

Διάσημο μέλος

Πολύ δραστήριο μέλος

Διάσημο μέλος

Πολύ δραστήριο μέλος

Διάσημο μέλος

Πολύ δραστήριο μέλος

Νεοφερμένος

Διάσημο μέλος

Νεοφερμένος

Διάσημο μέλος

Διαχειριστής

Πολύ δραστήριο μέλος

Διαχειριστής

Πολύ δραστήριο μέλος

Πολύ δραστήριο μέλος

Επιφανές μέλος

Διάσημο μέλος

Επιφανές μέλος

Πολύ δραστήριο μέλος