Mr.Blonde
Πολύ δραστήριο μέλος


Θεσε u=lnx....καποιος??
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


After?
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Mr.Blonde
Πολύ δραστήριο μέλος


Eιναι γνωστο οριο και κανει -απειρο.Ναι θα βγει lim(u-->o)[lnu]
After?
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Polymnia
Πολύ δραστήριο μέλος


Θα ήθελα ένα ξεκαθάρισμα σχετικά με το τελευταίο ερώτημα.
Απο προηγουμενα ερωτήματα βρήκα τα εξής :
Για τον μιγαδικό βρήκα οτι ο γτ της εικόνας του είναι κύκλος με κεντρο το σημείο Κ(0,2) και ακτίνα ρ=1 .
Για τον μιγαδικό διαπίστωσα οτι ο γτ της εικόνας του είναι ο κύκλος με κεντρο Λ(4,5) και ακτίνα Ρ=2 .
Απέδειξα οτι
Το τελευταίο ερώτημα ζητά να αποδείξω τούτο :
Έχω προσέξει ,οτι παρ'ολο δεν έχω θέμα γενικά με τους μιγαδικους,με προβληματίζουν ερωτήματα που ζητούν το \left| z+w\right| .
Όταν ζητεί πχ.
Εδώ όμως ,τί γίνεται;
Αν μπορεί κάποιος ας μου το ξεκαθαρίσει,θέλω πιο πολύ να το καταλάβω για τα καλά και όχι απλά να πάρω μια λύση και να το αντιγράψω...

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Για να θυμάσαι τα όρια βασικών συναρτήσεων προσπάθησε να έχεις μία εικόνα της γραφικής παράστασης.Ναι θα βγει lim(u-->o)[lnu]
After?

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Αν το μόνο που σου ζητάει είναι άνω και κάτω φράγμα για το μέτρο τότε η τριγωνική ανισότητα δουλεύει μια χαρά απ' όσο έχω δει. Εφόσον γνωρίζουμε από προηγούμενα ερωτήματα τους αριθμούςΛοιπόν παίδες,είναι μια άσκηση ,συνδυαστική με όρια,συναρτήσεις και μιγαδικούς.
Θα ήθελα ένα ξεκαθάρισμα σχετικά με το τελευταίο ερώτημα.
Απο προηγουμενα ερωτήματα βρήκα τα εξής :
Για τον μιγαδικό βρήκα οτι ο γτ της εικόνας του είναι κύκλος με κεντρο το σημείο Κ(0,2) και ακτίνα ρ=1 .
Για τον μιγαδικό διαπίστωσα οτι ο γτ της εικόνας του είναι ο κύκλος με κεντρο Λ(4,5) και ακτίνα Ρ=2 .
Απέδειξα οτι
Το τελευταίο ερώτημα ζητά να αποδείξω τούτο :
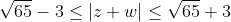
Έχω προσέξει ,οτι παρ'ολο δεν έχω θέμα γενικά με τους μιγαδικους,με προβληματίζουν ερωτήματα που ζητούν το \left| z+w\right| .
Όταν ζητεί πχ.νταξει ,εκεί το βρίσκω και μάλιστα με 3 διαφορετικούς τρόπους .
Εδώ όμως ,τί γίνεται;
Αν μπορεί κάποιος ας μου το ξεκαθαρίσει,θέλω πιο πολύ να το καταλάβω για τα καλά και όχι απλά να πάρω μια λύση και να το αντιγράψω...

Για την δεξιά ανισότητα είναι
ενώ για την αριστερή ανισότητα
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Polymnia
Πολύ δραστήριο μέλος


Αν το μόνο που σου ζητάει είναι άνω και κάτω φράγμα για το μέτρο τότε η τριγωνική ανισότητα δουλεύει μια χαρά απ' όσο έχω δει. Εφόσον γνωρίζουμε από προηγούμενα ερωτήματα τους αριθμούςκαι
πρέπει να τους εμφανίσουμε στην τριγωνική ανισότητα με κατάλληλες προσθαφαιρέσεις. Αναλυτικά έχουμε:
+(w-4-5i)+4+7i\right|)
Για την δεξιά ανισότητα είναι
ενώ για την αριστερή ανισότητα
+(w-4-5i)+4+7i\right| \geq \left||4+7i|-\left|(z-2i)+(w-4-5i)\right|\right| \geq |4+7i|-\left|(z-2i)+(w-4-5i)\right| \geq |4+7i|-|z-2i|-|w-4-5i|=\sqrt{65}-3)
Άρα με τριγωνική βγαίνει.Τι μου ελεγαν οτι δεν μπορώ να αξιοποιήσω την τριγωνική .
Η ολοκληρωμένη εκφώνηση είναι :
Δίνεται συνάρτηση
για την οποία ισχύει : οριο της g(x) όταν το χ τείνει στο +απειρο ειναι ισο με
α) Να βρείτε το
β) Για
και επίσης οτι
Δίνονται επίσης οι μιγαδικοί
για την οποία ισχύουν :
οριο της f(x) όταν το χ τείνει στο +απειρο ειναι ίσο με
α)Να αποδείξετε οτι ο γτ της εικονας του ειναι ο κύκλος με κέντρο το σημείο K
β)Να βρείτε το γτ της εικόνας του
γ)Να αποδείξετε οτι
δ) Να αποδείξετε οτι
Την άσκηση την έλυσα ολη εκτος απο το δ που ρώτησα ,αν και το ειχα λυσει στο προχειρο με ανισοτητα .Απλα ανεβασα ολο το θεμα για να δειτε αν χρειαζεται κατι για το ερωτημα που ρωτησα,αν και δε νομιζω .
Κάπου είχα διαβάσει οτι απαιτούνται κάποιες προυποθέσεις ωστε να χρησιμοποιήσει κανεις τριγωνικη ανισοτητα στους μιγαδικούς.Ισχύει κάτι τέτοιο ή μπορώ να λυσω το ερωτημα χωρις να γραψω τιποτα παραπάνω;

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
mary-blackrose
Εκκολαπτόμενο μέλος


lim(x--> +00) [ln(1/x)]
[LATEX]\Theta \epsilon \tau \omega \quad \frac { 1 }{ x } =\kappa \quad \quad \tau \o \quad x\rightarrow +\infty \quad \tau \o \quad \kappa \rightarrow 0\\ \Leftrightarrow x\cdot \kappa =1\\ \Leftrightarrow x=\frac { 1 }{ \kappa \\ } \\ \varepsilon \pi \o \mu \varepsilon \nu \omega \varsigma \quad \lim _{ \kappa \rightarrow 0 }{ \ln { \frac { 1 }{ \kappa } } } =-\infty \quad \\[/LATEX]Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Δεν γνωρίζω κάποια προϋπόθεση. Είναι άλλωστε στοιχειώδης. Χρησιμοποίησέ την άφοβα.Κάπου είχα διαβάσει οτι απαιτούνται κάποιες προυποθέσεις ωστε να χρησιμοποιήσει κανεις τριγωνικη ανισοτητα στους μιγαδικούς.Ισχύει κάτι τέτοιο ή μπορώ να λυσω το ερωτημα χωρις να γραψω τιποτα παραπάνω;
Άλλος τρόπος χωρίς τριγωνική ανισότητα είναι να παρατηρήσεις ότι ο γ.τ. του
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lowbaper92
Πολύ δραστήριο μέλος


Μήπως εννοείς ότι η τριγωνική ανισότητα εξασφαλίζει μόνο φράγματα, και όχι μέγιστες/ελάχιστες τιμές?Κάπου είχα διαβάσει οτι απαιτούνται κάποιες προυποθέσεις ωστε να χρησιμοποιήσει κανεις τριγωνικη ανισοτητα στους μιγαδικούς.Ισχύει κάτι τέτοιο ή μπορώ να λυσω το ερωτημα χωρις να γραψω τιποτα παραπάνω;
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Polymnia
Πολύ δραστήριο μέλος


Μάλιστα!Δεν γνωρίζω κάποια προϋπόθεση. Είναι άλλωστε στοιχειώδης. Χρησιμοποίησέ την άφοβα.
Άλλος τρόπος χωρίς τριγωνική ανισότητα είναι να παρατηρήσεις ότι ο γ.τ. τουείναι ο κύκλος με κέντρο
και ακτίνα
και δουλεύεις γεωμετρικά.
Θα τη λύσω και γεωμετρικά,όπως είπες.
Σε ευχαριστώ για άλλη μια φορά για την πολύτιμη βοήθειά σου!

Μήπως εννοείς ότι η τριγωνική ανισότητα εξασφαλίζει μόνο φράγματα, και όχι μέγιστες/ελάχιστες τιμές?
Ναι αυτό εννοώ φίλτατε.Είναι σωστό ;

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


Code:[LATEX]\Theta \epsilon \tau \omega \quad \frac { 1 }{ x } =\kappa \quad \quad \tau \o \quad x\rightarrow +\infty \quad \tau \o \quad \kappa \rightarrow 0\\ \Leftrightarrow x\cdot \kappa =1\\ \Leftrightarrow x=\frac { 1 }{ \kappa \\ } \\ \varepsilon \pi \o \mu \varepsilon \nu \omega \varsigma \quad \lim _{ \kappa \rightarrow 0 }{ \ln { \frac { 1 }{ \kappa } } } =-\infty \quad \\[/LATEX]
Ναι,το ελυσα τελικα. Σε ευχαριστω
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


Διπλα στο ημιτονο δν ειναι ημ2x αλλα ημιτονο τετραγωνο του χ
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lowbaper92
Πολύ δραστήριο μέλος


Ναι αυτό εννοώ φίλτατε.Είναι σωστό ;
Ναι, η τριγωνική ανισότητα εξασφαλίζει μόνο φράγματα, και όχι μέγιστες/ελάχιστες τιμές.
Αν έχεις το βοήθημα Στεργίου-Νάκης πήγαινε σελίδα 53 (1ο τεύχος) για να το δεις.
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


Lim(x-->0) [(ημ^2x /x)* συν(1/χ)]
Διπλα στο ημιτονο δν ειναι ημ2x αλλα ημιτονο τετραγωνο του χ
?
δεν εχω καταλάβει παιδιά τις "μηδενικες επι φραγμενες" με τα απολυτα π βαζεις μετα κτλ.οποιος μπορει χελπ
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


Lim(x-->0) [(ημ^2x /x)* συν(1/χ)]
Διπλα στο ημιτονο δν ειναι ημ2x αλλα ημιτονο τετραγωνο του χ
lim(x->0)(((ημx)^2)/(x^2))=(lim(x->0)(ημx/x))^2=1^2=1
lim(x->0)(((ημx)^2)/x)=lim(x->0)[(((ημx)^2)/(x^2))*x]=lim(x->0)(((ημx)^2)/(x^2))*lim(x->0)x=1*0=0
lim(x->0)(((ημx)^2)/x)=0 <=> lim(x->0-)(((ημx)^2)/x)=lim(x->0+)(((ημx)^2)/x)=0
Για κάθε x ανήκει R* έχουμε:
|(((ημx)^2)/x)συν(1/x)|=|(((ημx)^2)/x)||συν(1/x)|=[(((ημx)^2)/|x|]|συν(1/x)|<=(((ημx)^2)/|x|
Επομένως
-(((ημx)^2)/|x|)<=(((ημx)^2)/x)συν(1/x)<=((ημx)^2)/|x| για κάθε x ανήκει R*
Αν x>0 τότε |x|=x, οπότε ισχύει -(((ημx)^2)/x)<=(((ημx)^2)/x)συν(1/x)<=((ημx)^2)/x για κάθε x ανήκει (0,+οο)
lim(x->0+)[-(((ημx)^2)/x)]=-lim(x->0+)(((ημx)^2)/x)=-0=0
Επειδή lim(x->0+)[-(((ημx)^2)/x)]=lim(x->0+)(((ημx)^2)/x)=0 τότε σύμφωνα με το κριτήριο παρεμβολής lim(x->0+)[(((ημx)^2)/x)συν(1/x)]=0
Αν x<0 τότε |x|=-x, οπότε ισχύει ((ημx)^2)/x<=(((ημx)^2)/x)συν(1/x)<=-(((ημx)^2)/x) για κάθε x ανήκει (-oo,0)
lim(x->0-)[-(((ημx)^2)/x)]=-lim(x->0-)(((ημx)^2)/x)=-0=0
Επειδή lim(x->0-)(((ημx)^2)/x)=lim(x->0-)[-(((ημx)^2)/x)]=0 τότε σύμφωνα με το κριτήριο παρεμβολής lim(x->0-)[(((ημx)^2)/x)συν(1/x)]=0
Επειδή lim(x->0-)[(((ημx)^2)/x)συν(1/x)]=lim(x->0+)[(((ημx)^2)/x)συν(1/x)]=0 τότε lim(x->0)[(((ημx)^2)/x)συν(1/x)]=0
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.



Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Επειδή
Επίσης
οπότε
Λόγω του κριτηρίου παρεμβολής τελικά το όριο είναι 0.
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


Λίγο πιο σύντομα η λύση του Γιώργου:
Επειδήείναι
Επίσης
οπότε
Λόγω του κριτηρίου παρεμβολής τελικά το όριο είναι 0.
στη δευτερη γραμμη γτ να ειναι μικροτερο η ισο αυτου του απολυτου;; του |ημ²χ/χ| ?
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 0 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 231 μέλη διάβασαν αυτό το θέμα:
- ChrisG152
- giorgos5002
- giannis06
- Panagiwths12
- mikke
- hristosdab
- trifasikodiavasma
- haji
- thepigod762
- Mariosm.
- soulatso
- oteletampis
- phleidhs
- AggelikiGr
- sir ImPeCaBlE
- veiNqh
- Scandal
- alekos
- Debugging_Daemon
- just some guy
- xristosgkm
- ismember
- Apocalypse
- arrow25
- rempelos42
- ggl
- GStef
- QWERTY23
- xrisamikol
- Σωτηρία
- nikoletaz57
- _Aggelos123
- Mariam38
- SlimShady
- strsismos88
- Georgekk
- Lia 2006
- igeorgeoikonomo
- marian
- tsiobieman
- constansn
- Xristosdimitra
- Panagiotis849
- ρενακι 13
- Memetchi
- eukleidhs1821
- Nikkkpat
- Unboxholics
- korlef
- kwstaseL
- Thanos_D
- the purge
- T C
- Giii
- Papachrist
- liaiscool
- Αννα Τσιτα
- globglogabgalab
- Pharmacist01
- otinanai123
- abcdefg12345
- nicole1982
- thecrazycretan
- kvstas92
- KingOfPop
- maria301
- papa2g
- stefan
- Κλημεντίνη
- TonyMontanaEse
- Lathy
- Alexecon1991
- Μάρκος Βασίλης
- Cortes
- το κοριτσι του μαη
- calliope
- ale
- panagiotis G
- Kleanth
- aggelosst9
- BioChemical
- spring day
- nucomer
- Georgia110
- LeoDel
- pink_panther
- Alexandros973
- marsenis
- den antexw allh apotyxia
- KaterinaL
- kiyoshi
- drosos
- Λαμπρινηη
- Bill22
- Chrysablac.
- giorgosp97
- Βλα
- Monster Hunter
- jul25
- xxxtolis
- Stroka
- nicks1999
- totiloz
- Earendil
- mitsakos
- tasost
- lnesb
- ssalex
- alan09
- Livaja10
- χημεια4λαιφ
- Viedo
- UncleJ
- Kostakis45
- Infrared
- Zgian
- pepatogourounaki
- hirasawayui
- GeoCommand
- Eleni54
- American Economist
- EiriniS20
- ΘανάσοςG4
- stamoul1s
- Αριάνα123
- uni77
- Libertus
- tasoss
- PanosCh002
- Unseen skygge
- Νικόλας Ραπ.
- cel123
- The Limit Does Not Exist
- don_vito
- suaimhneas
- Αλκης Κ.
- alexrami
- Baggelitsa36
- Νομικάριος13
- spinalgr1990
- d_th
- Adolfo valencia
- Πα.Κ
- Vasilis25
- Johnman97
- Steffie88
- rekcoR
- gwgw_5
- fockos
- Mariahj
- roud
- kostas83
- Cpt.Philips
- Makis45
- Χρησλου
- Panos_02
- Vold
- tymvorixos
- GiorgosAsi
- Neos167
- theodoraooo
- George187
- Άρτεμις Α.
- Μαρία2222
- christos87
- Idontknoww
- jimis2001
- Metamorph
- Γατόπαρδος.
- Johnsk
- mitsos14
- johnsiak
- Elel
- Dreamer_SW
- Γιαννης1987Θεσσ
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki



