

Μόνο το δύο πολ/ζεται με την δεύτερη ρίζα ή το x-2.
?
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


ποιος ειναι ο συζυγης του;
Γιατί δεν δοκιμάζεις να πολλαπλασιάσεις με την συζυγή παράσταση αριθμητή και παρονομαστή να δεις τι θα προκύψει;Αυτός
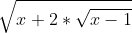
Προσπάθησε να εξαφανίσεις τα απόλυτα βλέποντας τι πρόσημο έχουν οι παραστάσεις που περικλείουν κοντά στο 0. Προσπάθησε να σκεφτείς ένα παράδειγμα "πολυωνυμικής περιττής συνάρτησης" για να δεις ότι όποια κι αν είναι αυτή, τοΓειά σας!Μπορείτε να με βοηθήσετε στην άσκηση 34, σελ. 177, τεύχος Α του Μπάρλα?Η άσκηση λέει: Έστω η πολυωνυμική περιττή συνάρτηση P(x).Να βρείτε το όριο: lim(x->0) του (|P(x)ημ(χ) +1| - |xP(-x)+1|)/x
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
chester20080
Επιφανές μέλος


Προσπάθησε να εξαφανίσεις τα απόλυτα βλέποντας τι πρόσημο έχουν οι παραστάσεις που περικλείουν κοντά στο 0. Προσπάθησε να σκεφτείς ένα παράδειγμα "πολυωνυμικής περιττής συνάρτησης" για να δεις ότι κι αν είναι αυτή, τοδεν λέω άλλα.
Οκ,ευχαριστώ,το έβγαλα...
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


το βρηκα! ευχαριστω

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
JKaradakov
Τιμώμενο Μέλος


Για πείτε τι να κάνω;
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
vimaproto
Πολύ δραστήριο μέλος


Για πείτε τι να κάνω;
Ονομάζω Ζ=x+yi
Το αριστερό μέρος είναι
Δεν ξέρω αν είναι ευφυής η λύση αλλά είναι λύση.
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lowbaper92
Πολύ δραστήριο μέλος


Για πείτε τι να κάνω;
Το πρώτο δεδομένο δε χρειάζεται.
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
JKaradakov
Τιμώμενο Μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
JKaradakov
Τιμώμενο Μέλος


Είπα:
Αφού
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
*Serena*
Τιμώμενο Μέλος


2) Εστω f(z)= iz-2+4i/ z-i. Να βρείτε την καμπύλη στην οποία ανήκουν τα σημεία Μ(ζ) αν f(z) ανήκει R.
3) Αν w=f(z)-i να υπολιγίσετε τον αριθμό [ριζα 2/3 * w] ^2010
Βοηθεια?

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
mary-blackrose
Εκκολαπτόμενο μέλος


ασκηση 32 σελ 231 μπαρλας ..
δινεται η συναρτηση [LATEX]\lim _{ x\rightarrow 0 }{ \frac { f\left( x \right) +1+\eta \mu \chi }{ { x }^{ 2 }+x } } =\lambda [/LATEX] και Α(0,-1) ε Cf.
i)δ.ο. η f συνεχησ στο χο=0
ii)Aν[LATEX]\lim _{ x\rightarrow 0 }{ \frac { f\left( x \right) +1 }{ \eta \mu \chi } } =3[/LATEX] να βρειτε το λ.
ασκηση 9 σελ 228 μπαρλας βρειτε το λ ωστε f συνεχης στο χο=0:
[LATEX]f\left( x \right) =\begin{ cases } \frac { \sqrt { { x }^{ 4 }+{ x }^{ 2 } } +\eta \mu 2\chi }{ { x }^{ 2 }+x } \quad x>0 \\ { \quad \quad \quad \quad \quad e }^{ x }+\lambda \quad \quad \quad \quad \quad \quad x\le 0 \end{ cases }[/LATEX]Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Kαι γιατί δεν μπορεί να είναιΕφραψα σήμερα ένα διαγώνισμα και θέλω την γνώμη σας σε ένα ερώτημα που νομίζω ότι έκανα πατάτα.
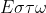
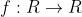
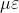
\neq 0, )
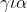
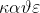
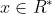
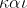
)=xf(x),)
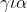
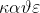
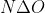
Είπα:
Αφούγια κάθε xεR*, άρα η f(x) έχει μία ρίζα η οποία είναι η x=0 άρα f(0)=0
Πάντως έχω την εντύπωση ότι βγαίνει και μόνο με την χρήση της σχέσης f(f(x))=xf(x)
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lowbaper92
Πολύ δραστήριο μέλος


Εφραψα σήμερα ένα διαγώνισμα και θέλω την γνώμη σας σε ένα ερώτημα που νομίζω ότι έκανα πατάτα.
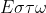
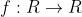
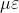
\neq 0, )
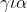
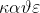
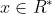
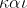
)=xf(x),)
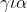
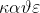
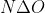
Είπα:
Αφούγια κάθε xεR*, άρα η f(x) έχει μία ρίζα η οποία είναι η x=0 άρα f(0)=0
Διαφορετικά
Για x=0 στην αρχική:
Για x=f(0) στην αρχική:
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
JKaradakov
Τιμώμενο Μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Aris90
Εκκολαπτόμενο μέλος
JKaradakov
Τιμώμενο Μέλος


Μου δίνει την σχέση
a)να βρω τον γτ. (Των έχω βρει)
β)την ελάχιστη τιμή του
Πως το βρίσκω το β;
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


i)μια βοηθεια στις παρακατω ασκησεις....
ασκηση 32 σελ 231 μπαρλας ..Code:δινεται η συναρτηση [LATEX]\lim _{ x\rightarrow 0 }{ \frac { f\left( x \right) +1+\eta \mu \chi }{ { x }^{ 2 }+x } } =\lambda [/LATEX] και Α(0,-1) ε Cf. i)δ.ο. η f συνεχησ στο χο=0 ii)Aν[LATEX]\lim _{ x\rightarrow 0 }{ \frac { f\left( x \right) +1 }{ \eta \mu \chi } } =3[/LATEX] να βρειτε το λ. ασκηση 9 σελ 228 μπαρλας βρειτε το λ ωστε f συνεχης στο χο=0: [LATEX]f\left( x \right) =\begin{ cases } \frac { \sqrt { { x }^{ 4 }+{ x }^{ 2 } } +\eta \mu 2\chi }{ { x }^{ 2 }+x } \quad x>0 \\ { \quad \quad \quad \quad \quad e }^{ x }+\lambda \quad \quad \quad \quad \quad \quad x\le 0 \end{ cases }[/LATEX]
α) Θέτεις
(έχει ο Μπάρλας παρόμοιες λυμένες)
β)
Είναι
Θυμίσου από πέρυσι την απόσταση σημείου από ευθεία.Παιδιά έχω μια ξανθιά στιγμή οπότε λίγο βοήθεια.
Μου δίνει την σχέση
a)να βρω τον γτ. (Των έχω βρει)
β)την ελάχιστη τιμή του
Πως το βρίσκω το β;
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
JKaradakov
Τιμώμενο Μέλος


i)
α) Θέτεις
(έχει ο Μπάρλας παρόμοιες λυμένες)
β)
Είναι
Θυμίσου από πέρυσι την απόσταση σημείου από ευθεία.
Got it!

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
kwstas211t
Νεοφερμένο μέλος


(απαντηση για το β 'ιορδανη')
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
*Serena*
Τιμώμενο Μέλος


Κάποιος?1) Αν ζ=5+3ριζα 3*i /1-2ριζα3*i να αποδείξετε ότι ζ^3 Ε R.
2) Εστω f(z)= iz-2+4i/ z-i. Να βρείτε την καμπύλη στην οποία ανήκουν τα σημεία Μ(ζ) αν f(z) ανήκει R.
3) Αν w=f(z)-i να υπολιγίσετε τον αριθμό [ριζα 2/3 * w] ^2010
Βοηθεια?

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 2 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 232 μέλη διάβασαν αυτό το θέμα:
- Hased Babis
- ChrisG152
- giorgos5002
- giannis06
- Panagiwths12
- mikke
- hristosdab
- trifasikodiavasma
- haji
- thepigod762
- Mariosm.
- soulatso
- oteletampis
- phleidhs
- AggelikiGr
- sir ImPeCaBlE
- veiNqh
- Scandal
- alekos
- Debugging_Daemon
- just some guy
- xristosgkm
- ismember
- Apocalypse
- arrow25
- rempelos42
- ggl
- GStef
- QWERTY23
- xrisamikol
- Σωτηρία
- nikoletaz57
- _Aggelos123
- Mariam38
- SlimShady
- strsismos88
- Georgekk
- Lia 2006
- igeorgeoikonomo
- marian
- tsiobieman
- constansn
- Xristosdimitra
- Panagiotis849
- ρενακι 13
- Memetchi
- eukleidhs1821
- Nikkkpat
- Unboxholics
- korlef
- kwstaseL
- Thanos_D
- the purge
- T C
- Giii
- Papachrist
- liaiscool
- Αννα Τσιτα
- globglogabgalab
- Pharmacist01
- otinanai123
- abcdefg12345
- nicole1982
- thecrazycretan
- kvstas92
- KingOfPop
- maria301
- papa2g
- stefan
- Κλημεντίνη
- TonyMontanaEse
- Lathy
- Alexecon1991
- Μάρκος Βασίλης
- Cortes
- το κοριτσι του μαη
- calliope
- ale
- panagiotis G
- Kleanth
- aggelosst9
- BioChemical
- spring day
- nucomer
- Georgia110
- LeoDel
- pink_panther
- Alexandros973
- marsenis
- den antexw allh apotyxia
- KaterinaL
- kiyoshi
- drosos
- Λαμπρινηη
- Bill22
- Chrysablac.
- giorgosp97
- Βλα
- Monster Hunter
- jul25
- xxxtolis
- Stroka
- nicks1999
- totiloz
- Earendil
- mitsakos
- tasost
- lnesb
- ssalex
- alan09
- Livaja10
- χημεια4λαιφ
- Viedo
- UncleJ
- Kostakis45
- Infrared
- Zgian
- pepatogourounaki
- hirasawayui
- GeoCommand
- Eleni54
- American Economist
- EiriniS20
- ΘανάσοςG4
- stamoul1s
- Αριάνα123
- uni77
- Libertus
- tasoss
- PanosCh002
- Unseen skygge
- Νικόλας Ραπ.
- cel123
- The Limit Does Not Exist
- don_vito
- suaimhneas
- Αλκης Κ.
- alexrami
- Baggelitsa36
- Νομικάριος13
- spinalgr1990
- d_th
- Adolfo valencia
- Πα.Κ
- Vasilis25
- Johnman97
- Steffie88
- rekcoR
- gwgw_5
- fockos
- Mariahj
- roud
- kostas83
- Cpt.Philips
- Makis45
- Χρησλου
- Panos_02
- Vold
- tymvorixos
- GiorgosAsi
- Neos167
- theodoraooo
- George187
- Άρτεμις Α.
- Μαρία2222
- christos87
- Idontknoww
- jimis2001
- Metamorph
- Γατόπαρδος.
- Johnsk
- mitsos14
- johnsiak
- Elel
- Dreamer_SW
- Γιαννης1987Θεσσ
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki




