Βοήθεια/Aπορίες στα Μαθηματικά Προσανατολισμού

[coheNakatos]

Φίλοι του φόρουμ εχω μια ασκηση στην οποία ζητάω βοήθεια, παρακαλώ βοηθήστε με. η ασκηση είναι: Να αποδειχθεί οτι για κάθε πραγματικο αριθμό α υπάρχει μοναδικός θετικός αριθμος β τέτοιος ώστε να ισχύει: α= -1/β^3 + lnβ

Θεωρω την συναρτηση

Παιρνεις ορια στο και ( προσεξε σε ποιο διαστημα θα εφαρμοσεις bolzano ) ->εδειξες οτι υπαρχει τουλαχιστον 1 ριζα

Και δειχνοντας οτι ειναι και γν μονοτονη θα εχεις και μοναδικη ριζα ->μοναδικο b

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Alibaba]

Ευχαριστώ φίλε Βαγγέλη! μηπώς μπορείτε να με διαφωτίσετε και για μια αλλη άσκηση? Ασκηση:
Έστω οι συνεχείς συναρτήσεις f, g: [α,β] --> R και μια τυχαια ευθεία (ε): χ=t που τέμνει τις Cf και Cg στα σημεία Α και Β αντίστοιχα. Να δειχθεί ότι υπάρχει ευθεία (ε), ώστε η απόσταση ΑΒ να είναι η μεγαλύτερη.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[manos66]

Ευχαριστώ φίλε Βαγγέλη! μηπώς μπορείτε να με διαφωτίσετε και για μια αλλη άσκηση? Ασκηση:
Έστω οι συνεχείς συναρτήσεις f, g: [α,β] --> Rκαι μια τυχαια ευθεία (ε): χ=t που τέμνει τις Cfκαι Cgστα σημεία Α και Β αντίστοιχα. Να δειχθεί ότι υπάρχει ευθεία (ε), ώστε η απόσταση ΑΒ να είναι η μεγαλύτερη.

H απόσταση ΑΒ είναι η κατακόρυφη απόσταση των Cf, Cg.
AB = | f (x) - g (x) | = h (x)
H h είναι συνεχής στο [α , β].
Θεώρημα μέγιστης-ελάχιστης τιμής
...

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Alibaba]

ευχαριστω! μπορεις να μου εξηγήσεις και μετα πως το λύνω με το θεώρημα μεγιστης και ελαχιστης τιμής?

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[manos66]

ευχαριστω! μπορεις να μου εξηγήσεις και μετα πως το λύνω με το θεώρημα μεγιστης και ελαχιστης τιμής?

Το θ. μέγιστης-ελάχιστης τιμής μου δίνει ότι η συνεχής h παρουσιάζει μέγιστο στο [α , β].
Αυτό ζητάει η άσκηση.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[ledzeppelinick]

Γιατι αφήνεις μόνο το μεγιστοβάθμιο όρο του κάθε πολυωνύμου; είναι ιδιότητα or what?

Όταν έχεις όριο στο άπειρο σε μια ρητή συναρτηση αρκέι να πάρεις μόνο το όριο του λόγου των μεγοστοβάθμιων όρων!

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[πηνελοπη41056]

παιδια εχω απελπιστει..αν καποιος μπορει να με βοηθησει λιγο η εστω να μ δειξει μια υποδειξη θα το εκτιμουσα..
Δινονται οι μιγαδικοι z και με , z,w φανταστικοι
θεωρουμε τη συνεχη στο διαστημα [α,β] πραγματικη συναρτηση f με με f(α)>1 (f(x) R για καθε x [α,β]
Αν z=f(α)i και w=f(β)i , τοτε να δειξετε οτι η εξισωση f(x)=0 εχει μια τουλαχιστον ριζα στο (α,β)


ευχαριστω

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[coheNakatos]

παιδια εχω απελπιστει..αν καποιος μπορει να με βοηθησει λιγο η εστω να μ δειξει μια υποδειξη θα το εκτιμουσα..
Δινονται οι μιγαδικοι z και με , z,w φανταστικοι
θεωρουμε τη συνεχη στο διαστημα [α,β] πραγματικη συναρτηση f με με f(α)<1 (f(x) R για καθε x [α,β]
Αν z=f(α)i και w=f(β)i , τοτε να δειξετε οτι η εξισωση f(x)=0 εχει μια τουλαχιστον ριζα στο (α,β)


ευχαριστω

πρεπει να εχεις κανει λαθος ενα προσημο αν δεν κανω λαθος

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[πηνελοπη41056]

το διορθωσα...ειναι f(α)>1
μηπως εχεις καμια ιδεα?

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[coheNakatos]

το διορθωσα...ειναι f(α)>1
μηπως εχεις καμια ιδεα?

Αντικαθιστω στην δοθεισα σχεση και εχω

Και φυσικα αρα απο την

οκ ?

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[πηνελοπη41056]

ok!!ευχαριστω πολυ!!ειλικρινα ωρες ωρες νιωθω χαζη

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[angelica_pickles]

Αν f,g συναρτησεις συνεχεις στο R με
και και
να δειξετε οτι υπαρχει ενα τουλαχιστον τετοιο ωστε


παιδια ελπιζω καποιος να μπορει να βοηθησει!!!100 ωρες εγραφα!
ευχαριστω

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[manos66]

Αν f,g συναρτησεις συνεχεις στο R με
και και
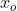
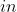
να δειξετε οτι υπαρχει ενα τουλαχιστον τετοιο ωστε


παιδια ελπιζω καποιος να μπορει να βοηθησει!!!100 ωρες εγραφα!
ευχαριστω

Από τα όρια και τη συνέχεια των f,g προκύπτει ότι f (2) = 1 και g (2) = 1/2.

θεωρούμε τη συνάρτηση h με
Η h είναι συνεχής στο [2 , 3] ως πράξεις συνεχών
h(2) = - g(2) = -1/2 < 0
*
Θ. Bolzano ...

* Έστω συνάρτηση φ (x) = f (x) - g (x)
Η φ είναι συνεχής ως διαφορά συνεχών και δεν έχει ρίζες, άρα από συνέπειες του Θ. Bolzano διατηρεί σταθερό πρόσημο στο R.
φ(2) = f (2) - g (2) = 1 - 1/2 = 1/2 > 0,
άρα φ (x) > 0, για κάθε x πραγματικό.
φ (3) = f (3) - g (3) > 0

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[asap]

Εχω φάει κόλλημα σε αυτες τις δυο

1.Να δείξετε οτι οι γραφικές παραστάσεις των συναρτήσεων f(x)=1/x και g(x)=(x^2)-x+1 έχουν ενα κοινό σημείο στο οποιο οι εφαπτομένες τους είναι κάθετες

2.Δίνονται οι συναρτήσεις f(x)=e^χ και g(x)=(-x^2)-x Να δείξετε οτι η εφαπτομένη της Cf στο σημείο Α(0,1) εφάπτεται και στην Cg

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Rania.]

Ε για το 1 θα κανεις f(x)=g(x) και θα βρεις το σημειο στο οποιο ισχυει f'(x)g'(x)=-1

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[dannaros]

ε και στο δεύτερο βρίσκεις την εφαπτομένη της Cf στο Α και αρκεί να δείξεις ότι το λ της εφαπτομένης ισούται με το g'(του κοινού τους σημείου)

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Avatar]

Παιδια εχω προβλημα με ενα συγκεκριμενο τυπο ασκησεων στις παραγωγους.Δειτε:

Αν fR->R ειναι παραγωγισιμη στο Χο=0 με f '(0)=aεR και f(x+y)=f(x)f(y) για καθε χ,yεR me f(0) διαφορο του μηδεν να δειχθει οτι η f ειναι παραγωγισιμη στο R.
--------------------
Αλλη

Δινεται η συναρτηση f με f(xy)=f(x)f(y) για καθε χ,yεR με f(x) διαφορο του μηδεν.Αν η συναρτηση f ειναι παραγωγισιμη στο Χο=1 να δειχθει οτι ειναι παραγωγισιμη σε καθε ΧοεR εκτος του μηδεν.

Ευχαριστω!

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[metalmaniac]

ΑΣΚΗΣΗ

να βρείτε τα σημεία της γραφικής παραστασης της συνάρτησης f(x)=ημ2χ-2ημ^2)χ ,χ ανήκει στο [0,2π] στα οποία η εφαπτομένη της είναι παράλληλη στον χ'χ

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[coheNakatos]

Παιδια εχω προβλημα με ενα συγκεκριμενο τυπο ασκησεων στις παραγωγους.Δειτε:

Αν fR->R ειναι παραγωγισιμη στο Χο=0 με f '(0)=aεR και f(x+y)=f(x)f(y) για καθε χ,yεR me f(0) διαφορο του μηδεν να δειχθει οτι η f ειναι παραγωγισιμη στο R.
--------------------
Αλλη

Δινεται η συναρτηση f με f(xy)=f(x)f(y) για καθε χ,yεR με f(x) διαφορο του μηδεν.Αν η συναρτηση f ειναι παραγωγισιμη στο Χο=1 να δειχθει οτι ειναι παραγωγισιμη σε καθε ΧοεR εκτος του μηδεν.

Ευχαριστω!

Πας με ορισμο , παιρνεις τυχαιο και προσπαθεις να δειξεις οτι το οριο ανηκει στο R (εχε στο νου σου το δεδομενο στοχευσε το,δηλ προσπαθησε να το εμφανισεις γιατι ξερεις οτι ανηκει στο R ).Επισης το οτι θα πας με ορισμο στο δειχνει η εκφωνηση και το ζητουμενο ,Θελεις να δειξεις οτι ειναι παραγωγισιμη γιαυτο δεν παραγωγιζεις κατα μελη
-----------------------------------------

ΑΣΚΗΣΗ

να βρείτε τα σημεία της γραφικής παραστασης της συνάρτησης f(x)=ημ2χ-2ημ^2)χ ,χ ανήκει στο [0,2π] στα οποία η εφαπτομένη της είναι παράλληλη στον χ'χ

βρες την παραγωγο και λες οτι πρεπει και λυνεις την εξισωση (θυμισου τα περσινα εχεις συγκεκριμενο διαστημα το [0,2π] εκει να περιορισεις τις λυσεις σου) .

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[stratos_man]

Πας με ορισμο , παιρνεις τυχαιο και προσπαθεις να δειξεις οτι το οριο ανηκει στο R (εχε στο νου σου το δεδομενο στοχευσε το,δηλ προσπαθησε να το εμφανισεις γιατι ξερεις οτι ανηκει στο R ).Επισης το οτι θα πας με ορισμο στο δειχνει η εκφωνηση και το ζητουμενο ,Θελεις να δειξεις οτι ειναι παραγωγισιμη γιαυτο δεν παραγωγιζεις κατα μελη
-----------------------------------------


βρες την παραγωγο και λες οτι πρεπει και λυνεις την εξισωση (θυμισου τα περσινα εχεις συγκεκριμενο διαστημα το [0,2π] εκει να περιορισεις τις λυσεις σου) .

Ρε Βαγγελη να σε ρωτησω κατι..σχολειο δεν πας.??? συνηθως εγω στις 9 ειμαι στο σχολειο...

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.