
10-02-15

12:35
Καλημέρα, είμαι φοιτήτρια εφαρμοσμένης πληροφορικής στην Ιταλία, δυστυχώς στο λύκειο ήμουν στην θεωρητική και έχω απίστευτα κενά στα μαθηματικά και τώρα δυσκολεύομαι, υπάρχει κάποιος που μπορεί να μου λύσει αυτή την άσκηση αναλυτικά για να καταλάβω τη μέθοδο και να μπορέσω να λύσω και τις υπόλοιπες παρόμοιες; Ευχαριστώ εκ των προτέρων.
*Η άσκηση
Να βρεθεί η μέγιστη τιμή και το διπλό ολοκλήρωμα της συνάρτησης: f(x,y)= y^2 -y√x + x^2
σε πεδίο του καρτεσιανού επιπέδου ορισμένο από τις ανισώσεις: 1/2 ≤ x ≤ 1, 0 ≤ y ≤ √x
*Η άσκηση
Να βρεθεί η μέγιστη τιμή και το διπλό ολοκλήρωμα της συνάρτησης: f(x,y)= y^2 -y√x + x^2
σε πεδίο του καρτεσιανού επιπέδου ορισμένο από τις ανισώσεις: 1/2 ≤ x ≤ 1, 0 ≤ y ≤ √x
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος
Ο Κώστας αυτή τη στιγμή δεν είναι συνδεδεμένος. Μας γράφει από Ηράκλειο (Αττική). Έχει γράψει 1.025 μηνύματα.

11-02-15

03:09
Καλημέρα, είμαι φοιτήτρια εφαρμοσμένης πληροφορικής στην Ιταλία, δυστυχώς στο λύκειο ήμουν στην θεωρητική και έχω απίστευτα κενά στα μαθηματικά και τώρα δυσκολεύομαι, υπάρχει κάποιος που μπορεί να μου λύσει αυτή την άσκηση αναλυτικά για να καταλάβω τη μέθοδο και να μπορέσω να λύσω και τις υπόλοιπες παρόμοιες; Ευχαριστώ εκ των προτέρων.
*Η άσκηση
Να βρεθεί η μέγιστη τιμή και το διπλό ολοκλήρωμα της συνάρτησης: f(x,y)= y^2 -y√x + x^2
σε πεδίο του καρτεσιανού επιπέδου ορισμένο από τις ανισώσεις: 1/2 ≤ x ≤ 1, 0 ≤ y ≤ √x
Για την μέγιστη τιμή ακολουθώντας τον τρόπο που αναφέρεται στο παράδειγμα εδώ σελ 30...
Η συνάρτηση

Ι) Κρίσιμα σημεία (εσωτερικά σημεία της f στο χωρίο ΑΒΓΔ, που οι μερικές παράγωγοι μηδενίζονται)
ΙΙ) Συνοριακά σημεία - που βρίσκονται πάνω στα τμήματα ΑΒ,ΒΓ,ΓΔ,ΔΑ. Υπολογίζω το μέγιστο και το ελάχιστο της f σε καθένα απ' αυτά τα τμήματα.
Στο τέλος συγκρίνω τις τιμές της f στα σημεία Ι) και ΙΙ) και επιλέγω την μέγιστη ( αν ήθελα την ελάχιστη τιμή της f θα επέλεγα την ελάχιστη απ' τις παραπάνω τιμές). Εκεί η f παρουσιάζει μέγιστο.
Ι) Οι μερικές παράγωγοι ( κρατάω τη μία μεταβλητή σταθερή και παραγωγίζω ως προς την άλλη μεταβλητή) είναι
προκύπτει
II) Στο τμήμα ΑΒ είναι
Στο τμήμα ΒΓ είναι
Στο τμήμα ΓΔ είναι
Στο τμήμα ΑΔ είναι
Από τις τιμές (1) έως ( 8 ) της f επιλέγω την μεγαλύτερη. Έτσι παρατηρούμε ότι το μέγιστο της f στο χωρίο ΑΒΓΔ είναι
Η συνάρτηση γράφεται
οπότε
Η ισότητα επιτυγχάνεται για
Τα παραπάνω ίσως φαίνονται δύσκολα αλλά είναι επέκταση της αντίστοιχης μεθοδολογίας εύρεσης μεγίστων και ελαχίστων για συναρτήσεις μίας μεταβλητής. Επομένως θα σε συμβούλευα κατ' αρχάς να διαβάσεις ότι χρειάζεται από δω, ενδεχομένως και προηγούμενα κεφάλαια. Αυτά βρίσκουν εφαρμογή και στην συγκεκριμένη άσκηση γιατί σε κάθε περίπτωση ανάγεσαι σε συναρτήσεις μίας μεταβλητής (πχ το ελάχιστο και το μέγιστο του τριωνύμου
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
eyb0ss
Δραστήριο μέλος
Ο eyb0ss αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Φοιτητής και μας γράφει από Αθήνα (Αττική). Έχει γράψει 742 μηνύματα.

11-02-15

03:56
Το ζητούμενο ολοκλήρωμα είναι το dydx)
Υπολογίζουμε πρώτα το εσωτερικό ολοκλήρωμα:
dy=\int_0^{\sqrt{x}}(y^2-yx^{1/2}+x^2)dy=\int_0^{\sqrt{x}}y^2dy-x^{1/2}\int_0^{\sqrt{x}}ydy+x^2\int_0^{\sqrt{x}}1dy=\frac{x^{3/2}}{3}-\frac{x^{3/2}}{2}+x^{5/2}=-\frac{x^{3/2}}{6}+x^{5/2})
Άρα αρκεί να βρούμε το ολοκλήρωμαdx)
dx=-\frac{1}{6}\int_{1/2}^1x^{3/2}dx+\int_{1/2}^1x^{5/2}dx=-\frac{1}{6}\int_{1/2}^1\left(\frac{2x^{5/2}}{5}\right)'dx+\int_{1/2}^1\left(\frac{2x^{7/2}}{7}\right)'dx=\frac{1-2\sqrt{2}}{30\sqrt{2}}+\frac{8\sqrt{2}-1}{28\sqrt{2}}\approx 0,206)
Άρα
dydx\approx 0,206)
Ιδιότητες που χρησιμοποιήθηκαν:
1) Μια παράγουσα της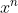 είναι η
είναι η 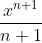 με
με 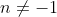
2) Αν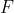 μια παράγουσα της
μια παράγουσα της 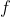 (δηλαδή ισχύει ότι
(δηλαδή ισχύει ότι 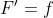 ) τότε
) τότε dx=F(b)-F(a))
3)+\lambda g(x)\right)dx=\kappa\int_a^bf(x)dx+\lambda\int_a^bg(x)dx)
Υπολογίζουμε πρώτα το εσωτερικό ολοκλήρωμα:
Άρα αρκεί να βρούμε το ολοκλήρωμα
Άρα
Ιδιότητες που χρησιμοποιήθηκαν:
1) Μια παράγουσα της
2) Αν
3)
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

11-02-15

10:30
Χίλια ευχαριστώ παιδιά, με σώζετε! 

Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 1 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 3 μέλη διάβασαν αυτό το θέμα:
-
Φορτώνει...
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki



