Η ταχύτητα ενός σώματος έχει πεπερασμένο μέτρο καθώς αν είχε την δυνατότητα να τείνει στο άπειρο τότε θα γινόταν μεγαλύτερη από την ταχύτητα του φωτός, που δεν μπορεί να συμβεί.
Αν ένα σώμα με μάζα
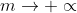
μετακινείται με ταχύτητα υ η οποία είναι πεπερασμένη όπως αποδείχτηκε τότε η κινητική του ενέργεια
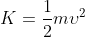
θα έτεινε στο άπειρο
=\lim_{m\rightarrow +\propto }\left( \frac{1}{2}m{\upsilon }^{2}\right)=+\propto )
, κάτι που δεν μπορεί να συμβεί. Άρα ένα σώμα με μάζα
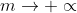
δεν μπορεί να μετακινηθεί, δηλαδή υ=0.
Συνεπώς αφού για ένα σώμα άπειρης μάζας είναι υ=0 σε κάθε χρονική στιγμή, τότε θα είναι
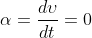
σε κάθε χρονική στιγμή και επόμενως η συνισταμένη δύναμη που ασκείται σε αυτό θα είναι F=0, δηλαδή δεν ασκείται σε αυτό καμία δύναμη εφόσον ισορροπεί.
Συνεπώς ένα σώμα άπειρης μάζας δεν μπορεί να μετακινηθεί αλλά παραμένει συνεχώς στην ίδια θέση και δεν είναι δυνατόν να ασκηθεί καμία δύναμη (ή ροπή αν πρόκειται για στερεό σώμα) σε αυτό.
Συνεπώς δύναμη μέτρου
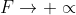
μπορεί να εφαρμοστεί μόνο σε σώμα πεπερασμένης μάζας στο οποίο ισχύει
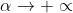
. Όμως το μέτρο της επιτάχυνσης ως ρυθμού μεταβολής της ταχύτητας και κλίσης του διαγράμματος υ-t δεν μπορεί να τείνει στο άπειρο σε χρονικό διάστημα παρά μόνο σε μεμονωμένες χρονικές στιγμές. Σε αυτές τις χρονικές στιγμές η συνισταμένη δύναμη F έχει μέτρο
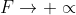
.
Επίσης ένα σώμα άπειρης μάζας δεν μπορεί να περικλείει άπειρη ποσότητα δυναμικής ενέργειας λόγω της παρουσίας του σε βαρυτικό πεδίο πεπερασμένης έντασης καθώς η συνισταμένη δύναμη που ασκείται σε αυτό είναι μηδέν και έτσι δεν μπορεί να υφίσταται την επίδραση μόνο του βαρυτικού πεδίου. Όμως σύμφωνα με την σχέση της βαρυτικής δυναμικής ενέργειας U=(GMm)/r, όπου M πεπερασμένο, για να είναι lim(m->+άπειρο)U=U0 πρέπει lim(m->+άπειρο)r=+άπειρο που σημαίνει ότι το σώμα άπειρης μάζας βρίσκεται σε άπειρη απόσταση από την πηγή M του βαρυτικού πεδίου. Η σταθερά U0 είναι πραγματικός αριθμός (εφόσον το όριο υπάρχει και είναι πραγματικός ατιθμός) και δεν μπορεί να προσδιοριοστεί παρά μόνο αν ξέρουμε συναρτήσεις m=f(u) και r=g(u) όπου για κάποια τιμή u0 (πεπερασμένη ή +- άπειρο) ισχύει lim(u->u0)f(u)=lim(u->u0)g(u)=+ άπειρο και lim(u->u0)[(G/M)*(f(u)/g(u))]=U0 ανήκει R, τουλάχιστον για κάποιο από τα δύο πλευρικά όρια. Τότε το U0 μπορεί να υπολογιστεί (εφόσον υπάρχει φυσικά).
Συνεπώς ένα σώμα άπειρης μάζας θα βρίσκεται υποχρεωτικά σε άπειρη απόσταση από την πηγή του βαρυτικού πεδίου. Δεν γίνεται να δέχεται την επίδραση του γιατί τότε το r θα ήταν πεπερασμένο και η δυναμική ενέργεια άπειρη. Παρ' όλα αυτά η δυναμική του ενέργεια δεν θα είναι απαραίτητα 0 αλλά μπορεί να είναι οποιοσδήποτε πραγματικός αριθμός.
Έτσι ικανοποιούνται οι νόμοι πεπερασμένης ταχύτητας και ενέργειας.