vimaproto
Πολύ δραστήριο μέλος


1)logx=2/3=log10^(2/3) ==> x=2/3μπορει να βοηθησει κανεις στις παρακατω ασκησεις...??
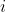3logx-2=0<br />
ii)2{ log }^{ 2 }x-3logx=0<br />
iii){ 2 }^{ x }=3<br />
iv){ 3 }^{ x }+{ 3 }^{ x+1 }+{ 3 }^{ x-1 }=26<br />
v)ln({ e }^{ 2x }+2)=x) Code:
Code:
....καθε υποδειξη ευπροσδεκτη..
2) κοινός παράγοντας ο logx και logx=0=log1 ==> x=1 ή logx=3/2=log10^(3/2) ==>x=10^(3/2) ή 10ρίζα10
3) λογαριθμίζω τα δύο μέλη χlog2=log3 ==> x=log3/log2
4) Ονομάζω 3^χ=y. Η εξίσωση γράφεται y+3y+y/3=26 ==>13y=3.26 ==> y=6 και 3^χ=6 και λογαριθμίζω όπως πριν
5)ln(e^2x+2)=x=lne^x ==> e^2x+2=e^x ονομάζω e^x=y και y²-y+2=0 η οποία δεν έχει λύση στο σύνολο των πραγματικών αριθμών.
ΥΓ Μήπως το +2 είναι -2? Τότε η λύση είναι y=2 ή y=-1 (απορρίπτεται) και e^x=2 λογαριθμίζω χ=ln2
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
250415
Νεοφερμένο μέλος


Έχω επισυνάψει το εξής αρχείο με τη λύσημπορει να βοηθησει κανεις στις παρακατω ασκησεις...??
....καθε υποδειξη ευπροσδεκτη..
View attachment Γενικά ισχύει.doc
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
vimaproto
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
250415
Νεοφερμένο μέλος


Στην άσκηση v ο εκθέτης είναι 2χ και όχι 2χ+2
ναι, έχεις δίκιο, δεν το είχα δει καλά. Τότε, όντως κι εμένα μου βγαίνει η Διακρίνουσα αρνητική, οπότε ή είναι κάποιο λάθος στην εκφώνηση, ή δεν έχει λύση.
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
MANOLIS_X3!!!
Νεοφερμένο μέλος


να προσδιορισετε το μεγαλυτερο ακεραιο ν ωστε ν^2 +2004ν να ειναι τελειο τετραγωνο ! ειναι απο διαγωνισμο τησ εμε ............ευχαριστω..
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
sokratis lyras
Νεοφερμένο μέλος


Παρακαλώ θα με βοηθήσετε με αυτήν:
να προσδιορισετε το μεγαλυτερο ακεραιο ν ωστε ν^2 +2004ν να ειναι τελειο τετραγωνο ! ειναι απο διαγωνισμο τησ εμε ............ευχαριστω..
k=n^2+2004n=(n+1002)^2-1002^2<(n+1002)^2.
Για k=(n+1001)^2 δεν έχουμε λύσεις ενώ για κ=(n+1000)^2 είναι n=250.000.
Με λίγα λόγια είναι αυτή https://www.mathematica.gr/forum/viewtopic.php?f=58&t=32268.
10Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
fAzR
Νεοφερμένο μέλος


παρακαλω αν μπορειτε να μου πειτε μετα πως γινεται με τις αλλεσ ριζες στον δευτερο τροπο.... ευχαριστω πολυ
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


όπου
Επειδή όμως η ανάλυση κάθε αριθμού σε γινόμενο πρώτων είναι μοναδική, ο εκθέτης του 2 στο δεξί μέλος θα είναι ίσος με τον αντίστοιχο εκθέτη του 2 στο αριστερό μέλος. Δηλαδή
άτοπο αφού οι
Επεξεργασία: Άλλαξα λίγο τον συμβολισμό για να είναι πιο σωστό
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
mary1269
Νεοφερμένο μέλος


f(x)=x-1/2x-1
Παίρνω την παραγωγο της συναρτησης και βγαινει 0.το λ θα ειναι ισο με το f'(2)=0
ποια θα εινια η εφαπτομενη?
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
nikoslarissa
Δραστήριο μέλος


H παραγωγος βγαινειΝα βρεθει η εφαπτομένη στο σημειο Α(2,f(2))
f(x)=x-1/2x-1
Παίρνω την παραγωγο της συναρτησης και βγαινει 0.το λ θα ειναι ισο με το f'(2)=0
ποια θα εινια η εφαπτομενη?
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Gareth
Δραστήριο μέλος


Να βρεθει η εφαπτομένη στο σημειο Α(2,f(2))
f(x)=x-1/2x-1
Παίρνω την παραγωγο της συναρτησης και βγαινει 0.το λ θα ειναι ισο με το f'(2)=0
ποια θα εινια η εφαπτομενη?
Αρχικά...f'(x)= [(x-1)/(2x-1)]'=(2x-1-2x+2)/(2x-1)^2=1/(2x-1)^2
Άρα f'(x)=1/(2x-1)^2
f(2)=1/3 ....f'(2)=1/9
άρα... η εφαπτομένη θα είναι: y-f(2)=f'(2)(x-2).....y-(1/3)=(1/9)(x-2).....y=x/9+1/3-2/9....y=x/9-1/9....y=(x-1)/9
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
giorgosHTML
Νεοφερμένο μέλος


Εχω καποιες για το φροντ. που παω εδω στη θεσαλλονικη.. θα ηθελα να μου πειτε καποια tips.. και γενικα ΜΕΘΟΔΟΛΟΓΙΑ για τη λυση ασκησεων στα πολυωνημα...
1η ασκηση) Να βρεθουν τα α,β (ανηκουν στο R) ωστε το πολυωνυμο p(x) = .... ax + b να διαιρειται ακριβως με το (χ+1)(χ-2) ..
Βασικα θελω τη μεθοδολογια γιαυτο δεν εδωσα και ολο το πολυωνυμο...
2η ασκηση) Αν το πολυωνυμο p(x) = ..... εχει για παραγοντα το χ^2 - 4 να δειχθει οτι 8β+γ+4α+5δ=0
Γενικα οι ασκησει που λενε να βρεθουν τα α,β ωστε.. πως τισ αντιμετωπιζω?
Ευχαριστω
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
vasilakis13
Δραστήριο μέλος


Αντί να διαιρείς κάθε φορά μπορείς να κάνεις διαδοχικά σχήματα horner. Στην πρώτη περίπτωση δηλαδή κάνεις πρώτα σχήμα horner με το χ+1 και στη συνέχεια κάνεις σχήμα horner στο δ(χ) που θα βρεις απο το πρώτο με το χ-2. Απαιτείς και τα 2 υπόλοιπα (απο το πρώτο horner και το δεύτερο) να είναι 0, δηλαδή οι συντελεστές, λύνεις το σύστημα κτλ...
Στη δεύτερη περίπτωση κάνεις ένα horner με το χ-2 και στο δ(χ) που θα βρεις κάνεις horner με το χ+2 και απαιτείς τα 2 υπόλοιπα να είναι 0...
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
giorgosHTML
Νεοφερμένο μέλος


σε αυτές τις ασκήσεις το βασικό στοιχείο που αξιοποιείς είναι ότι ένα άλλο πολυώνυμο είναι παράγοντας του βασικού σου πολυωνύμου. Για την πρώτη άσκηση λοιπόν διαιρείς το πολυώνυμο που σου δίνουν με το (χ+1)(χ-2) και μετά απαιτείς το υπόλοιπο της διαίρεσης να κάνει 0, αφού για να είναι παράγοντας πρέπει να κάνει 0. στο υπόλοιπο θα σου βγεί κάτι της μορφής κχ+λ=0 και επειδή το υπόλοιπο είναι κι αυτό πολυώνυμο πρέπει κ=0 και λ=0 (όπου κ και λ είναι μια σχέση με α και β). Το ίδιο πάνω κάτω κάνεις και στη δεύτερη, όπου θα διαιρέσεις το πολυώνυμο με το χ^2-4 και θα απαιτήσεις το πολυώνυμο του υπολοίπου να είναι 0, δηλαδή οι συντελεστές του να είναι 0 και θα λύσεις το σύστημα.
Αντί να διαιρείς κάθε φορά μπορείς να κάνεις διαδοχικά σχήματα horner. Στην πρώτη περίπτωση δηλαδή κάνεις πρώτα σχήμα horner με το χ+1 και στη συνέχεια κάνεις σχήμα horner στο δ(χ) που θα βρεις απο το πρώτο με το χ-2. Απαιτείς και τα 2 υπόλοιπα (απο το πρώτο horner και το δεύτερο) να είναι 0, δηλαδή οι συντελεστές, λύνεις το σύστημα κτλ...
Στη δεύτερη περίπτωση κάνεις ένα horner με το χ-2 και στο δ(χ) που θα βρεις κάνεις horner με το χ+2 και απαιτείς τα 2 υπόλοιπα να είναι 0...
Σε ευχαριστω πολυ.. σκεφτηκα να κανω τη διαιρεση αλλα δεν μου ηρθε στο μυαλο το αλλο βημα.. Διαδοχικα σχηματα horner θα προτιμησω μαλλον
 .. Αυριο μπορει να ποσταρω και καποιες αλλεσ ασκησεις σε περιπτωση που δεν τις καταφερω
.. Αυριο μπορει να ποσταρω και καποιες αλλεσ ασκησεις σε περιπτωση που δεν τις καταφερωΣημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
katerina_022
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


από κει και πέρα έχουν γίνει κάποια λογιστικά λάθη που δεν έχει νόημα να τα γράψω ένα ένα. Η σωστή σειρά μετά από το σημείο αυτό είναι
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Γατόπαρδος.
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
DumeNuke
Τιμώμενο Μέλος


Την συναρτηση f(x)=eφ(x/2) σε ποιο διαστημα τη σχεδιαζουμε;
Σχεδίασε την στο διάστημα (-π,π) και γράψε ότι είναι περιοδική, με περίοδο 2π.
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Γατόπαρδος.
Πολύ δραστήριο μέλος


Νομίζω
 \Rightarrow x \in (-\pi,\pi))
Γιατι ισχυει αυτο?
Σχεδίασε την στο διάστημα (-π,π) και γράψε ότι είναι περιοδική, με περίοδο 2π.
Πως αποδεικνυουμε την περιοδο μιας συναρτησης;
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 1 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 46 μέλη διάβασαν αυτό το θέμα:
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

