Βοήθεια/Απορίες στην Άλγεβρα

[kvgreco]

Αν

θετικοί πραγματικοί αριθμοί με

, να δείξετε ότι:

Μετά από πράξεις καταλήγουμε στην

ab+bc+ac >= 9abc

διαιρώντας με abc έχουμε να δείξουμε ότι (1/a)+(1/b)+(1/c) >= 9
πού είναι παρόμοια με μιά άσκηση την οποία είχε θέσει ο mostel παλιότερα.

Πού αποδεικνύεται με την ανισότητα cauchy

(a+b+c)/3 >= 3/[(1/a)+(1/b)+(1/c)]

Αποτελειώστε την βάζοντας a+b+c=1 καί κάντε χιαστί.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Dreamkiller]

Μετά από πράξεις καταλήγουμε στην

ab+bc+ac >= 9abc

διαιρώντας με abc έχουμε να δείξουμε ότι (1/a)+(1/b)+(1/c) >= 9
πού είναι παρόμοια με μιά άσκηση την οποία είχε θέσει ο mostel παλιότερα.

Πού αποδεικνύεται με την ανισότητα cauchy

(a+b+c)/3 >= 3/[(1/a)+(1/b)+(1/c)]

Αποτελειώστε την βάζοντας a+b+c=1 καί κάντε χιαστί.

Ναι, έτσι ακριβώς την έλυσα κι εγώ.
Το πρόβλημα όμως είναι ότι την βρήκα στο Internet ως άσκηση για παιδιά της Α' Λυκείου, η οποία δεν έχει στην ύλη βέβαια την ΑΜ - ΓΜ. Φανταζόμουν, λοιπόν, ότι λύνεται και με πιο εύκολο τρόπο και γι' αυτό την έβαλα. Όποιος τον βρει ας τον γράψει.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[kvgreco]

Ναι, έτσι ακριβώς την έλυσα κι εγώ.
Το πρόβλημα όμως είναι ότι την βρήκα στο Internet ως άσκηση για παιδιά της Α' Λυκείου, η οποία δεν έχει στην ύλη βέβαια την ΑΜ - ΓΜ. Φανταζόμουν, λοιπόν, ότι λύνεται και με πιο εύκολο τρόπο και γι' αυτό την έβαλα. Όποιος τον βρει ας τον γράψει.

Ναί εύκολο είναι,λόγω της a+b+c=1 η δοσμένη μετά καί από πράξεις γίνεται
(b+c)(a+c)(a+b) >=8abc
με πράξεις γίνεται

ba^2+ab^2+abc+cb^2+ca^2+abc+ac^2+bc^2 >=8abc

αλλά a^2+b^2 >= 2ab πολλαπλασιαζω με c>0 άρα ca^2+cb^2>=2abc (1) καί με όμοιο τρόπο θα πάρουμε ba^2+bc^2 >=2abc (2) καί ac^2+ab^2 >=2abc(3) καί με πρόσθεση κατά μέλη των τριών ανισοταυτοτήτων έχουμε ca^2+cb^2+ba^2+bc^2+ac^2+ab^2 >= 6abc καί προσθέτοντας καί στα δύο μέλη το 2abc έχουμε την αποδεικτέα!

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Ναυσικά]

ναι ομως βρε παιδια... το τετραγωνο πραγματικων αριθμων ειναι μεγαλυτερο απο το 0(θετικος αριθμος).
και εδω προκυπτει αθροισμα τετραγωνων πραγματικων αριθμων που
κανονικα επρεπε να ηταν μεγαλυτερο η ισο με το 0 και οχι μικροτερο!

μήπως έχεις βάλει στην εκφώνηση λάθος φορά???

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[nick_the_greek]

μήπως έχεις βάλει στην εκφώνηση λάθος φορά???

Για να ισχύει το <= θα πρέπει και οι δυο αριθμοί να είναι μηδέν. Επομένως ισχύει μόνο το ίσο αφού το μικρότερο δεν ισχύει για πραγματικό άριθμό.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Marizza92]

thnx
για όσους σεν ξέρουν για να βγει το ² πατάς το γράμμα ή τον αριθμό κ μετά ctrl-Alt κ το νούμερ 2²

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Dreamkiller]

Έστω σημείο Ο, εσωτερικό τριγώνου ABC. Να δείξετε ότι:



όπου t η ημιπερίμετρος του τριγώνου.

Btw, όποιος έχει καμιά καλή άσκηση Γεωμετρίας, ας τη βάλει.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[djimmakos]

Ορίστε μια ωραία ασκησούλα που θα κάψει "καρδιές" :p:
​

Nα παραγοντοποιηθεί η παράσταση:



Παίξτε μπάλα












































(Αν δω άτομο που θα κάνει τις πράξεις, θα χτυπήσω το κεφάλι μου στον τοίχο δις φορές)

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[who]

Ταυτότητα δεν είναι αυτό? Αν δεν κάνω λάθος κάνει .

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[djimmakos]

Ταυτότητα δεν είναι αυτό? Αν δεν κάνω λάθος κάνει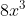

Σκάσε και άσε τα παιδιά να σκεφτούνε

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Shadowfax]

... εγώ γιατί θα έλεγα ότι γίνεται:

[(x+ψ) + (x-ψ)]^3

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Dreamkiller]

Τη γράφω γρήγορα γιατί ήδη έχω αργήσει και με περιμένουν.

Προσθαφαιρώ το 8x^3 να βγει Euler, βγάζω κοινό παράγοντα το 3(χ-y)(x+y), η παρένθεση βγαίνει 0 και μένει το 8χ^3.

Θα τη γράψω αναλυτικά το βράδι.

ΥΓ: Τώρα που είδα τις απαντήσεις νιώθω λίγο χαζούλης.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[djimmakos]

... εγώ γιατί θα έλεγα ότι γίνεται:

[(x+ψ) + (x-ψ)]^3

Αυτό είναι και βγαίνει 8x^3 αλλά είπα στον who έτσι γιατί μπαίνει στα θέματα Α' λυκείου ενώ είναι ολόκληρος φοιτητής

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[etrygeom]

Έστω σημείο Ο, εσωτερικό τριγώνου ABC. Να δείξετε ότι:



όπου t η ημιπερίμετρος του τριγώνου.

Btw, όποιος έχει καμιά καλή άσκηση Γεωμετρίας, ας τη βάλει.

Έχουμε:

Τριγωνική ανισότητα για τη κάθε πλευρά χωριστά: και

Οπότε:

Η πρώτη ανισοτική σχέση δεν μου κάνει κούκου αυτή τη στιγμή. Την αφήνω σε άλλον.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[kvgreco]

Η πρώτη ανισοτική σχέση δεν μου κάνει κούκου αυτή τη στιγμή. Την αφήνω σε άλλον.

Προσπάθησε να δείξεις ότι ΟΒ+ΟΓ< ΑΒ+ΑΓ (1)(Είναι πολύ χρήσιμο αυτό γενικώς σε τέτοιες ασκήσεις πού αναφέρονται σε εσωτερικό σημείο τριγώνου)
Αφού το δείξεις αυτό, άρα ομοίως θα ισχύει ΟΑ+ΟΓ < ΒΑ+ΒΓ(2) καί ομοίως ΟΑ+ΟΒ < ΓΑ+ΓΒ (3).
Με πρόσθεση κατά μέλη των τριών ανισοτήτων προκύπτει το ζητούμενο.

Το θέμα είναι επομένως να αποδείξεις μιά από τις τρείς.Γιά βοήθεια σού λέω αν θές να αποδείξεις την (1) να προεκτείνεις την ΟΑ μέχρι να τμήσει την ΒΓ σε κάποιο σημείο Δ καί εκεί παίρνεις δύο φορές την τριγωνική (με το άθροισμα) σε δύο τριγωνάκια πού δημιουργούνται καί με πρόσθεση κατά μέλη των δύο ανισοτήτων πού προκύπτουν δείχνεις την (1).
Είναι αργά καί είμαι σε μιά κατάσταση νύστας. Την πέφτω καληνύχτα!

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[delirium]

γελειο ειναι ρε παιδια...!!! )

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Dreamkiller]

Για την αρίθμηση των σελίδων του Λεξικού της Νέας Ελληνικής Γλώσσας του καθηγητή Γ. Μπαμπινιώτη (Β' Έκδοση) χρειάστηκαν συνολικά 7149 ψηφία. Πόσες σελίδες έχει το λεξικό;

[Από το βιβλίο "Ολυμπιάδες Μαθηματικών - Μαθηματικοί Διαγωνισμοί για τη Β' Γυμνασίου", του Μπάμπη Στεργίου, εκδόσεις Σαββάλας].

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[djimmakos]

Για την αρίθμηση των σελίδων του Λεξικού της Νέας Ελληνικής Γλώσσας του καθηγητή Γ. Μπαμπινιώτη (Β' Έκδοση) χρειάστηκαν συνολικά 7149 ψηφία. Πόσες σελίδες έχει το λεξικό;

[Από το βιβλίο "Ολυμπιάδες Μαθηματικών - Μαθηματικοί Διαγωνισμοί για τη Β' Γυμνασίου", του Μπάμπη Στεργίου, εκδόσεις Σαββάλας].

Επειδή τυχαίνει να το έχω το λεξικό αυτό δε λέω τη λύση για να το ψάξουν και οι άλλοι

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Ίρις]

Πάντως όσους ενδιαφερει : γίνεται μαθηματικός διαγωνισμος καθε χρονο. Κάθε χρόνο πηγαινω καθε χρονο δεν παιρναω στην επόμενη φαση, Αξιζει τον κόπο:no1:
-----------------------------------------
Και αμα θέλετε άσκηση να χτυπάτε το κεφάλι σας στον τοιχο(μου την εδωσε ο μαθηματικος μου γιατι με εβλεπε πολυ καλη) : να αποδειξετε οτι ενα τριγωνο ειναι ισοσκελες αν και μονο αν 2 διαμεσοι του ειναι ισες. (χρειαζεται βοηθητικο σχημα και συνδιαζει και θαλη απο περσυ)

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[thewatcher]

2064

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.