Το πρώτο τριώνυμο παίρνει ελάχιστη τιμή τον 2 καί μάλιστα γιά χ=1 πού είναι καί προφανής λύση της εξισωσης.Το άλλο τριώνυμο υψωμένο κι αυτό σε άρτιο καί αφού έχει καί ρίζες θα δίνει τιμές (ως δύναμη), > = 0.
Δηλαδή ο πρώτος όρος δίνει τιμή 2^2004 γιά χ=1, ταυτόχρονα ο δεύτερος δίνει 0 άρα επαληθεύεται η εξίσωση.Γιά οποιονδήποτε άλλον χ οι δύο πρώτοι όροι δίνουν αθροιστικά αριθμό μεγαλύτερο από 2^2004.
Συμπεραίνουμε ότι η εξίσωση έχει μοναδική ρίζα τον χ=1.
Σωστος εισαι. Ας τη γραψω και σε latex για να φαινεται καλυτερα
}^{2004}={({(x-1)}^{2}+2)}^{2004}\geq{2}^{2004})
Η ισοτητα ισχύει για x=1
Δηλαδη
}^{2004}\geq{2}^{2004})
Με την ισοτητα για να ισχύει αν και μονο αν x=1 (Σχεση 1)
}^{2004}={[(x-1)(x-2)]}^{2004}\geq0)
Η ισοτητα ισχύει για x=1 ή x=2 (Σχεση 2)
Δηλαδη
}^{2004}\geq0)
Με την ισοτητα να ισχύει αν και μονο αν x=1 ή x=2 (Σχεση 2)
Με προσθεση των (1),(2) κατα μελη εχουμε οτι
}^{2004}+{({x}^{2}-3x+2)}^{2004}\geq{2}^{2004})
Ισοδυναμα
}^{2004}+{({x}^{2}-3x+2)}^{2004}-{2}^{2004}\geq0)
H ισοτητα ισχύει οταν ισχύουν ταυτοχρονα οι ισοτητες στις (1) και (2)
Αρα οταν x=1
Να ρωτήσω κάτι? Επειδή εδώ είναι το μέρος γιά την Α Λυκείου μήπως δεν είναι σωστό να γράφουμε εμείς οι μαθητές άλλων τάξεων?
Οταν οι ασκησεις ειναι απλες πχ να λυθει μια εξισωση 1ου,2ου βαθμου η να αποδειχθει μια ταυτοτητα καλο ειναι να αφηνουμε τα παιδια της α να προσπαθουν μονα τους. Τωρα για περιεργες ασκησεις αν δε τα καταφερνουν καλο ειναι να τους δινουμε τη λυση απο παρομοιες ωστε να εξοικειωθουν με αυτου του ειδους τις ασκησεις η να τους δειχνουμε προς τα που να κινηθουν με καποια υποδειξη κλπ. Οι καθηγητες του forum τα ξερουν καλυτερα αυτα.
(Τι τόθελα το τελευταίο μπάνιο μέσα στο κρύο.Παιδιά έχω αρπάξει τρελό κρυολόγημα πριν καλά καλά ανοίξει το σχολείο.Δέχομαι τα.. περαστικά σας!


)
Περαστικα!
-----------------------------------------
Ασκηση 2
Να απλοποιηθεί η παράσταση:
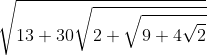
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.



Στο λατεξ θελω να μαθω ποιο είναι βρε


 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki


 )
)

